








ОСОБЕННОСТИ ФОРМИРОВАНИЯ МАТРИЦ ФИЗИКО-МЕХАНИЧЕСКИХ, ТЕПЛОФИЗИЧЕСКИХ И ДРУГИХ СВОЙСТВ, В УСЛОВИЯХ ВОЗМОЖНОГО ИЗМЕНЕНИЯ ПАРАМЕТРОВ.
Распределение свойств в точках интегрирования элементов различного вида.
Метод конечных элементов представляет собой эффективный численный метод решения инженерных и физических задач. Область его применения простирается от анализа напряжений в конструкциях самолетов или автомобилей до расчета таких сложных систем, как атомная электростанция. С его помощью рассматривается движение жидкости по трубам, через плотины, в пористых средах, исследуется течение сжимаемого газа, решаются задачи электростатики и смазки, анализируется колебания систем.
Основная идея метода конечных элементов состоит в том, что любую непрерывную величину, такую, как температура, давление и перемещение можно аппроксимировать дискретной моделью, которая строится на множестве кусочно-непрерывных функций, определенных на конечном числе подобластей. Кусочно-непрерывные функции определяются с помощью значений непрерывной величины в конечном числе точек рассматриваемой области.
Чтобы показать, как определяются матрицы элементов и каким образом с их помощью формируется система линейных уравнений, рассмотрим стержень с поперечным сечением в форме квадрата (рис 1а). В связи с наличием четырех осей симметрии можно рассмотреть только 1/8 квадрата. Разобьем эту часть на четыре элемента, как показано на рис. 1б. Четырех элементов мало для получения приемлемой точности решения, но вполне достаточно для иллюстрации техники получения необходимой системы уравнений, что является нашей целью.
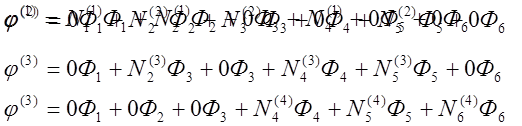 |
|||
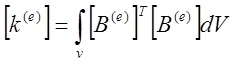 |
![]()
![]()
Здесь учтено, что в
рассматриваемом случае:
Для определения необходимо дифференцировать по Х и Y.
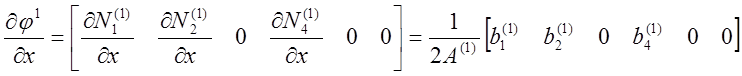 |
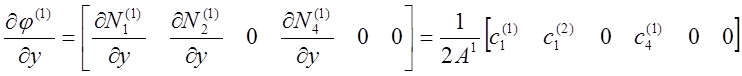 |
|||
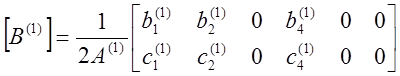 |
|||||
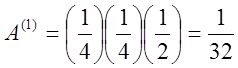 Площадь этого элемента:
Площадь этого элемента:
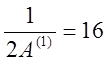 и
и
Коэффициенты b и с равны
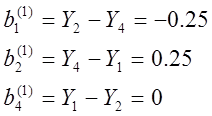 |
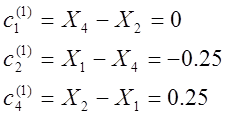 |
Подставляя эти значения в формулу (3), получаем
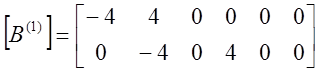 |
|||
Произведение равно
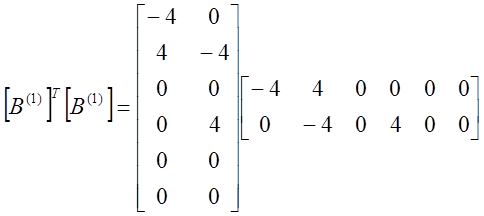 |
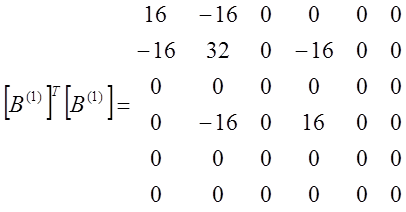 |
![]()
![]()
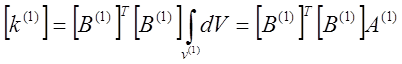 |
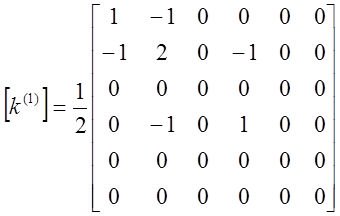 |
Объемный интеграл
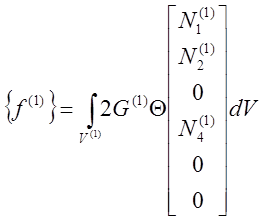 |
вычисляется просто, если воспользоваться системой L-координат:
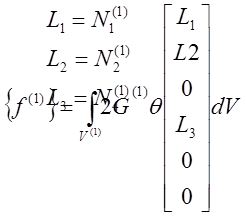 |
Предполагая толщину элемента единичной и применяя интегральную формулу
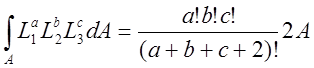 |
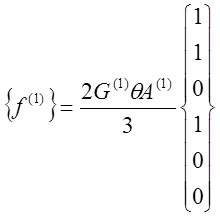 |
|||
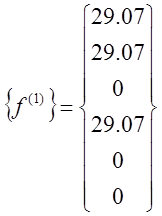 Подстановка значений
Подстановка значений
![]()
![]() дает
дает
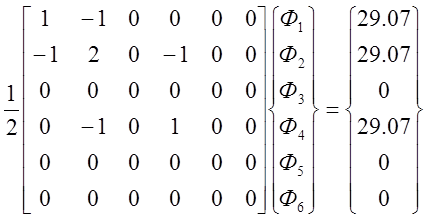 |
Аналогично можно получить систему уравнений для любого другого элемента. Окончательное выражение для матриц остальных элементов выглядят:
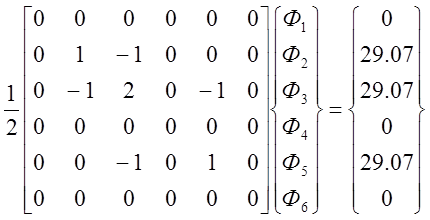 |
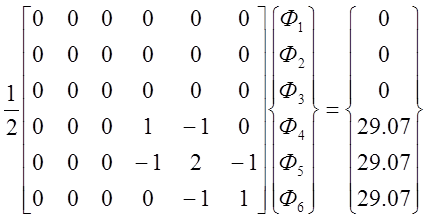 |
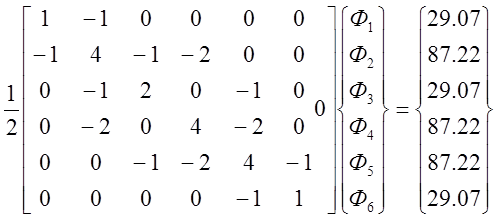 |
|||
Все величины Ф с индексами 3, 5, 6 равны нулю, так как соответствующие им узлы расположены на внешней на внешней границе. Преобразуя систему уравнений (12) и решая ее, получаем
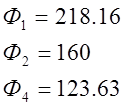 |
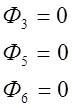 |
||||||
Уравнение теплопроводности в сплошной среде имеет вид
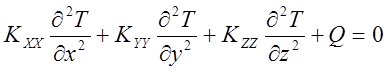 |
|||
Где Т- температура; К- коэффициенты теплопроводности в направлениях X, Y и Z размерности кВт/м*К; Q- источник тепла внутри тела, который считается положительным, если тепло подводится к телу, его размерность кВт/м**3.
С уравнением (13) связывают два вида граничных условий. Если температура известна на некоторой части границы, то пишут
![]() Где
Где
поверхности s. Если на границе происходит конвективный теплообмен, который характеризуется величиной h, или задан поток тепла q, то граничное условие имеет вид
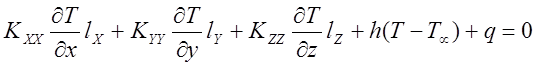 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.