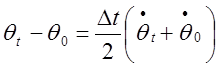Уравнения параболического типа, теория диффузии и практическое составление матрицы инерции четырехугольного элемента с использованием метода редукции, страница 3

                                                                                                   (27)  

где -неизвестные значения величин в конце шага ; -известные начальные значения.

Подставляя значение  из выражения (27  ) в уравнение (26),

записанное для t = получаем

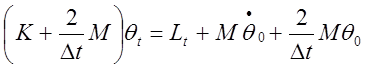              (28)

Используя равенство (26  ) при t =  из выражения    (28) находим следующую рекуррентную формулу для последовательного пошагового определения неизвестной функции :

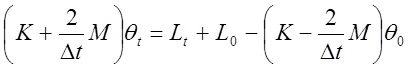         (29)

 Для установившегося режима интегрирование проводить не нужно ,так как тогда выражение (26  ) приводится просто к уравнению

 Так как явление  теплопроводности есть диффузионный процесс, приведенные выше формулы и уравнения теплопроводности  выглядят идентично. Например, может быть использовано выражение для потока тепла

 ,

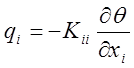где — количество тепла, протекающего через единицу площади, перпендикулярной к  направлению  (кал, Дж и т. д.);  — коэффициент теплопроводности в направлении ,  — температура.

2.3. Задачи диффузии и конвенции

При совместном рассмотрении диффузии и конвекции необходимо решить систему уравнений (25  ), записанную, как обычно, в эйлеровых координатах. Решение можно получить интегрированием по времени указанной системы  Решение состоит в комбинации систем координат Эйлера и Лагранжа. Эйлерова сетка конечных элементов допускает произвольные искривления, но в вычислительном отношении очень неэффективна из-за наличия конвективных членов, содержащихся в несимметричной матрице А уравнений (25). Наоборот, если используется схема Лагранжа при изучении движения жидкости, то сетку элементов легко можно сделать очень искривленной. Представляется удобным  для такого типа задач применять смешанную эйлерово-лагранжеву схему. При этом будет выполняться простое интегрирование, присущее формулировке Лагранжа, но сохранится вычислительная сетка, используемая в схеме Эйлера.

Для схемы Лагранжа (при отсутствии конвективных членов) можно получить рекуррентное соотношение, аналогичное выражению (29  ). Для введения конвекции в это уравнение, характеризующее нестационарный режим, во многих задачах диффузии можно предположить, что для малого  диффузия не зависит от конвекции и матрицы в уравнении (29  ) постоянны. Конвекция впоследствии вычисляется в предположении, что в каждом элементе находится фиксированная масса жидкости, и ее движения определяются в пределах временного шага по распределению скорости.

   В этом случае величина , обусловленная как диффузией, так и конвекцией, известна в ряде точек новой сетки. Значения концентрации в точках первоначальной сетки могут быть вычислены по значениям  новой сетки интерполяцией. Процедур интегрирования можно повторить для следующего шага по вре-

мени.

  Таким образом, в данной схеме считается, что элемент движется вместе с жидкостью, когда рассматривается конвективная часть, но при рассмотрении диффузии элемент остается в том же  самом положении в пространстве, а жидкость проходит через него.

2.3.  Нелинейная диффузия

    Во многих задачах диффузии константы диффузии зависят от значений функции концентрации. Поэтому такие задачи являются нелинейными. Для примера уравнение, характеризующее установившуюся неконвективную диффузию:

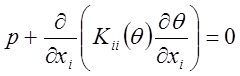,                                 (30)

где коэффициенты   являются функциями .

После применения процедуры метода конечных элементов получим нелинейную систему уравнений типа

                         (31)

Для решения системы (31 ) начнем с начальной величины   и  найдем улучшенное приближение . Рекуррентное соотношение при этом записывается :

                                                                                                               (32)                                      

Можно ускорить сходимость решения, используя метод Ньютона — Рафсона. В этом случае определяют невязку по результатам 1-й аппроксимации:

.               (33)

Накладывают  условие

                                    (34)

Это дает рекуррентное соотношение         

где                                                          (35)

                       (36)

Из уравнения (36)  можно найти . Таким образом,

                                 (37)

Степень сходимости решения в данном случае имеет второй порядок.

5. Литература

1. Сегерлинд Л.Д. “Применение метода конечных элементов” -М.: Мир, 1979.

2. Галлагер  “Основы  в  методах  конечных  элементов“.

3. Коннор и Бреббиа “Метод конечных элементов в жидкости“, 1979.