Математика \ Основы метода конечных элементов

Изучение безвихревого течения идеальной жидкости, страница 2

       ]   

2.1.4. Соотношения, определяющие элементы

  Чтобы получить соотношения, определяющие элемент, необходимо вычислить объемные и поверхностные интегралы:

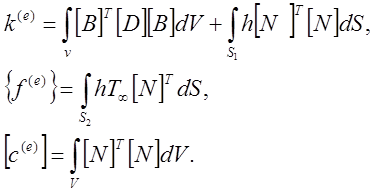(2.8)

Замену переменных интегрирования можно сделать с помощью соотношения

    (2.9)

где t ¾ толщина элемента. Объемные интегралы в () приводятся к виду

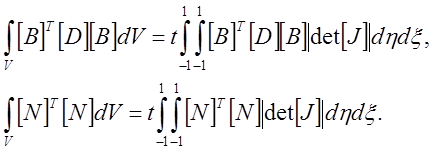(2.10)

Переход к переменным интегрирования x и h упрощает пределы интегрирования, что позволяет избежать трудностей, возникающих, при рассмотрении элементов с криволинейными границами.

  Объемные интегралы в (2.10) записываются в общем виде следующим образом:

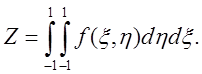      (2.11)

Этот интеграл может быть определен численно: сначала вычисляется внутренний интеграл, в котором x считается постоянной, а затем вычисляется внешний интеграл. Вычисление внутреннего интеграла дает

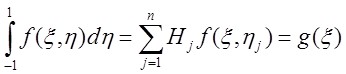,  (2.12)

где g(x) — функция от x. Внешний интеграл теперь записывается в виде

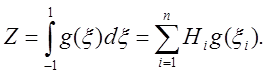         (2.13)

Последнее выражение после подстановки g(x) по формуле (2.12) принимает вид

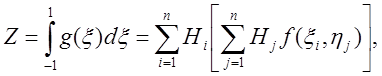
или

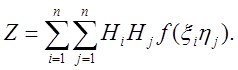  (2.14)

Порядок квадратурных формул, требуемый для точного вычисления объемных интегралов, дан в табл. 2.1.

                                                                                                                        Таблица 2.1.

Порядок квадратур Гаусса ¾ Лежандра для двумерных элементов

Элемент

       [N]T[N]

       [B]T[B]

      [N]T

          x,h

         x,h

x,h

Линейный

          2,2

         2,2

      1,1

Квадратичный

          3,3

         2,2

      2,2

Кубичный

          4,4

         3,3

      2,2

Для определения матриц элемента в случае для кубичного четырехугольника требуется 16 точек интегрирования. Эти точки интегрирования располагаются по элементу симметрично. Расположение точек для кубичного элемента показано на рис. 2.2.

  Применение формул (2.14) требует большого объема вычислений.

  Для составления матриц элемента в (2.8) необходимо определить два поверхностных интеграла:

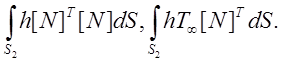  (2.15)

Вычисление этих интегралов является относительно простой операцией, если элемент ограничен прямолинейными сторонами, но становится более сложным в случае криволинейных сторон .

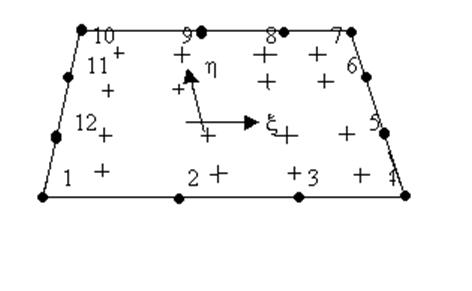
Рис.2.2. Точки интегрирования кубичного элемента.

  Если стороны элемента прямолинейные, проще всего интегралы в (2.15) вычисляются аналитически. После вычисления коэффициентов матриц они могут быть сохранены в машинной памяти для дальнейшего использования.

2.1.5.Расчёт значений матрицы жесткости конечного двенадцати-узлового элемента.

Решение основного уравнения:

можно записать в виде:

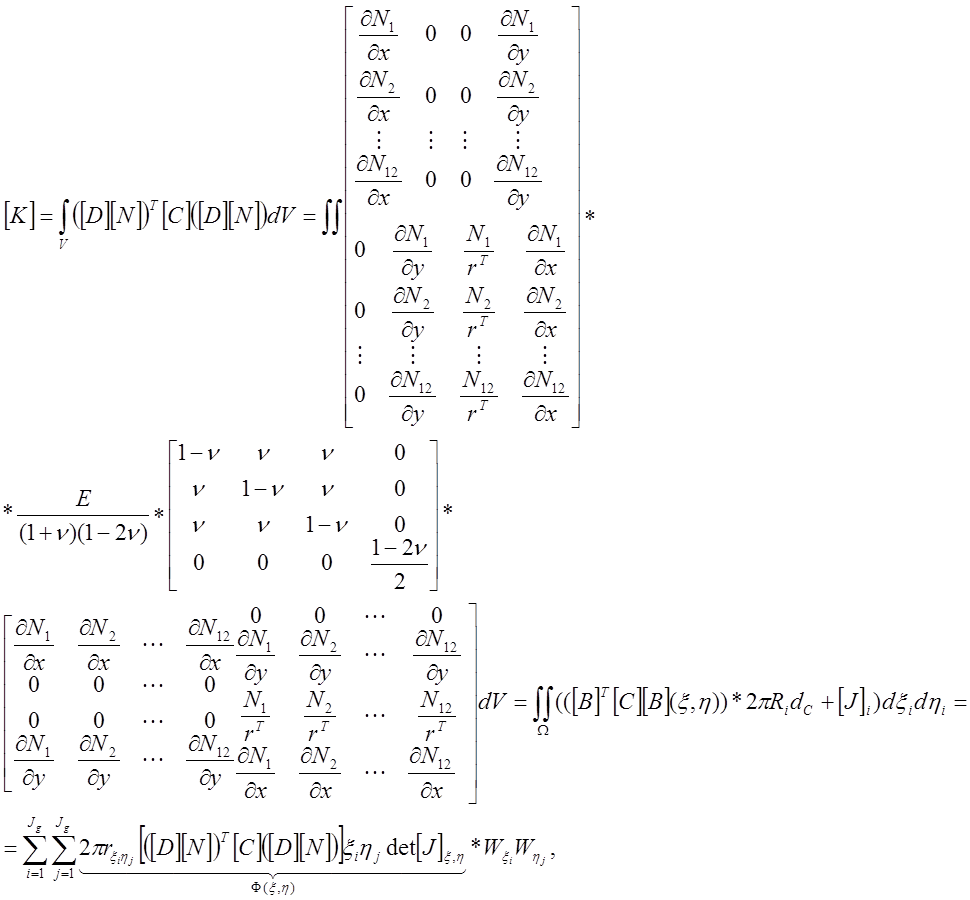
где Wxi, Whj ¾ весовые коэффициенты,

        rx,h ¾ радиус точки интегрирования,

         F(x,h) ¾ функция интегрирования в точках с координатами xi, hj.

Полный расчёт значений матрицы коэффициентов жесткости конечного двенадцатиузлового элемента состоит из суммирования подынтегрального выражения по точкам интегрирования для каждой локальной координаты xi и hj.

2.1.6. Напряжение в точке интегрирования.

     Напряжение в каждой точке интегрирования определяется по соотношению:

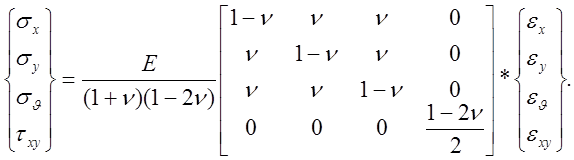
2.1.7. Вектора нагрузок.

   Вектор нагрузок, образующийся в следствие начальных деформаций, можно определить по соотношению вида

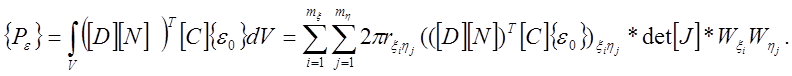
  Вектор поверхностных нагрузок определяется по формуле

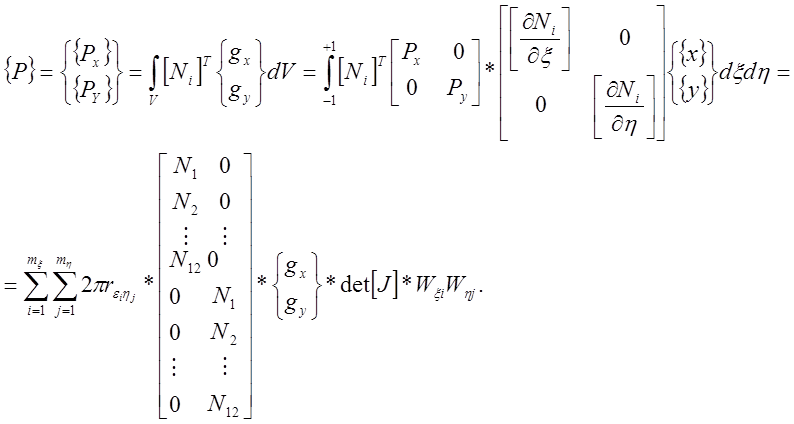
2.2. Решение системы линейных уравнений с итерационным уточнением

 Подпрограмма RSLMC с обычной точностью. Эта подпрограмма предназначена для решения системы линейных уравнений вида

AC=B,

где A ¾ неособенная матрица коэффициентов системы; B ¾ вектор правых частей.

  Матрица A представляется в виде произведения треугольных матриц следующим образом:

RA=LU,

где L ¾ нижняя треугольная матрица с единичной диагональю; U ¾ верхняя треугольная матрица; P ¾ матрица перестановок.

  Введением обозначения C=P*B исходная система приводится к виду

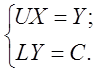
   Решение системы находим путём итерационного уточнения приближенного решения, найденного методом исключения Гаусса.

   Уточнённое решение X(p+1) получается из приближённого решения X(p) следующим образом.

   Сначала вычисляется вектор невязки

r(p)=B-AX(p).

   Затем, решая систему

Ad(p)=r(p)

 с использованием LU¾разложения матрицы A, получаем вектор поправки d(p).

    Наконец, поправка прибавляется к X(p), что даёт уточнённое решение:

X(p+1)=X(p)+d(p).

    Эти три шага повторяются до получения заданной точности, начиная с X(0)=0.

    Итерационный процесс оканчивается при появлении одной из следующих ситуаций:

Скачать файл