Напряженно-деформированное состояние сплошной среды. Функции формы квадратичных элементов, страница 2

Тепловой баланс тела в произвольный момент времени с учё­том аппроксимации его объёма и теплофизических параметров опи­сывается системой обыкновенных дифференциальных уравнений пер­вого порядка

С+ КТ + F  =0  (1.6)

или

[С]+ [К]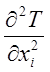 + {Q}_v+{a_i()}_S1 +{q_j}_S2 ={0}   при {T_s}  наS₃,

где:  [С], С   - матрица характеристик теплоёмкости и теплопроводности [К], К ;

        {Q_V} - вектор столбец нагрузок вызванных внутренними теплоисточниками в объёмеV;

и соответственно  {a_i()}_S1 , теплоотдачей на S₁ ;   {Q_J)}_S2 - теплопотоками на S₂;  {T_e}_S3   - температурой на S₃ и n - число неизвестных или порядок системы.

При рассмотрении задачи нестационарной теплопроводности каждый элемент объёма тела V_K обладает конкретными теплофизическими свойствами:

-  теплопроводностью l(вт/(см×град); 

-   – теплоёмкостью (дж/(см³×град) и имеет внутренние теплопотоки Q_K  (вт/см³).

На поверхности S₁ происходит конвективный теплообмен интенсивностью a_i(), где a_i - коэффициент теплоотдачи температуры средой стенке /поверхности/ тела (вт/см²×град),  - температура среды омывающей эту поверхность (С°, град). На поверхностиS₂ действуют теплопото­ки q_J (вт/см²) тоже приводящие к изменению температуры  в объеме тела, а на отдельных участках поверхности тела S₃ тем­пература задана Т_s и характер изменения ее во времени известен.

Заметим, что выбранная дискретизация исследуемого объема среды при рассмотрении различных физических задач остается в основном неизменной, что говорит об ее универсальности. Понятно, что индексация объемов и поверхностей, показанная здесь одинаковым обозначением, на самом деле не совпадает при решении различных задач. Это обусловлено тем, что физические процессы, как например, охлаждение за счет теплоотвода и нагружение от сосредоточенных сил происходят в разных областях. 

2.3 ПРОСТРАНСТВЕНАЯ ДИСКРЕТИЗАЦИЯ ОСЕСИММЕТРИЧНОЙ ЗАДАЧИ

МЕТОДОМ КОНЕЧНЫХ ЭЛЕМЕНТОВ

Проблема определения экстремальных уровней градиентов в неравномерно-распределённых полях  параметрических состояний сплошной среды или физически неоднородных  конструкций, изготов­ленных из сплошных материалов и имеющих сложную геометрическую Форму, в большинстве случаев решается на основе привлечения дискретных моделей.

Используемый элемент в изогнутом пространстве точно интег­рируется по количеству точек равному 8, 21, 27 /20 узлов/, а в плоскости 4, 9/8 узлов/. Такое соответствие 9:8, 21:20 создаёт предпосылки сравнительно точного учёта характера распределения в оплошной среде переменных искомых функций. Кроме того элемент сравнительно прост при аксонометрическом построении составных сложных тели их поверхностей, легко изменяется в пространстве и при некоторой доработке может описывать как  объём тела боль­шой протяженности так и тонкие оболочки.

2.4. ФУНКЦИИ  ФОРМЫ  КВАДРАТИЧНЫХ ЭЛЕМЕНТОВ

В данной разработке в качестве базового изпараметрический  8-узловой элемент в котором непрерывность интересуемых параметров создается с помощью квадратичных функций (рис. 2), описанных ранее.

Базовый элемент

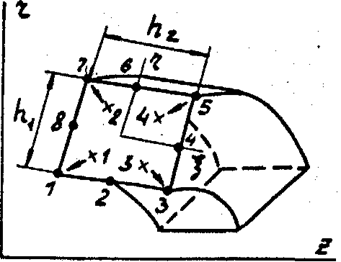
Рис. 2. .

В целях сокращения затрат машинного времени при задании геометрии квадратичного элемента в общей системе координат применяются эти же функции. Таким образом, элемент является изопараметрическим, сирендипова семей­ства.

3. Последовательность создания алгоритма

Последовательность создания алгоритма можно поэтапно представить так:

1) Создание  подпрограммы формирования матрицы жесткости исследуемой области

2) Создание подпрограммы формирования вектора нагрузок

3) Создание подпрограммы учета граничных условий

4) Решение системы  линейных уравнений

5) Переход от полученного решения к факторам напряженно-деформированного состояния исследуемой области

Самым емким этапом в работе было создание подпрограммы матрицы жесткости системы, поэтому, считаю наиболее целесообразным, подробно рассмотреть именно эту часть алгоритма программы.

Алгоритм  определения  матрицы жесткости.

1.0 Начало

2.0 Чтение данных из исходных файлов (количество конечных элементов разбивки исследуемой области, количество узлов области, их координаты, механические характеристики области, данные нагрузки, граничные условия)

3.0 Выделение машинной памяти под решение задачи (имеется в виду динамическая память, как наиболее эффективный инструмент при решении заранее не определенных по объему задач)

4.0  Цикл по всем элементам