2. МЕТОДИКА ИССЛЕДОВАНИЯ ПОТЕРИ УСТОЙЧИВОСТИ
ЭЛЕМЕНТА КОНСТРУКЦИИ АМОРТИЗАТОРА
2.1. Метод конечных элементов
Во многих случаях точное описание исследуемого пространства, занимаемого фрагментом конструкции возможно только объединением совокупности элементов- “кирпичиков“ разных конфигураций пространства. Их существует ряд разновидностей: симплекс-, комплекс- и мультиплекс – элементы [2.1]. В данном случае используется полином комплекс–элемента, включающий члены второго порядка.
2.1.1. Модели элементов высокого порядка
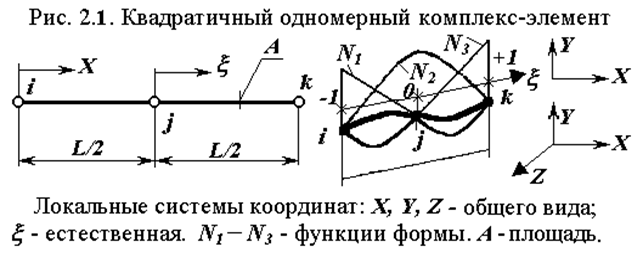
Элементы высокого порядка (Рис. 2.1, рис. 1.3) позволяют получать более точные результаты. Рассмотрим применение элементов такого порядка, с полиномиальной функций общего вида, зависящей от одной переменной для одномерного элемента можно представить выражением
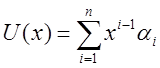 , (2.1)
, (2.1)
где i—число узлов (или степеней свободы) элемента.
Например, криволинейному элементу с тремя узлами (один узел расположен посередине между крайними узлами, рис. 2.2) соответствует интерполяционный полином
j=a1+a2 x+a3 x2 ,
где a1, a2, a3 определяются из условий для узловых точек, подставляя которые, находят функции формы
N1=(1-
2x/L)(1- x/L), N2=![]() (1- x/L), N3= –
(1- x/L), N3= –![]() (1- 2x/L)
. (2.2)
(1- 2x/L)
. (2.2)
2.1.2. Преобразования координат. Матрица Якоби
Чтобы более полно описать вид описываемого геометрического фрагмента конструкции используется специальное преобразование с введением естественной системы координат. При этом, локальной (естественной) системой координат для одномерного элемента является относительная длина, определяемая как -1 £x£ 1, где x - координата. Начало отсчета по xчаще всего выбирается в средней точке элемента. Используемые функции вида
x=f(x) и, наоборот, x =g(x) (2.3)
предполагаются взаимно однозначными. Например, для квадратичного (рис.2.2) элемента
Ni=![]() (1-x), Nj=(1+ x )(1-x ), Nk=
(1-x), Nj=(1+ x )(1-x ), Nk=![]() (1+ x)
. (2.4)
(1+ x)
. (2.4)
Переход к новой координатной системе X выполняется также по этой же стандартной формуле
x=Nb iXi+Nb jXj+Nb kXk=[Nb]{X},
однако входящие в уравнение функции Nb i(xТ) могут быть уже другими, тоже зависящими от локальных координат x, согласно (2.1).
Вычисление производных по координатным осям X, Y, Z выполняется по отношению
d[Nb]/dx=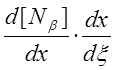 , откуда d[Nb]/dx=
, откуда d[Nb]/dx=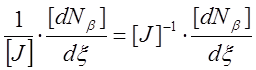 . (2.5)
. (2.5)
Введенный новый параметр [J]=Jx=dx/dx=d([Nb]{X})/dx= =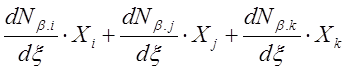 или [J]=d([Nb]/dx)× {X}=
или [J]=d([Nb]/dx)× {X}=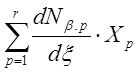 , (2.6)
, (2.6)
обозначает так называемую матрицу Якоби, связывающую локальные значения координат с глобальными. Здесь p это номер функции Nb, а также и номер узла, в котором эта функция Nb.p=1, во всех остальных узлах (их число равно r) значение функции равно нулю.
2.1.3. Соотношения, определяющие элементы
Во многих случаях приходится вычислять объемные и поверхностные интегралы различных видов. Прежде чем перейти к их рассмотрению, освоим более простой расчет самих объемов, боковой либо другой поверхности, который, надо сказать, выполняется для высокоточных элементов несколько по иному. Так, элементарный объем стержневого элемента с площадью поперечного сечения, равной А, в обычной системе координат по X определяемый как dV=Аdх, запишется уже в виде
![]()
в двухмерной (X, Y) и трехмерной системах (X, Y,Z) формула расчета не изменится, однако якобиан [J] и его определитель det[J], согласно (2.6), будет уже другим. Боковая поверхность определяется подобным же образом
![]() ,
,
где Lx(x) — длина боковой окружности поперечного сечения.
В свою очередь текущие значения координат x.i элемента в глобальных осях обусловлены значениями локальных осей x.i, то есть x.i(x1,x2,x3)= =[Nb.L(x1,x2,x3)]{X L.i }=xb.i, где Nb.L – функция геометрической формы элемента в узле L, а {X L.i } координаты узлов.
Объем одномерного криволинейного элемента с переменной площадью поперечного сечения A(x) в любом координатном пространстве в естественной локальной системе с осью xравен
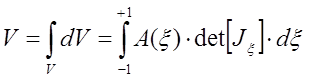 .
.
Ввиду того, что входящие в подынтегральные выражения функции являются сложными, выполняется численное интегрирование
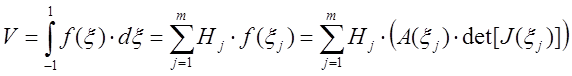 ,
,
где Нj — весовые коэффициенты, а f(xj) — подынтегральная функция.
Объем области в трехмерном пространстве составляет
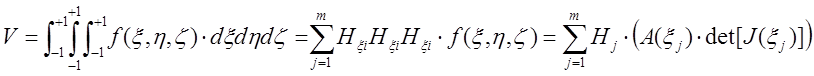 (2.7)
(2.7)
Рассмотренные выражения для расчетов площади либо объема элементов позволяют без особых проблем вычислять интегралы, определяющие основные уравнения метода конечных элементов, вида
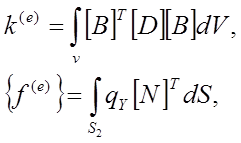 (2.8)
(2.8)
которые, собственно, и формируют решаемую систему уравнений
[K] {D}={P} . (2.9)
Существенным отличием высокоточных элементов от линейных, является возможность задания более точно свойств материалов среды. Подынтегральные функции, зависящие от переменных локальных координат x,h, z могут описывать в пределах пространства элемента его общие характеристики, такие как неравномерные свойства материала, объемной нагрузки и другие.
2.1. Оден Дж. Конечные элементы в нелинейной механике сплошных сред. –М.: Мир, 1997. С.431.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.