Найдем все маршруты длины 2, выходящие из вершины 1. Для их нахождения будем последовательно перебирать маршруты, проходящие через смежные с 1 вершины: 4, 5, 6, 8. Через смежную вершину 2 маршрутов длины 2 не существует. Запишем их как последовательности смежных вершин: 143; 156; 157; 158; 165; 167; 168; 185; 186; 187.
Найдем все простые циклы, содержащие вершину 1. Для простоты нахождения будем считать, что цикл выходит и заканчивается в вершине 1. Последовательно перебирая все маршруты, в порядке возрастания номеров вершин, выходящие и заканчивающиеся в вершине 1, получаем следующий список: 1561; 156781; 15681; 15761; 157681; 15781; 1581; 15861; 16781; 1681.
Данный граф является связным, поскольку из его диаграммы очевидно, что любая пара его вершин соединяется цепью.
Найдем все степени вершин графа. Для этого найдем число ребер, инцидентных данной вершине. Запишем результат в виде таблицы.
|
Номер вершины |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Степень вершины |
5 |
1 |
1 |
2 |
4 |
4 |
3 |
4 |
Поскольку в графе есть вершины, степени которых нечетны, например, вершина 1, то данный граф не является эйлеровым.
Найдем остов графа. Поскольку вершины 1, 2, 3, 4 не образуют цикла, то они войдут в остов со всеми соединяющими его ребрами. Рассмотрим первый цикл из списка циклов 1561. Поскольку в остове графа не должно содержаться циклов, то удалим в графе произвольное ребро, входящее в данный цикл, например, ребро l7, соединяющее вершины 5 и 6. Диаграмма графа будет выглядеть так:
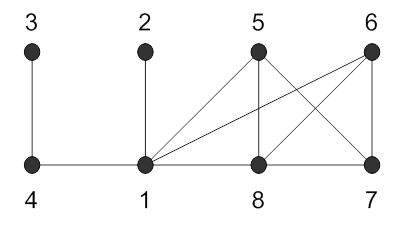
Найдем следующий цикл из списка, не содержащий ребро l7.: 15761. Удалим из графа ребро l10, соединяющее вершины 6 и 7. Диаграмма графа будет выглядеть так:
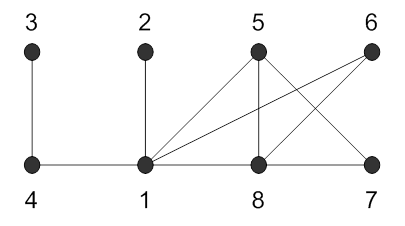
Теперь найдем цикл, не содержащий ребер l7 и l10 .Это будет цикл -15781. Удалим из графа ребро l8, соединяющее вершины 5 и 7.
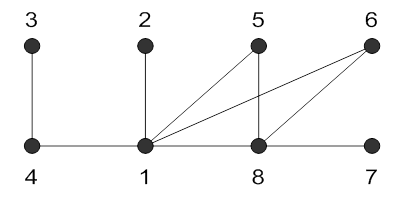
Следующий цикл 1581. Удалим из графа ребро l9, соединяющее вершины 5 и 8.
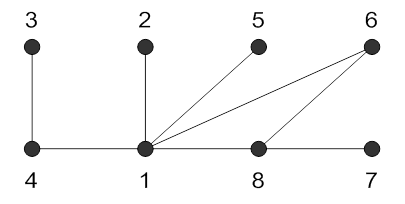
Остался цикл 1681. Удалим из графа ребро l11. В полученном графе циклов нет, и он служит решением данной задачи.
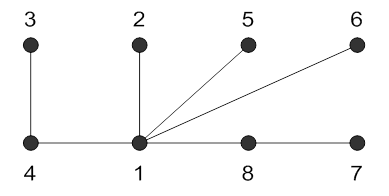
Замечание 1. Для данного графа остов может находиться не единственным способом. Например, для графа из данной задачи остовом может также служить следующий граф:
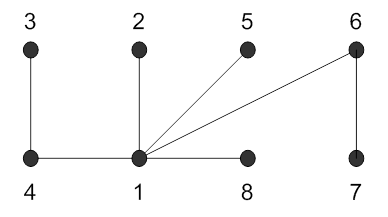
Заметим лишь, что количество ребер в остове графа на 1 меньше количества вершин.
Замечание 2. При решении данной задачи необходимо просматривать также циклы, не выходящие из вершины 1.
Библиографический список
1. С у д о п л а т о в С. В. Элементы дискретной математики/ С. В. С у д о п л а т о в, Е. В. О в ч и н н и к о в а. М.:ИНФРА-М, 2002.
2. К у з н е ц о в О. П. Дискретная математика для инженеров/ О. П. К у з н е ц о в. Краснодар: Лань, 2004.
3. Н о в и к о в Ф. А. Дискретная математика для программистов/ Ф. А. Н о в и –
к о в. СПб: Питер, 2004.
4. Г о н ч а р о в а Г. А. Элементы дискретной математики/ Г. А. Г о н ч а р о в а, А.А. М о ч а л и н. М.:ИНФРА-М, 2004.
5. Ш а п о р е в С. Д. Дискретная математика. Курс лекций и практических занятий/ С. Д. Ш а п о р е в. СПб:БХВ-Петербург, 2006.
6. П л о т н и к о в А. Д. Дискретная математика/ А. Д. П л о т н и к о в. М.: Новое знание, 2006.
7. Ш е в е л е в Ю. П. Дискретная математика/ Ю. П. Ш е в е л е в. СПб: Лань, 2008.
8. Г а т е л ю к О. В. Основы дискретной математики ч1 и 2 / О. В. Г а т е л ю к, В. Г. Ш а н т ар е н к о. Омский ун-т путей сообщения. Омск, 2005.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.