Решения тестовых задач дисциплины "Линейная алгебра и геометрия", страница 2

Если то прямая (13) параллельна плоскости (14), а точка , через которую прямая проходит, лежат вне этой плоскости. Следовательно, прямая (13) в этом случае не имеет с плоскостью (14) ни одной общей точки. Если и , то в силу первого равенства прямая параллельна плоскости (14), а в силу второго равенства точка прямой лежит в этой плоскости. Следовательно, в этом случае вся прямая лежит в этой плоскости.

№6      Привести квадратичную форму к каноническому виду методом ортогональных преобразований.

Метод собственных векторов. Для  того чтобы привести квадратичную форму к каноническому виду, необходимо выписать матрицу квадратичной формы

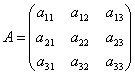
у которой , т.е. элементы, симметричные относительно главной диагонали, совпадают. Затем составляем и решаем характеристическое уравнение:

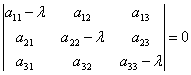
Так как матрица симметричная, то корни характеристического уравнения являются  действительные числа. Найденные собственные числа являются коэффициентами в каноническом виде квадратичной формы в базисе .

Пусть найденные нормированные собственные векторы, соответствующие характеристическим числам в ортонормированном базисе .

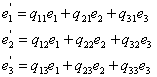
В свою очередь, векторы  образуют ортонормированный базис. Матрица

Является матрицей перехода от базиса к базису .

Формулы преобразования координат при переходе к новому ортонормированному базису имеют вид

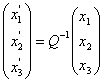
Принято говорить, что квадратичная форма приведена к каноническому виду с помощью ортогонального преобразования B.

Математический анализ

№1      Система отрезков  - система вложенных отрезков, если .

            Теорема о вложенных отрезках: Всякая система вложенных отрезков, длина которых стремится к 0, имеет единственное число принадлежащее всем этим отрезкам.

№2     

№3      Пусть функция y=f(x) дифференцируема в точке х, тогда дифференциалом функции называется главная часть приращения этой функции.

            Если А=0, то dy=0. Можно доказать, что А=f’(x), поэтому df(x)=f’(x).

            Пусть теперь функция y=f(x), тогда , ,

- дифференциал переменной .

            Дифференциал функции, есть приращение ординаты касательной, проведенной к графику функции f(x) при переходе от точки x к точке .