Передаточные функции системы автоматического управления. Типовые воздействия в автоматике переходная характеристика звена. Импульсное входное воздействие, страница 8

 (6), при –∞ < ω < +∞.

Второй случай:

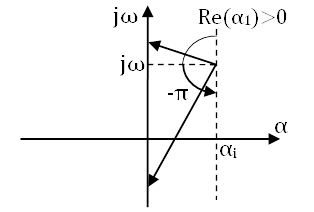То есть λ_i лежит в правой полуплоскости. При изменении частоты –∞ до +∞ конец вектора jω-λ_i скользит вдоль мнимой оси сверху-вниз на угол – π. Тогда изменение аргумента:

 (7).

Предположим, что характеристическое уравнение 1 имеет m корней в правой полуплоскости и l корней в левой полуплоскости, тогда m+l = h (8). h – степень характеристического уравнения. С учетом (8) перепишем выражение для аргумента ΔargD(jω) = π(l-m) = ΔargD(jω) = π(h-2m) (9) Выражение 9 показывает изменение аргумента при изменении частоты от -∞ до +∞ как разность между числом корней характеристического уравнения, лежащих в левой полуплоскости и числом корней, лежащих в правой полуплоскости, умноженное на π.

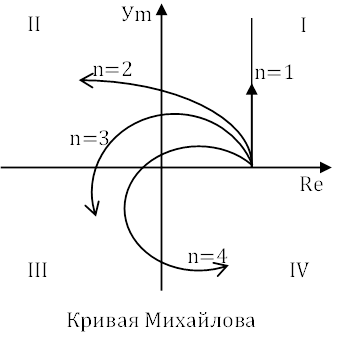
Критерий устойчивости по Михайлову.

Этот критерий устойчивости является геометрической интерпретацией принципа аргумента. Пусть дано характеристическое уравнение D(p) = a_npⁿ+ a_n-1p^n-1+…+ a₀ = 0 (1) для того чтобы системы была устойчивой, необходимо чтобы все корни характеристического уравнения лежали в левой полуплоскости, то есть m=0, тогда ΔargD(jω) = πl (2) при -∞ < ω < +∞.

Геометрическое место точек конца вектора D(jω) при изменении частоты от -∞ до +∞, называется годографом вектора D(jω) или годографом Михайлова.

Произведем замену p на jω, тогда D(jω) = a_n(jω)ⁿ + a_n-1(jω)^n-1 + …+ a₀ = U(ω) – jV(ω). (3)

U(ω) – действительная часть, V(ω) – мнимая часть.

Из математики известно, что действительная часть является четной функцией, а мнимая нечетной:

U(-ω) = U(ω)

V(-ω) = -V(ω)

следовательно D(-jω) = U(ω) – jV(ω) (5)

Из (5) следует что D(-jω) является комплексными сопряженными величинами, то есть можно записать ΔargD(jω)_{при -∞ < ω < 0} = ΔargD(jω)_{при 0 < ω < ∞}  (6)

ΔargD(jω) _{при 0 < ω < ∞} = l (7). Из (7) следует критерий устойчивости по Михайлову:

система будет устойчивой, если при изменении частоты от 0 до +∞ вектор D(jω), начав движение из точки, лежащей на положительной вещественной полуоси комплексной плоскости, вращаясь против часовой стрелки и нигде не обращаясь в 0 обходит последовательно n квадрантов комплексной плоскости, где n - степень характеристического уравнения.

Годограф D(jω) строится по уравнению D(jω), задавая значениями jω и вычисляя действительную и мнимую части. Годограф замкнутой системы можно построить исходя из уравнения передаточной функции замкнутой системы.

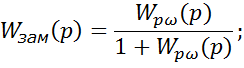
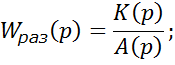
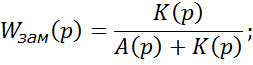
   заменим p на jω:

Затем строим годографы K(jω) и A(jω), и складываем векторы для каждого значения частоты. В случае, если K(jω) = К, то годограф D(jω) получается простым смещением годографа А(jω) вправо, вдоль вещественной оси на величину К, следовательно, построив кривую Михайлова, можно определить критическое значение коэффициента усиления, при котором система будет находиться на границе устойчивости, что соответствует прохождению кривой через начало координат.

Критерий устойчивости Найквиста.

Критерий устойчивости по Найквисту дает возможность судить об устойчивости замкнутой системы, исследуя разомкнутую, что упрощает расчеты. Этот критерий позволяет судить об устойчивости замкнутой системы по экспериментально снятой характеристике разомкнутой системы.

Пусть дана передаточная функция разомкнутой системы: .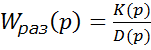

Преобразуем её в функцию 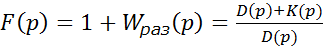 (1).

Числитель - это характеристический полином замкнутой системы, знаменатель – характеристический полином разомкнутой системы. Степени характеристических полиномов имеют следующее значение D(p) = n, K(p) = r (r<n).  (2)

Из (2) можно утверждать, что степень характеристического полинома D(p)+K(p) = n так же равна n. Построим два случая состояния разомкнутой системы.

Случай 1: система в разомкнутом состоянии устойчива, тогда согласно критерию Михайлова можно записать ∆argD(jω)_{при 0<ω<∞}  = n. Для устойчивости системы в замкнутом состоянии должно выполняться условие ∆argD(jω)_{при 0<ω<∞} + K(jω) = n (2).

∆argF(jω) = ∆arg (D(jω)+K(jω))_{при 0<ω<∞} - ∆argD(jω)_{при 0<ω<∞} = 0 (4).