де ![]() . Тут маємо три ряди і міркуємо, як і в
попередньому випадку.
. Тут маємо три ряди і міркуємо, як і в
попередньому випадку.
Ряд з тензорними членами – це ряд ![]() ,
,
де
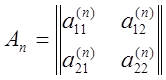 .
.
Тут маємо чотири ряди ![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Міркуємо як вище.
1.7. Наближене обчислення суми ряду. Прискорення збіжності ряду
Обчислення суми ряду виконують після того, як встановлено збіжність
ряду. Знаходять суму за допомогою заміни ![]() на
на ![]() . При цьому допускається похибка
. При цьому допускається похибка
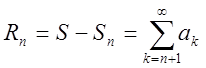 .
.
Оскільки величина допустимої похибки ![]() обумовлена
заздалегідь, то число членів
обумовлена
заздалегідь, то число членів ![]() для підрахунку можна
знайти з нерівності
для підрахунку можна
знайти з нерівності ![]() .
.
При великому ![]() (або при малому
(або при малому ![]() )
порядок
)
порядок ![]() можна оцінити за допомогою виразу
можна оцінити за допомогою виразу
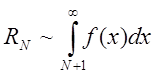 ,
, ![]() ,
,
тобто формула для знаходження необхідного числа членів ряду при
обчислені його суми має вигляд 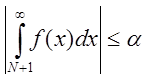 .
.
Звідси знаходимо ![]() , а після цього можна
вже говорити про швидкість збіжності: чим більше
, а після цього можна
вже говорити про швидкість збіжності: чим більше ![]() , тим ця
швидкість менша.
, тим ця
швидкість менша.
П.7. Знайти необхідне число членів ![]() , яке забезпечує обчислення з точністю
, яке забезпечує обчислення з точністю ![]() суми ряду
суми ряду 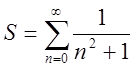 .
.
Розв’язання. Згідно з (13.11), 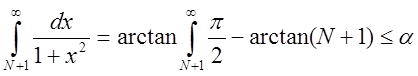 ,
,
Звідки ![]() ,
, ![]() .
.
Якщо інтеграл знайти важко або взагалі неможливо, то замість ![]() можна взяти еквівалентну нескінченно малу,
завдяки чому обчислення інтеграла істотно спрощується, а результат не
змінюється.
можна взяти еквівалентну нескінченно малу,
завдяки чому обчислення інтеграла істотно спрощується, а результат не
змінюється.
П. 8. Розв’язати П. 1, спростивши спочатку підінтегральну функцію.
Розв’язання. Маємо 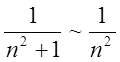 при
при ![]() . Ураховуючи (2.12), дістаємо
. Ураховуючи (2.12), дістаємо
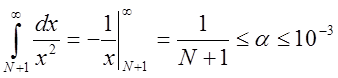 ,
, ![]() ,
,
тобто той же результат, що й у п. 1.
П. 9. Знайти таке ![]() , що
забезпечує обчислення з точністю
, що
забезпечує обчислення з точністю ![]() суми ряду
суми ряду
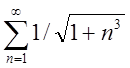 .
.
Розв’язання. Оскільки 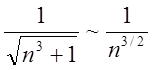 , то з
урахуванням (1.12) маємо
, то з
урахуванням (1.12) маємо
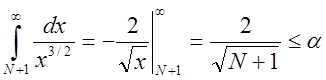 ,
, ![]() .
.
Як бачимо, ряд сходиться повільно, обчислення його суми пов’язане із значними труднощами, особливо при ручному розрахунку, який застосовують навіть не зважаючи на наявність персональних ЕОМ (при різних оцінках, прикидках тощо, необхідних, наприклад, при формуванні математичної моделі).
Ідея прискорення збіжності ряду належить О. М. Кирилову. Вона полягає в
тому, що для даного ряду ![]() підбирають ряд з
відомою сумою
підбирають ряд з
відомою сумою ![]() такий, що
такий, що ![]() при
при ![]() .
Виходячи з властивостей еквівалентних нескінченно малих, маємо
.
Виходячи з властивостей еквівалентних нескінченно малих, маємо ![]() , де
, де ![]() . Тоді
. Тоді
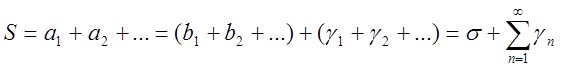 , де останній ряд збігається швидше.
, де останній ряд збігається швидше.
За допоміжний ряд з відомою сумою беруть дзета-функцію Рімана (див.
Узагальнений гармонічний ряд) 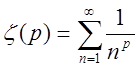 ,
,
яка затабульована. Для довідки: 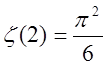 ,
, 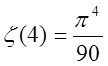 ,
, 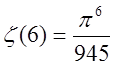 ,
, 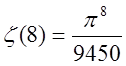 .
.
П.10. Прискорити при ![]() збіжність
ряду
збіжність
ряду 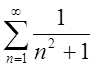 .
.
Розв’язяння. Оскільки 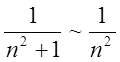 , то
допоміжним рядом є
, то
допоміжним рядом є  .
.
Маємо 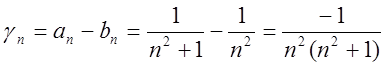 , тобто
, тобто 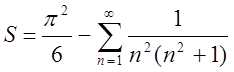 .
.
Оцінимо швидкість збіжності нового ряду:
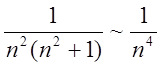 ,
, 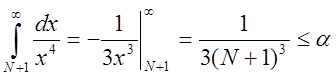 .
.
Отже ![]() . Тоді
. Тоді 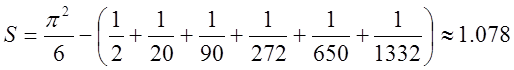 .
.
Наведений метод можна, звичайно, застосувати повторно.
1.8. Запитання для самоперевірки.
Розв´язати самостійно.
1.Дослідити збіжність рядів, використовуючи необхідну ознаку збіжності
1.1. 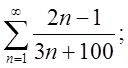 1.2.
1.2. 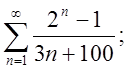 1.3.
1.3. 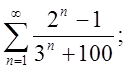 1.4.
1.4. 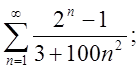 Відп.
Усі розбігаються
Відп.
Усі розбігаються
2.Дослідити збіжність рядів, використовуючи ознаку Даламбера.
2.1. 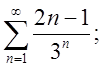 2.2.
2.2. 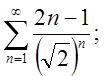 2.3.
2.3.
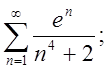 3.4.
3.4.  Відп.1,2
– збіг.3,4 – розбіг.
Відп.1,2
– збіг.3,4 – розбіг.
3.Дослідити збіжність рядів, використовуючи радикальну ознаку Коші.
3.1.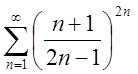 3.2.
3.2. 3.3.
3.3.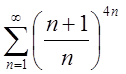 3.4.
3.4.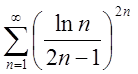 Від.1,2
– збіг.3,4 – розбіг
Від.1,2
– збіг.3,4 – розбіг
4.Дослідити збіжність рядів, використовуючи інтегральну ознаку Коші.
4.1. 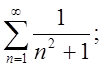 4.2.
4.2. 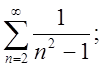 4.3.
4.3. 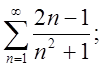 4.4.
4.4. 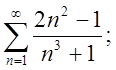 Відп.1,2
– збіг.3,4 – розбіг.
Відп.1,2
– збіг.3,4 – розбіг.
5.Дослідити збіжність знакозмінних рядів, використовуючи ознаку Лейбніца.
5.1. 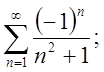 5.2.
5.2. 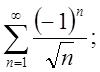 5.3.
5.3. 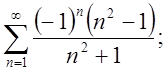 5.4.
5.4. 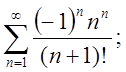
Відп.1-збіг. абсолютно, 2 – збіг. умовно, 3 і 4 – розбігаються.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.