Теорія поля. Скалярне поле. Поверхні рівня. Градієнт. Векторне поле і векторні лінії. Потік вектора через поверхню, страница 3

З виду цієї прямої і випливає, що градієнт     функції  у точці  є напрямним вектором нормалі, що і  потрібно було довести.

Використовуючи те, що градієнт перпендикулярний до поверхні рівня і те, що він є напрямним вектором нормалі до поверхні в даній точці, ми можемо через градієнт виразити одиничний вектор (раніше ми його називали ортом) нормалі до поверхні  в заданій точці: .

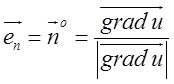Таким чином, градієнт у кожній точці перпендикулярний до дотичної площини, яка проведена до   поверхні рівня, що проходить через дану точку, тобто його проекція на цю площину дорівнює нулю. Отже:

Похідна по будь-якому напрямку, дотичному до поверхні рівня, що проходить через дану точку, дорівнює нулю.

Властивості градієнта функції аналогічні правилам знаходження похідних і доведення двох наступних властивостей очевидне.

1).

2), де С – постійна величина.

Третю і четверту властивість доводимо за правилами диференціювання.

3)

 

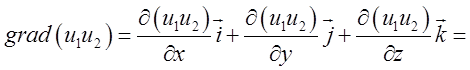
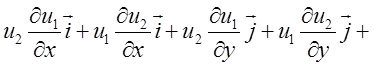
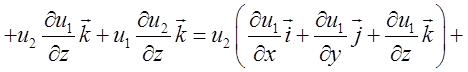
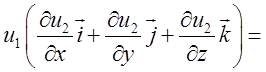
= . Таким чином: .

4) =

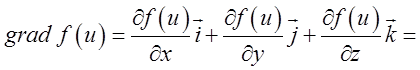
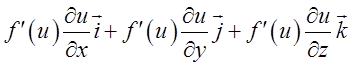=. Таким чином. .

П.1. Знайти поверхні рівня скалярного поля  .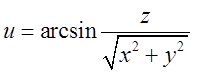

Розв’язок. Знайдемо спочатку область визначення функції:

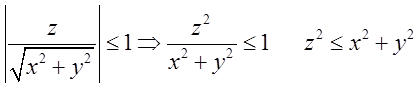; як відомо  є рівняння конуса. Значить нерівність  задає простір який знаходиться зовні конуса. Для цього достатньо взяти яку завгодно точку, про яку ми знаємо, що вона знаходиться зовні, наприклад  і переконатись, що її координати задовольняють нерівність . Поверхні рівня визначаються рівнянням 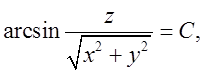 де 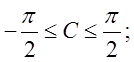Або після очевидних перетворень 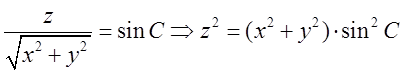. Але ж  тому  - це буде сімейство кругових конусів розташованих зовні конуса  зі спільною віссю симетрії . Сам конус  також входить в це сімейство, а точка - вершина всіх конусів є точкою невизначеності поля.

П.2. Знайти похідну скалярного поля  в точці параболи за      напрямком цієї параболи.

Розв’язок. Знайдемо направляючі конуси вказаного напрямку. Напрям параболи,  в будь-якій точці збігається з напрямком дотичної до параболи в цій точці, а тому знайдемо вектор напрямку (добре було б, коли б він був одиничним) дотичної, використовуючи  геометричний зміст похідної: тангенс кута нахилу до осі  дотичної до кривої в даній точці дорівнює величині похідної в цій точці. Із рівняння 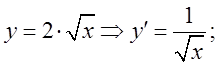 Тому 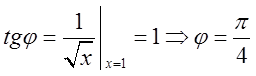; Звідси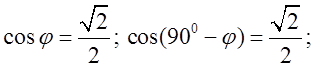  

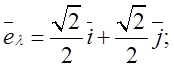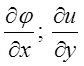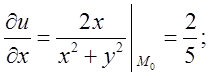
Таким чином   Знайдемо  в точці    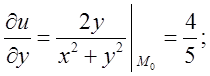      Підставимо знайдені значення в формулу (11.1).

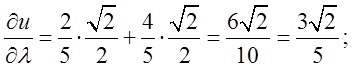 Це і є відповідь.

П.3. Обчислити , де 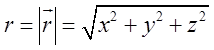 – довжина радіус-вектра  точки , або віддаль цієї точки від початку координат.

Розв. 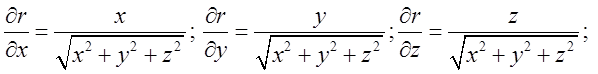Очевидно, що  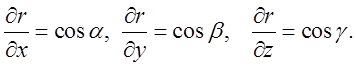А тому .

П.4. Знайти точки, в яких модуль градієнта скалярного поля  дорівнює 1.

Розв’язок:

                                 (*)          

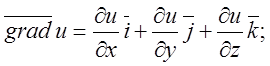
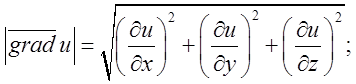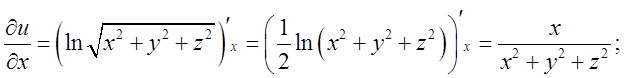
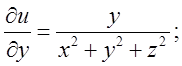
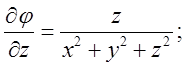        Підставимо в (*)  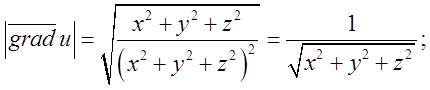    Згідно умови , тобто , а це рівняння сфери.

Відповідь: точки розміщені на сфері .

11.3. Векторне поле і векторні лінії

З векторним полем ми зтикалися в шкільному курсі фізики. З ним ми  працювали, вивчаючи векторну алгебру. І, накінеці, вводячи криволінійний інтеграл, як роботу силового поля по переміщенню матеріальної точки вздовж заданої кривої ми під силовим полем розуміли векторне поле. Силові поля, гравітаційні, магнітні, електричні, поле випромінювання (теплове, радіаційне), поле швидкостей руху та ін. характеризуються одними і тими ж математичними законами. Поле є найбільш загальна сутність існування матерії і найбільш загадкова і незвідана її таємниця.   

Означення. Якщо в кожній точці Р області D задано визначений вектор, то будемо говорити, що в цій області задане векторне поле.

Таким чином ми вважатимемо векторне поле задане, якщо в кожній точці Р поля визначений відповідний цій точці вектор . Ми будемо  розглядати стаціонарні поля, у яких вектор   залежить тільки від точки Р и не залежить від часу. Проекції вектора  на осі координат позначимо через . Якщо точка Р має координати х, у и z, то і сам вектор , і його проекції будуть функціями цих координат, і ми можемо записати:

Далі усюди передбачається, що функції  неперервні разом зі своїми частинними, похідними першого і другого порядків.

Розглянемо деякі окремі випадки векторних полів.

1. О д н о р і д н е    п о л е. Векторне поле називається однорідним, якщо  — постійний вектор, тобто  — постійні величини.

Прикладом однорідного поля може служити, наприклад, поле ваги (Земного тяжіння), поле швидкостей тіла, яке рухається прямолінійно і рівномірно.

2. П л о с к і   п о л я. Якщо в обраній системі координат проекції вектора не залежать від однієї з трьох змінних х,у,z і одна з проекцій дорівнює нулю, наприклад: