ε =![]() .
(2.2.2)
.
(2.2.2)
Подставив ε в выражение (2.2.1), находим функцию распределения электронов по скоростям.
Максимальную скорость
находим, подставив в выражение (2.2.2) энергию Ферми, которую в свою очередь
определяем, проинтегрировав выражение (2.2.1) по всем значениям энергии от 0 до
![]() . Среднюю энергию свободных
электронов находим следующим образом
. Среднюю энергию свободных
электронов находим следующим образом
<ε> =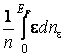 .
.
Вероятность обнаружить электрон с энергией ε при температуре Т равна
![]() .
.
РЕШЕНИЕ. Найдём энергию Ферми. При Т = 0 К число квантовых состояний dz (фазовых ячеек) для свободных электронов с энергиями в интервале (ε, ε+dε) равно
![]() ,
(2.2.3)
,
(2.2.3)
где р – импульс электрона.
Кинетическая энергия ![]() , тогда
, тогда ![]() , и
, и ![]() .
.
Подставив р2
и ![]() в выражение (2.2.3), получаем:
в выражение (2.2.3), получаем:
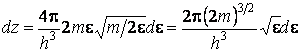 .
.
Введём обозначение ![]() , тогда
, тогда
![]() .
(2.2.4)
.
(2.2.4)
Число свободных
электронов ![]() в интервале энергий (ε, ε+dε) равно произведению числа
в интервале энергий (ε, ε+dε) равно произведению числа ![]() фазовых ячеек на функцию
распределения (2.2.1):
фазовых ячеек на функцию
распределения (2.2.1):
![]()
![]() .
(2.2.5)
.
(2.2.5)
Множитель 2 появился в связи с тем, что в каждой фазовой ячейке (квантовом состоянии) могут находиться два электрона с противоположно направленными спинами. При Т = 0 электроны полностью заполняют все фазовые состояния, и f= 1, тогда
![]() .
(2.2.6)
.
(2.2.6)
Концентрация свободных
электронов n определяется при интегрировании
этого выражения в пределе от ![]() до
до ![]()
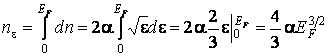 , (2.2.7)
, (2.2.7)
тогда энергию Ферми при Т = 0 можно представить в виде:
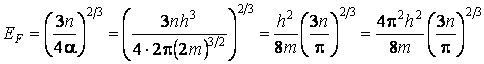 .
(2.2.8)
.
(2.2.8)
Максимальная скорость
электронов соответственно энергии Ферми, 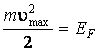 ,
поэтому
,
поэтому 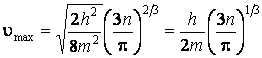 .
.
Проверим размерность: ![]() . Подставим значения:
. Подставим значения:
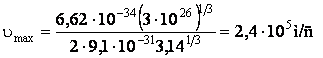 .
.
Чтобы найти функцию
распределения электронов по скоростям при Т = 0, подставим в выражение (2.2.5)
![]() и
и ![]() :
:
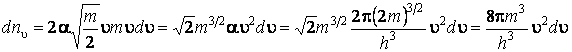 .
.
Проверим размерность 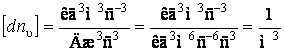 .
.
При Т = 0 К средняя энергия свободных электронов равна интегралу:
<ε>=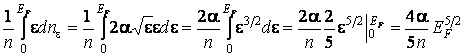 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.