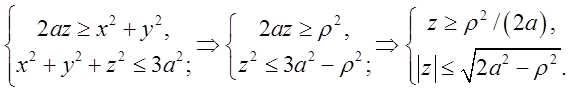 Таким чином:
Таким чином: 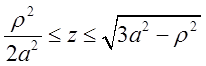 .
.
Перетворимо підінтегральний вираз ![]() =
=
=![]() . Інтеграл буде мати
вид
. Інтеграл буде мати
вид
![]()
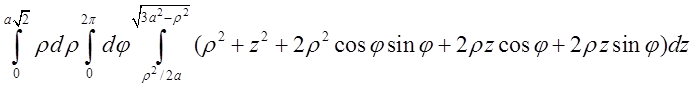 Для
компактності записів внутрішній інтеграл будемо позначати
Для
компактності записів внутрішній інтеграл будемо позначати ![]() , середній
, середній ![]() ,
зовнішній
,
зовнішній ![]() .
.
Обчислимо![]() .
.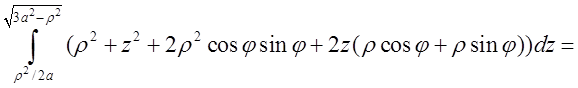
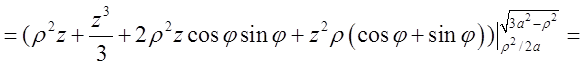
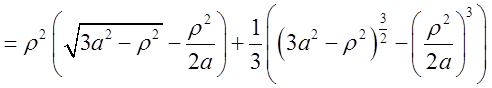 +
+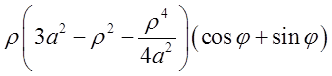 +
+
+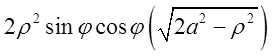 . Поглядаючи на
одержане значення
. Поглядаючи на
одержане значення ![]() і навіть зважаючи на те, що
інтегруючи (середній інтеграл по довжині періоду) суму
і навіть зважаючи на те, що
інтегруючи (середній інтеграл по довжині періоду) суму![]() ,
а також добуток
,
а також добуток ![]() одержимо в обох випадках 0, все
одно зовнішній інтеграл виходить аж занадто громіздким. Тому, незважаючи на те,
що замість одного інтнграла прийдеться обчислювати два, все-таки перейдемо до
сферичної системи координат.
одержимо в обох випадках 0, все
одно зовнішній інтеграл виходить аж занадто громіздким. Тому, незважаючи на те,
що замість одного інтнграла прийдеться обчислювати два, все-таки перейдемо до
сферичної системи координат.
![]() Перетворимо границі
Перетворимо границі
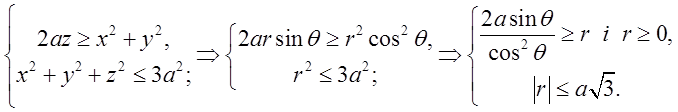
Таким чином границі для r коли змінюється ![]() від 0 до кола BCD, на якому
від 0 до кола BCD, на якому 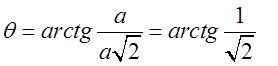 , або
, або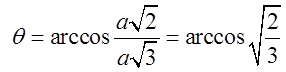 будуть
будуть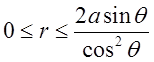 .
.
А якщо ![]() буде
змінюватись від кола BCD до вісі OZ, то границі для r будуть
буде
змінюватись від кола BCD до вісі OZ, то границі для r будуть![]() . Перетворимо підінтегральний
вираз
. Перетворимо підінтегральний
вираз ![]() = =
= =![]() = =
= =![]() . Інтеграл буде розбитим на два інтеграли
(по двох областях). Область
. Інтеграл буде розбитим на два інтеграли
(по двох областях). Область ![]() обмежена конусом і
параболоїдом , Область
обмежена конусом і
параболоїдом , Область ![]() обмежена конусом і сферою.
обмежена конусом і сферою.
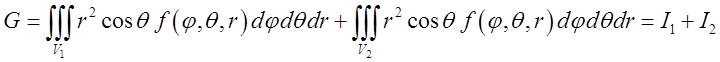 . Обчислимо
. Обчислимо ![]() .
.
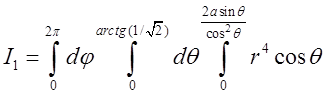
![]() =
=
=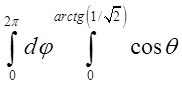
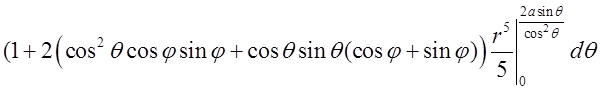 =
=
=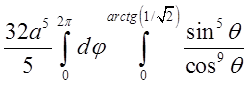
![]() .
.
Знайдемо первісну ![]() від
підінтегральної функції
від
підінтегральної функції
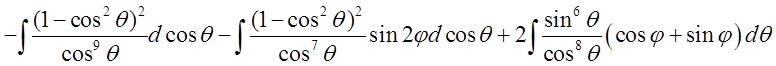 =
=
=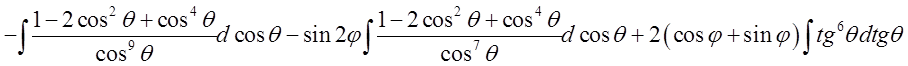 =
=
=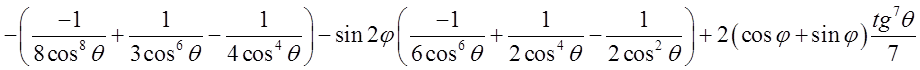 .
.
При ![]() ця первісна дорівнює:
ця первісна дорівнює:
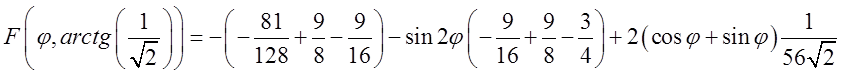 =
=
=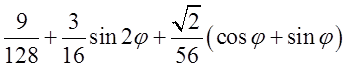 . При
. При ![]() ця первісна дорівнює
ця первісна дорівнює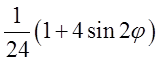 .
.
Так як визначений інтеграл є приріст
первісної, то 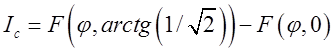
![]()
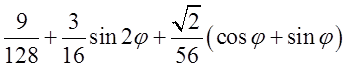 –
–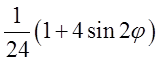 , а зовнішній інтеграл
, а зовнішній інтеграл
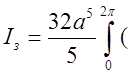
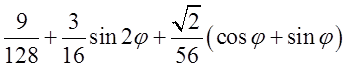 –
–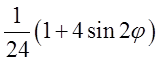
![]() , зважаючи на те, що
інтегруючи по довжині періоду суму
, зважаючи на те, що
інтегруючи по довжині періоду суму ![]() , а також добуток
, а також добуток ![]() одержимо в обох випадках 0, матимемо:
одержимо в обох випадках 0, матимемо: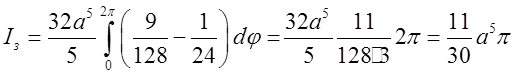 .
.
Обчислимо ![]() .
.
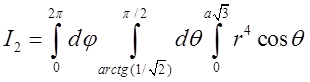
![]() =
=
=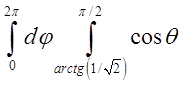
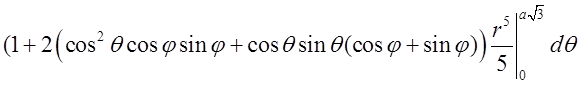 =
=
=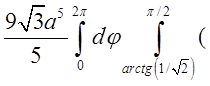
![]() .
.
Знайдемо первісну ![]() від
підінтегральної функції.
від
підінтегральної функції.
![]() =
=![]()
![]() =
=
![]()
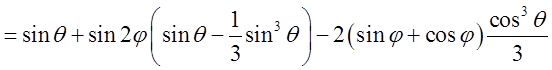 . При
. При ![]() ця первісна дорівнює:
ця первісна дорівнює:
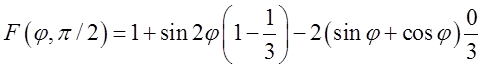 =
=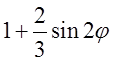 .
.
При ![]() ця первісна дорівнює:
ця первісна дорівнює:
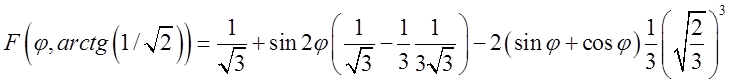 =
=
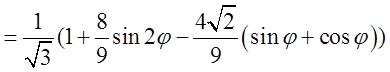 . Таким чином
. Таким чином 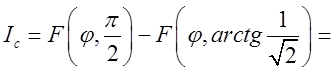
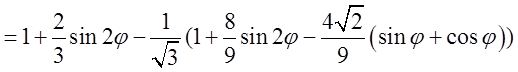 . Зважаючи на те, що
інтегруючи по довжині періоду суму
. Зважаючи на те, що
інтегруючи по довжині періоду суму ![]() , а також добуток
, а також добуток ![]() одержуватимемо в обох випадках 0,
матимемо:
одержуватимемо в обох випадках 0,
матимемо: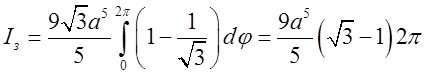 . Загальна відповідь буде
. Загальна відповідь буде
5.4. Узагальнення поняття інтеграла
Розглядаючи задачі, які приводять до поняття того чи іншого
інтеграла (визначеного, подвійного, потрійного), можна побачити, що деякі з них
повторюються, але на різних фігурах, наприклад, задачі знаходження маси,
електричного заряду. При цьому для однієї і тієї ж величини діставали різні
інтеграли. Якщо якась величина (маса, заряд) визначена на відрізку, то маємо
визначений інтеграл, якщо на пластинці, — то подвійний, на просторовому тілі, —
потрійний. Однак та сама маса й електричний заряд можуть бути заданими і на
інших фігурах. Кожній з геометричних фігур поставимо у відповідність її числову
адитивну характеристику, яку називають її мірою. Для відрізка це довжина, для
пластинки — площа, для тіла — об'єм і т.д. Нехай на деякій скінченній
геометричній фігурі А задано певну функцію ![]() (функцію
точки, наприклад, густину речовини).
(функцію
точки, наприклад, густину речовини).
Розіб'ємо фігуру на п частин довільним способом. ![]() — це і множина точок і-ї
частини А, і її міра. Вважатимемо, що
— це і множина точок і-ї
частини А, і її міра. Вважатимемо, що ![]() .
.
Суму 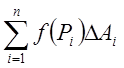 називатимемо
інтеґральною сумою для
називатимемо
інтеґральною сумою для ![]() по А. Інтегралом від
по А. Інтегралом від ![]() по області А називають границю
по області А називають границю
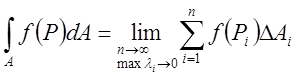 , (5.17)
, (5.17)
де ![]() — диференціал відповідної міри,
— диференціал відповідної міри, ![]() — діаметр
— діаметр ![]() .
Властивості інтеґрала (5.17) аналогічні властивостям одно- двох- і трьохвимірного
інтеграла.
.
Властивості інтеґрала (5.17) аналогічні властивостям одно- двох- і трьохвимірного
інтеграла.
Запитання для самоперевірки.
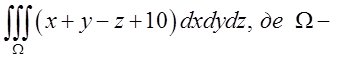 куля
куля ![]() .
.
Розвяжіть самостійно.
1.1.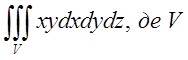 – область, обмежена гіперболічним
параболоїдом
– область, обмежена гіперболічним
параболоїдом ![]() і площинами
і площинами
![]() Відп.
Відп.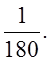
1.2.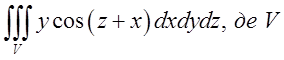 – область, обмежена циліндром
– область, обмежена циліндром ![]() і площинами
і площинами
![]() Відп.
Відп.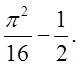
1.3.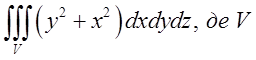 – область задана нерівностями
– область задана нерівностями ![]() .
.
Відп. 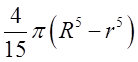 .
.
1.4.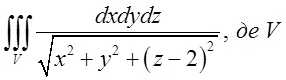 – куля
– куля ![]() .
Відп.
.
Відп. ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.