








Лекція 8
План.
1. Обчислення площ, об'ємів, довжин кривих за допомогою визначених інтегралів.
2. Фізичний додаток.
1. Обчислення площ, об'ємів, довжин кривих за допомогою визначених інтегралів.
З геометричного
змісту визначеного інтеграла випливає, що площа криволінійної трапеції,
розташованої вище осі Ох (![]() ), дорівнює
), дорівнює
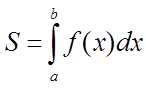 або
або 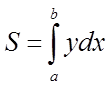 .
.
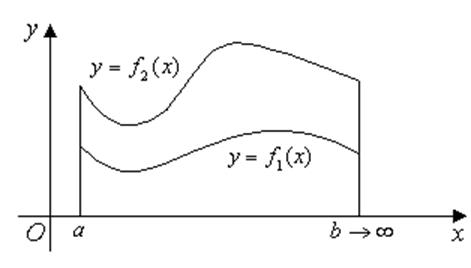
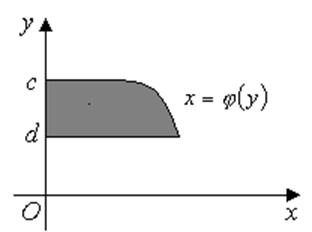
Площу фігури,
обмеженої кривими ![]() і
і ![]() ,
прямими
,
прямими ![]() і
і ![]() (за
умови, що
(за
умови, що ![]() і
і ![]() ),
можна знайти за формулою
),
можна знайти за формулою
 |
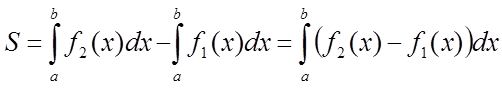 .
.
 |
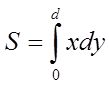 .
.
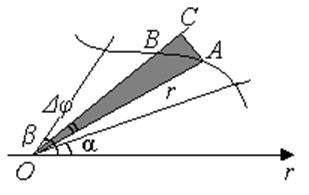
Знайдемо площу S
криволінійного сектора, тобто плоскої фігури, обмеженою безперервною лінією
![]() і двома променями φ=α і φ=β
(α <β), де r і φ – полярні координати.
і двома променями φ=α і φ=β
(α <β), де r і φ – полярні координати.
 Вважаємо частину шуканої площі S
як функцію кута φ, тобто
Вважаємо частину шуканої площі S
як функцію кута φ, тобто ![]() , де
, де ![]() .
.
Якщо кут φ одержить збільшення Δφ=dφ, то збільшення площі ΔS дорівнює площі «елементарного» криволінійного сектора ОАВ.
Диференціал d
являє собою головну частину збільшення ΔS при dφ→0 і дорівнює
площі кругового сектора ОАС радіуса r з центральним кутом dφ.
Тому 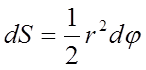 .
.
Інтегруючи отриману рівність у межах від φ=α до φ=β, одержимо шукану площу
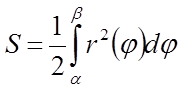 .
.
Наприклад:
обчислити площу фігури, обмеженої лінією ![]() .
.
Знайдемо площу половини фігури, при цьому кут φ буде змінюватися від 0° до 180°.
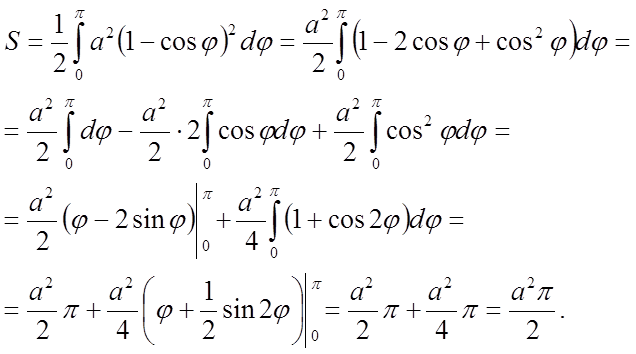
Обчислення довжини дуги плоскої кривої в декартовій системі координат
Під довжиною дуги АВ розуміють межу, до якої прагне довжина ламаної лінії, уписаної в цю дугу, коли число ланок ламаної необмежено зростає, а довжина найбільшої її ланки прагне до нуля.
Якщо функція ![]() і її похідна
і її похідна ![]() безперервні
на відрізку
безперервні
на відрізку ![]() , то крива АВ має довжину, яка
дорівнює
, то крива АВ має довжину, яка
дорівнює
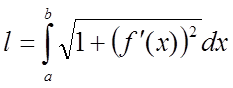 .
.
Розіб'ємо
відрізок ![]() на n рівних частин, проведемо хорди
на n рівних частин, проведемо хорди
![]() , довжини яких позначимо через
, довжини яких позначимо через ![]() , одержимо
, одержимо
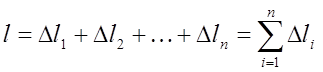 .
.
З ![]() можна знайти довжину хорди за теоремою
Піфагора:
можна знайти довжину хорди за теоремою
Піфагора:
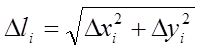 , тому що
, тому що ![]() ,
,
те 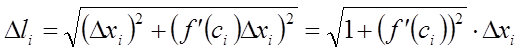 .
.
Довжина всієї
ламаної ![]() дорівнює
дорівнює
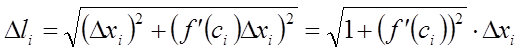 .
.
За визначенням довжина l кривій АВ дорівнює:
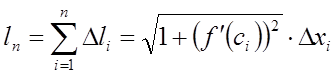
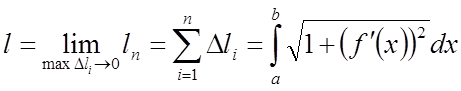 , або
, або
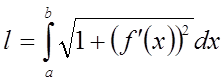 .
.
Якщо рівняння кривій АВ задано в параметричній формі:
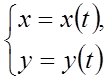 , де
, де ![]() ,
функції
,
функції ![]() ,
, ![]() –
безперервні функції, то довжина дуги знаходиться за формулою:
–
безперервні функції, то довжина дуги знаходиться за формулою:
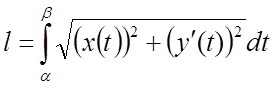 , тому що
, тому що 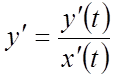 ,
, ![]() .
.
Наприклад: рівняння окружності в параметричному виді записується:
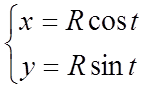 , де
, де ![]() .
.
Обчислимо довжину окружності:
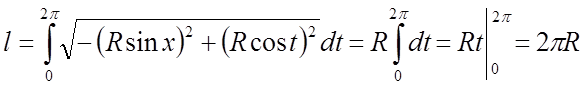 .
.
Нехай крива АВ
задана рівнянням у полярних координатах ![]() ,
, ![]() , тоді
, тоді
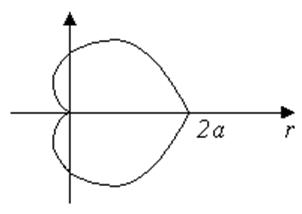
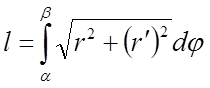 .
.
Наприклад: знайти довжину кардіоїди ![]() ,
, ![]() .
.
Знайдемо половину довжини кардіоїди
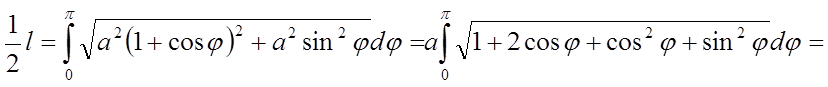
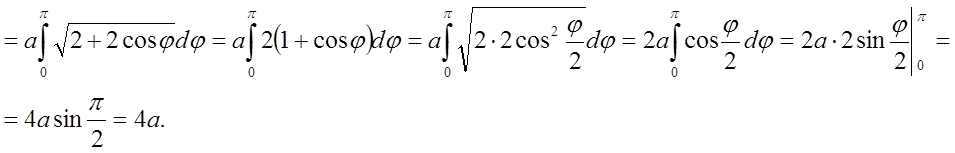 Отже, l=8а.
Отже, l=8а.
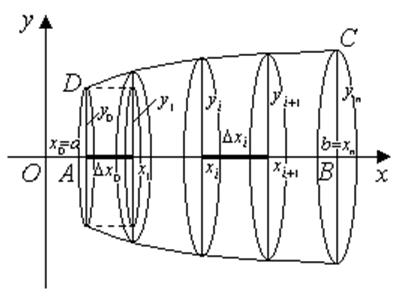 |
Розділимо
відрізок АВ на n малих частин крапками, абсциси яких позначимо
через ![]() . Проведемо з крапок розподілу прямі,
паралельні вісі Оу. Криволінійна трапеція АВС розіб'ється при
цьому n на «тонких» трапецій, довжини основ яких позначимо через
. Проведемо з крапок розподілу прямі,
паралельні вісі Оу. Криволінійна трапеція АВС розіб'ється при
цьому n на «тонких» трапецій, довжини основ яких позначимо через ![]() .
.![]()
Тіло, що вийде після обертання трапеції АВС, виявиться розбитим на n частин. Шуканий обсяг V також розіб'ється на n частин.
Замінимо
криволінійну трапецію за номером i прямокутником з довжиною ![]() і висотою
і висотою ![]() . Кожен
такий прямокутник утворить круглий циліндр, обсяг якого дорівнює
. Кожен
такий прямокутник утворить круглий циліндр, обсяг якого дорівнює ![]() .
.
Складемо інтегральну суму
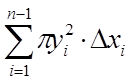 ,
,
яка являє собою наближений вираз шуканого обсягу.
При переході до межі одержимо обсяг тіла
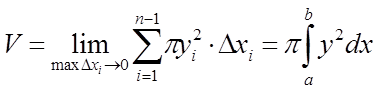 .
.
Отже, 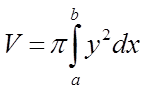 , де
, де ![]() .
.
2. Фізичний додаток.
Нехай на площині ХОY
дано n матеріальних крапок ![]() , маси яких відповідно
рівні
, маси яких відповідно
рівні ![]() .
.
З механіки відомо, що статичні моменти системи цих крапок осей Ох і Оу визначаються формулами
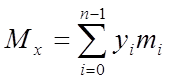 ,
, 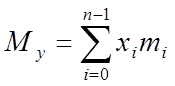 .
.
При 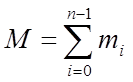 (сума мас) координати центра ваги даної
системи визначаються формулами:
(сума мас) координати центра ваги даної
системи визначаються формулами:
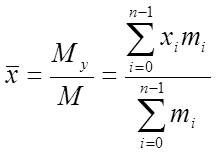 ;
; 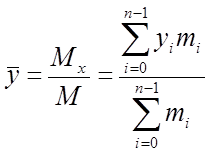 .
.
Нехай потрібно визначити статистичний момент (щодо осей Ох і Оу) і центр ваги дуги, що для простоти вважаємо однорідною щільністю, рівною 1.
Розділимо дугу АВ на n малих частин крапками
![]() .
.
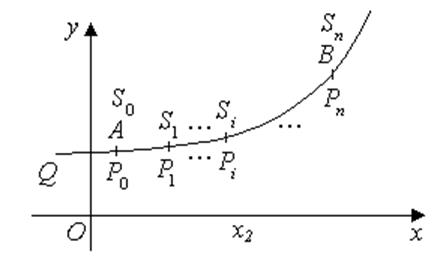 |
Позначимо координати крапок розподілу відповідно:
![]() ,
,
а довжини дуг ![]() позначимо
позначимо
![]() . Припустимо, що маса
. Припустимо, що маса ![]() дуги
дуги ![]() , рівна
, рівна ![]() , зосереджена в деякій крапці
, зосереджена в деякій крапці ![]() цієї дуги.
цієї дуги.
Складемо інтегральні суми:
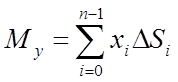 ,
, 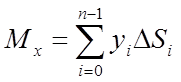 ,
, 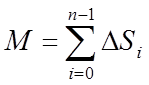 .
.
Перші дві з цих сум є наближеними виразами статичних моментів дуги АВ щодо осей Оу й Ох. Третя сума дає довжину всієї дуги АВ. Тоді наближені вирази координат центра ваги дуги АВ можна записати так:
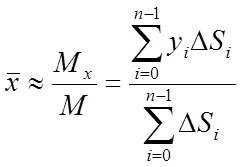 ,
, 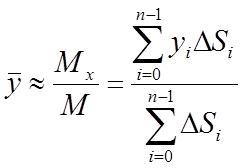 .
.
Перейшовши до межі, одержимо статичні моменти дуги АВ щодо осей Ох і Оу:
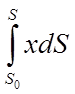 та
та 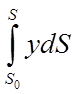 .
.
Довжину дуги АВ
виразимо інтегралом: 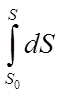 .
.
Тоді координати центра ваги дуги АВ визначається формулами:
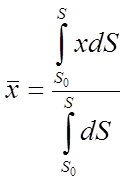 ,
, 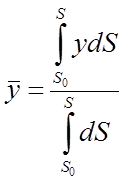 .
.
Нехай на площині ХОY дано n матеріальних крапок
![]() ,
,
маси яких відповідно рівні ![]() . З механіки відомо, що моменти інерції
такої системи щодо осей Ох і Оу і початку координат визначаються
формулами:
. З механіки відомо, що моменти інерції
такої системи щодо осей Ох і Оу і початку координат визначаються
формулами:
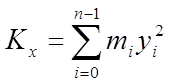 ,
, 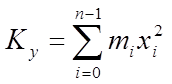 ,
, 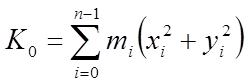 .
.
Нехай тепер
замість системи кінцевого числа матеріальних крапок маємо дугу АВ кривої
![]() .
.
Проводячи аналогічні міркування, одержимо наступні формули для її моментів інерції щодо осей Ох і Оу і крапки О:
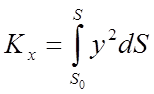 ,
, 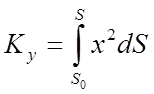 ,
, 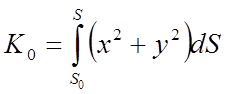 .
.
Механічні додатки визначеного інтеграла
Нехай матеріальна
крапка М переміщується уздовж осі Ох під впливом перемінної сили ![]() , спрямованої паралельно до цієї осі.
Робота, зроблена силоміць при переміщенні крапки М з положення х = а
в положення х = b (а < b), знаходиться за формулою
, спрямованої паралельно до цієї осі.
Робота, зроблена силоміць при переміщенні крапки М з положення х = а
в положення х = b (а < b), знаходиться за формулою
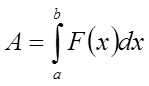 .
.
Тиск рідини на вертикальну пластину
Тиск рідини на
горизонтальну пластину дорівнює вазі цієї рідини, що має основою пластину, а
висотою – глибину її занурення від поверхні рідини, тобто ![]() ,
,
де q – прискорення вільного падіння; γ – щільність пластини;
S – площа пластини; h – глибина її занурення.
За цією формулою не можна шукати тиск рідини на вертикально занурену пластину, тому що її різні крапки лежать на різних глибинах.
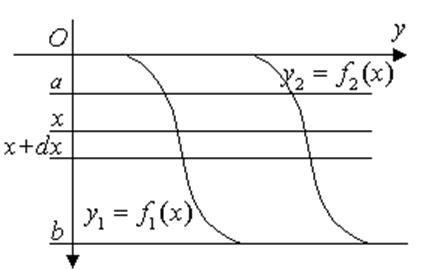 |
Знайдемо тиск Р
рідини на цю пластину, для цього вважаємо частину шуканої величини Р
функцією від х: ![]() , тобто
, тобто ![]() – тиск на частину пластини, що відповідає
відрізкові
– тиск на частину пластини, що відповідає
відрізкові ![]() значень перемінної х, де
значень перемінної х, де ![]() (
(![]() ,
, ![]() ).
).
Дамо аргументові х
збільшення ![]() . Функція
. Функція ![]() одержить
збільшення
одержить
збільшення ![]() . Знайдемо диференціал dp цієї
функції. Через малість dx будемо приблизно вважати смужку прямокутником,
усі крапки якого знаходяться на одній глибині х, тобто пластина ця –
горизонтальна. Тоді за законом Паскаля
. Знайдемо диференціал dp цієї
функції. Через малість dx будемо приблизно вважати смужку прямокутником,
усі крапки якого знаходяться на одній глибині х, тобто пластина ця –
горизонтальна. Тоді за законом Паскаля 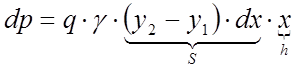 .
.
Інтегруючи отриману рівність у межах від х = а до х = b, одержимо
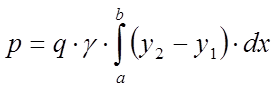 або
або 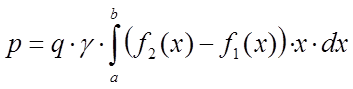 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.