Наблюдаемость в линейных системах управления

Лекция  5

Тема:  Наблюдаемость в линейных системах

управления.

План:

1.  Полная и неполная наблюдаемость в многомерной системе управления.

2.  Критерий наблюдаемости.

3.  Частные случаи критерия наблюдаемости в стационарной системе.

4.  Двойственность понятий управляемости и наблюдаемости для стационарной системы управления.

При функционировании реальных систем управления важным является процесс определения координат вектора состояния системы в определенные моменты времени . Можно произвольно менять состояние замкнутой системы в том случае, если все компоненты вектора состояния доступны для измерения.

На практике, как правило, не все компоненты вектора состояния доступны для измерения (например, потому, что часть переменных состояния в принципе нельзя измерить). Обычно выходными величинами объекта служат лишь отдельные компоненты вектора состояния, либо линейные комбинации этих компонент. В связи с этим в теории управления рассматриваются так называемые задачи о наблюдаемости, основным содержанием которых является установление алгоритмов определения части или всех координат системы при условии, что известна другая часть координат или некоторые функции от этих координат, а также математическая модель системы управления в виде системы дифференциальных уравнений.

Пусть система управления описывается следующими уравнениями:

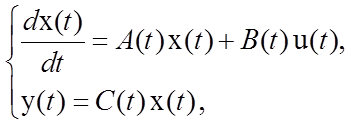                               (5.1)

где , , – непрерывные матрицы порядка , ,  соответственно;  – -вектор выходных (измеряемых) координат системы управления.

Наша цель состоит в том, чтобы для системы (5.1) восстановить вектор состояния  или найти оценку этого вектора  по данным о входной  и выходной  переменным системы. Близость оценки  к истинному вектору состояния  понимается, по крайней мере, в двух смыслах: либо как стремление ошибки оценки к нулю, т.е.  при , либо как точное совпадение вектора состояния  и вектора оценки  в момент после наблюдения выходных переменных объекта в течение конечного отрезка времени  при  или  при .

В нестационарной линейной системе различают следующие две задачи об оценке текущего состояния системы: задача наблюдаемости и задача идентифицируемости системы управления.

Задачей наблюдения называют задачу оценки состояния системы в момент времени  по известным входным и выходным воздействиям, измеренным в будущем, т.е. по данным  и  при .

Задачей идентификации называют задачу определения состояния системы в момент времени  по данным о входных и выходных величинах, измеренных в прошлом, т.е. по данным  и  при .

Часто не делают различия между задачей наблюдения и задачей идентификации, объединяя оба эти понятия термином наблюдаемость. Иногда определяют наблюдаемую систему как систему, в которой по прошлым значениям выходных величин можно судить о состоянии в настоящий момент времени. Этого определения мы и будем придерживаться.

Определение. Задача нахождения вектора  состояния системы (5.1) или отдельных его компонент по известной на некотором промежутке  функции

,                                         (5.2)

где  – известная прямоугольная матрица размерности , называется задачей наблюдаемости линейной системы (5.1). При этом  – функция  выхода системы (5.1).

Определение. Если задача наблюдаемости для системы (5.1) имеет решение, то система называется полностью наблюдаемой или частично наблюдаемой в зависимости от того, все или часть компонент вектора  удается установить.

Определение. Пара матриц ,  называется наблюдаемой, если можно решить задачу о наблюдаемости для системы (5.1) по известному вектору выхода (5.2).

Рассмотрим вначале наиболее простое решение задачи о наблюдаемости однородной системы (5.1) при  и достаточные условия наблюдаемости пары матриц , .

Теорема 4.4. Пусть для каждого значения  существуют и известны  производные от вектора выхода (5.2) системы (5.1). Тогда для существования решения задачи о наблюдаемости системы (5.1) в фиксированной точке  в виде линейной комбинации от значений  и ее производных  достаточно, чтобы

,                                           (5.3)

где

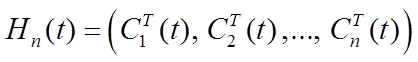,                        (5.4)

,     .

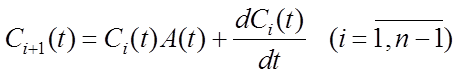Доказательство. Продифференцируем  раз соотношение (5.2), тогда получим  равенств

,

.   .   .   .   .   .   .   .   .   .   .   .   .   .   .   .   .   .   .   .   .   .

,

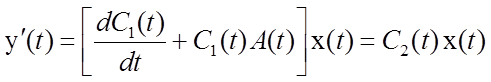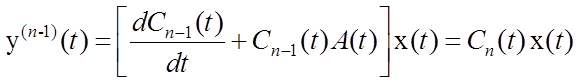рассматриваемых как система линейных алгебраических уравнений относительно компонент вектора . Для существования решения данной системы достаточно, чтобы ранг ее матрицы равнялся .

Но ранг этой матрицы равен рангу сопряженной матрицы, т.е. рангу матрицы , что и требовалось доказать.

Замечание 1. В частном случае, когда вектор выхода является скалярной величиной, т.е. если  – -мерная вектор–функция, соотношение (5.4) примет вид

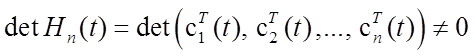,                     (5.5)

где  ,  .

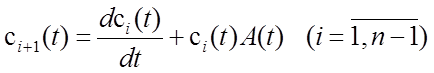Замечание 2. В случае, если система (5.1) стационарна и , то матрица (5.4)  примет вид

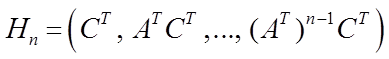
или

,

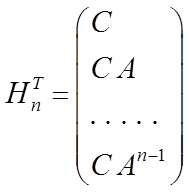а формула (5.5) при :

.

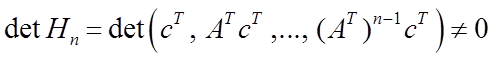При этом фазовые координаты можно определить следующим образом:

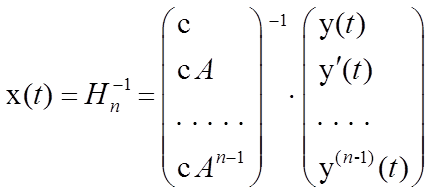
Замечание 3. Решение задачи о наблюдаемости при использовании значений вектора выхода и его производных иногда становится неудобным для практического применения в конкретных системах управления, поскольку при этом требуется вычислять производные от заданной функции, что сопряжено с большими трудностями.

Рассмотрим другой подход к задаче наблюдаемости систем [1].