Методы вариационного исчисления

Лекция  6.

Тема:  Методы вариационного исчисления. 

План:

1.  Постановка задачи оптимального управления как вариационной задачи.

2.  Классификация задач оптимального управления: по виду ограничений, по виду краевых условий, по критерию оптимальности..

3.  Необходимые условия экстремума функционала: уравнения Эйлера.

4.  Достаточные условия экстремума функционала: условия Лежандра.

5.  Задача оптимального управления на условный экстремум.

6.  Каноническая форма уравнений Эйлера-Лагранжа.

Задачей вариационного исчисления является задача отыскания функций, доставляющих экстремальное (максимальное или минимальное) значение определенным величинам, которые зависят от этих функций и называются функционалами. Функционал можно рассматривать как функцию особого рода, в которой роль независимой переменной играет другая функция.

Задача синтеза (построения) оптимального управления формулируется как вариационная задача. При этом кроме уравнений объекта управления должны быть заданы ограничения на управление и фазовые координаты, краевые условия и выбран критерий оптимальности.

Пусть уравнение объекта задается в нормальной форме

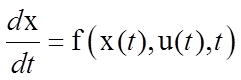                                     (6.1)

или в скалярном виде

,

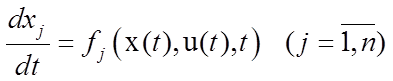где 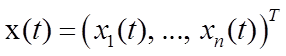 – фазовый вектор;  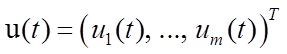– вектор управления. Известно, что любое уравнение, разрешимое относительно старшей производной, можно преобразовать к равносильной нормальной системе уравнений.

На управление и фазовый вектор могут быть наложены ограничения в виде конечных соотношений – равенств, неравенств. Их в общем виде можно записать так:

,    .                                   (6.2)

Здесь  и  – некоторые заданные множества, зависящие, вообще говоря, от времени, причем 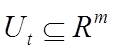 и 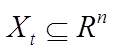. В (6.2) первое соотношение называется ограничением на управление, второе соотношение – ограничением на фазовый вектор или фазовым ограничением. Ограничения на управление и фазовый вектор могут быть не разделены, и в общем случае записаны в виде

.

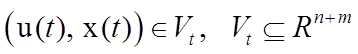Краевые (граничные) условия – ограничения на фазовый вектор в начальный  и конечный  моменты времени в общем виде можно записать так:

.                                 (6.3)

Вектор  называют левым, а вектор  – правым концом траектории. Краевые условия имеют вид (6.3), если ограничения на левый и правый конец траектории разделены. В противном случае они записываются в виде

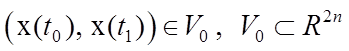
Критерий оптимальности, который является числовым показателем качества системы, задается в виде функционала

.                                            (6.4)

Задача оптимального управления формулируется следующим образом:

Определение. При заданных уравнении объекта управления (6.1), ограничениях (6.2) и краевых условиях (6.3) требуется найти такое управление  и фазовую траекторию 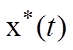, при которых критерий (6.4) принимает минимальное (или максимальное) значение. Тогда управление 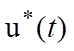 и траектория  называются оптимальными.

В дальнейшем для определенности примем, что функционал (6.4) минимизируется. Задачу максимизации выбором нового критерия  всегда можно свести к задаче минимизации.

В зависимости от вида ограничений (6.2), вида краевых условий (6.3), времени начала и окончания процесса управления, а также критерия оптимальности (6.4) выполняется классификация задач оптимального управления.

1.  По виду ограничений различают задачи:

a)  классического типа, когда ограничения задаются в виде равенства

;                                      (6.5)

b)  неклассического типа, когда ограничения задаются в виде неравенств

.                                    (6.6)

К классическому типу относятся также изопериметрические задачи, т.е. задачи с изопериметрическими ограничениями:

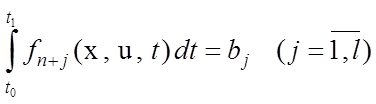.                            (6.7)

Введением дополнительных переменных от изопериметрических ограничений всегда можно избавиться. Достаточно вместо изопериметрических ограничений (6.7) в условие задачи ввести следующие уравнения и краевые условия:

,  ,     

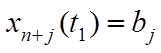
Формально задачи неклассического типа введением дополнительных переменных можно преобразовать к задачам классического типа. Действительно, ограничения (6.6) можно заменить ограничениями типа равенств

.

Задачи оптимального управления неклассического типа могут иметь ограничения вида

.

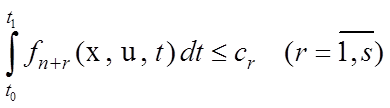Введением дополнительных переменных эти ограничения могут быть заменены соотношениями

,  ,     .

2.  По виду краевых условий различают задачи:

a)  с фиксированными (закрепленными) концами траектории, когда каждое из множеств  и  состоит из одной точки, т.е. , ,  и  – заданные точки;

b)  с подвижным правым концом ( состоит более чем из одной точки), с подвижным левым концом ( состоит более чем из одной точки), с подвижными концами (оба конца подвижны);

c)  со свободным правым концом ( совпадает со всем фазовым пространством, т.е. правый конец траектории без ограничений).

3.  По времени начала и окончания процесса различают задачи:

a)  с фиксированным временем, когда начальный  и конечный  моменты времени фиксированы;

b)  с нефиксированным временем, когда один из моментов времени  или  не фиксирован.

4.  По критерию оптимальности различают:

a)  задачу Больца; при этом критерий имеет вид

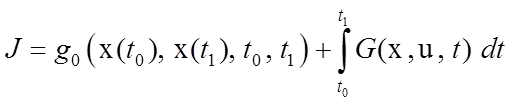
b)  задачу Лагранжа; при этом критерий имеет вид

;

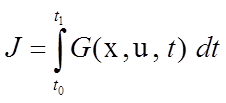c)  задачу Майера; при этом критерий имеет вид

.

Задача Майера в частном случае, когда функционал имеет вид , называется задачей максимального (оптимального) быстродействия.

Задачи Больца, Лагранжа и Майера эквивалентны в том смысле, что путем преобразования переменных можно от одной задачи перейти к другой.