Методи розв'язання лінійних систем диференціальних рівнянь з постійними коефіцієнтами

Розділ 2

МЕТОДИ РОЗВ'ЯЗАННЯ ЛІНІЙНИХ СИСТЕМ ДИФЕРЕНЦІАЛЬНИХ РІВНЯНЬ З ПОСТІЙНИМИ КОЕФІЦІЄНТАМИ

2. 1 Зв'язок теорії матриць із інтегруванням лінійних систем

Розглянемо лінійну однорідну систему

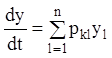(k=1,2,…,n),                                           (2...1)

де Тоді, виходячи із загальної теорії лінійних систем, можна стверджувати, що система (2.1) має фундаментальну систему розв'язань на нескінченному інтервалі :

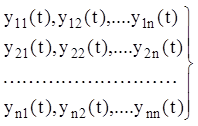                                                    (2.2)

або

         (k = 1,2,…n)                                 (2...3)

Ця система містить функцій. Останні утворюють елементи квадратної матриці n-го порядку

,                                                      (2.4)

яку називають інтегральною матрицею.

У свою чергу, постійних коефіцієнтів правих частин системи рівнянь (2.1),

(k,l =1,2,…,n) утворять елементи постійної матриці n-го порядку

.                                                        (2.5)

Представляє великий теоретичний і практичний інтерес дослідження аналітичної структури елементів інтегральної матриці (8.4) (фундаментальної системи розв'язань) залежно від елементів матриці (2.5), а також способи її побудови по указаній матриці (2.5). Дійсно, з'ясування структури й можливість побудови інтегральної матриці (2.4), як відомо з теорії лінійних систем, забезпечує вивчення властивостей і побудову загального розв'язання однорідної системи виду (2.1), а також і неоднорідної системи більш загального виду

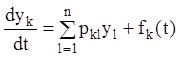        ( k = 1,2,…,n)...                         (2.6)

Нижче буде розглянуте питання побудови інтегральної матриці (2.4) по відомій матриці коефіцієнтів (2.5).

Для цього нам будуть потрібні деякі відомості з теорії матриць.

2.2 Відомості з теорії матриць. Побудова нормальної жорданової форми по відомим елементарним дільникам

Матриця A(t) називається функціональною, якщо її елементи є функції від t, і неперервні на деякому інтервалі, якщо всі її елементи неперервні на цьому інтервалі.

Стовпець (одноколонна матриця)  складається з n величин  (i = 1,2,…,n)

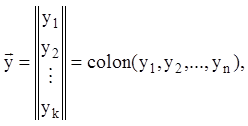
називається n-мірним вектором-стовпцем. Величини називаються координатами вектора . Іноді вживається й вектор-рядок  Добуток матриці A на n-мірний вектор-стовпець тобто є знову n-мірний вектор:

компоненти якого визначаються по формулах:

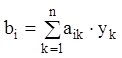
Якщо матриця A є квадратною матрицею порядку n  (k,l=1,2,…,n), то матрицю  або називають характеристичною матрицею, а її визначник  – характеристичним многочленом. Рівняння  називають характеристичним рівнянням, що відповідає матриці A, а його корінь (i = 1,2,…,n) – власними або характеристичними числами матриці A.

Дві матриці A й B одного порядку називають подібними, якщо існує невироджена матриця  порядку n така, що

.

Власні числа подібних матриць  й  збігаються. Дійсно, рівняння

можна записати:

що й доводить наше твердження.

Розглянемо матрицю

,

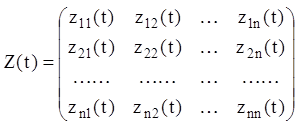елементи якої є функціями від t,  Припустимо, що кожен елемент матриці Z(t) має похідну в точці ,  Тоді похідну від матриці Z(t) у точці визначають так:

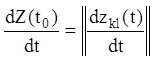                                                        (2.7)

і, таким чином, диференціювання матриці зводиться до диференціювання всіх її елементів. Звичайні правила диференціювання функцій мають місце й для диференціювання матриць.

Якщо  постійна матриця, то:

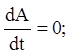
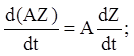
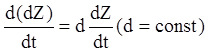                              (2.8)

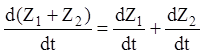                                            (2.9)

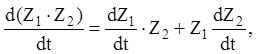                                      (2.10)

причому у формулі (2.9) не можна переставляти співмножники.

Похідна від цілої додатної степені матриці Z(t) обчислюється шляхом послідовного диференціювання:

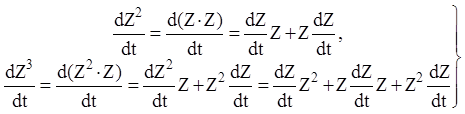                    (2.11)

і т.д.

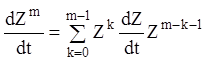.                                               (2.12)

Формула (2.11) спрощується, якщо матриця Z(t) комутирує зі своїй похідній, тобто:

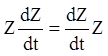                                                         (2.13)

і приймає вид:

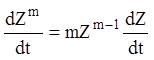.                                                   (2.14)

Операція інтегрування матриці визначається як операція, зворотна диференціюванню:

                                                    (2.15)

або 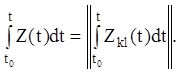                                                                                                          (2.16)

Мають місце властивості (A – постійна матриця):

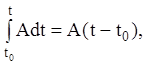
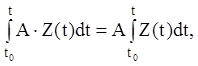                                     (2.17)

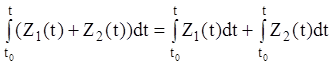                                   (2.18)

Діагональною матрицею називається квадратна матриця n-го порядку, що має всі елементи, що не стоять на головній діагоналі, рівними нулю, і позначається:

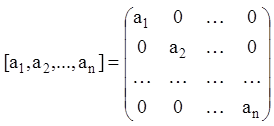                                            (2.19)

Квазідіагональною матрицею структури називається квадратна матриця n-го порядку виду:

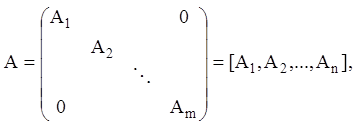                                   (2.20)