![]()
Приклад 2.. Знайти елементарні дільники матриці:
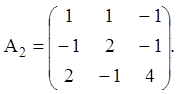
Розв’язання. Будуємо характеристичне рівняння й знаходимо його корінь:
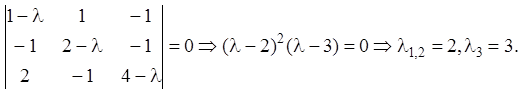
Ранг матриці 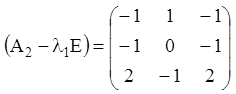 дорівнює
дорівнює ![]() число
елементарних дільників, що відповідають
число
елементарних дільників, що відповідають ![]() дорівнює
дорівнює
![]() Отже, елементарним дільником, що
відповідає
Отже, елементарним дільником, що
відповідає ![]() буде
буде ![]() Тому що
друге характеристичне число простої, то елементарними дільниками матриці A
будуть:
Тому що
друге характеристичне число простої, то елементарними дільниками матриці A
будуть:
![]()
Приклад 1. Дано матрицю 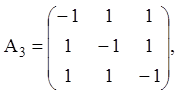 знайти її елементарні дільники.
знайти її елементарні дільники.
Розв’язання
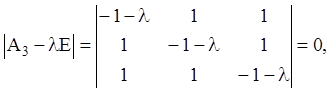
![]()
Простому характеристичному числу ![]() відповідає
простий елементарний дільник (l– 1). Для двократного характеристичного числа
відповідає
простий елементарний дільник (l– 1). Для двократного характеристичного числа
![]() ранг матриці
ранг матриці
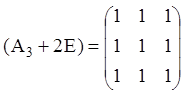
дорівнює 1, отже, число
елементарних дільників ![]() Тому елементарними
дільниками матриці будуть l–1, l+2, l+ 2.
Тому елементарними
дільниками матриці будуть l–1, l+2, l+ 2.
Приклад 4. Нехай дана
діагональна матриця 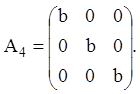
Тоді характеристичне рівняння має вигляд:
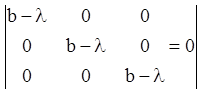
або
![]()
Тут ![]() – трикратне характеристичне число, причому
– трикратне характеристичне число, причому
![]() тому що
тому що ![]() є
нульовою матрицею. Тому число елементарних дільників
є
нульовою матрицею. Тому число елементарних дільників ![]() ,
і всі вони прості
,
і всі вони прості ![]()
Приклад 5. Дано матрицю:
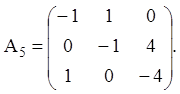
Її характеристичне рівняння ![]() тобто:
тобто:
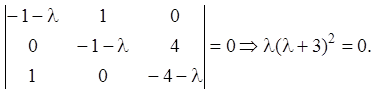
Тут ![]() – просте характеристичне число й
– просте характеристичне число й ![]() – двократне характеристичне число. Ранги
матриць:
– двократне характеристичне число. Ранги
матриць:
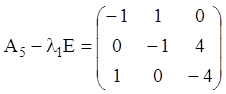 і
і 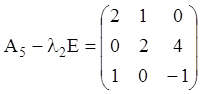 -
- ![]()
Тоді, з огляду на те, що n = 3, знаходимо, що число елементарних
дільників, що відповідають кожному характеристичному числу ![]() дорівнює
дорівнює ![]()
![]() Отже, елементарними дільниками матриці
Отже, елементарними дільниками матриці ![]() будуть lі
будуть lі
![]()
Приклад 6. Дано
матрицю: 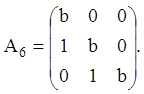
Її характеристичне рівняння:
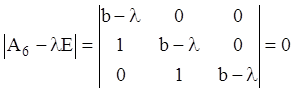 або
або ![]() має
трикратне характеристичне число
має
трикратне характеристичне число ![]() Ранг матриці
Ранг матриці 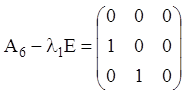 дорівнює двом
дорівнює двом ![]() , тому
число елементарних дільників, що відповідають
, тому
число елементарних дільників, що відповідають ![]() буде
буде ![]() Таким чином елементарний дільник матриці
Таким чином елементарний дільник матриці ![]() має вигляд
має вигляд ![]()
Приклад 7. Дано
матрицю 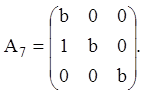
Її характеристичне рівняння ![]() або
або 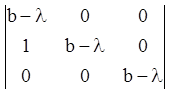 , або має характеристичне число
, або має характеристичне число ![]() в кратності 3. Ранг матриці
в кратності 3. Ранг матриці 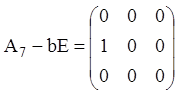 дорівнює
дорівнює ![]() . Отже,
число елементарних дільників
. Отже,
число елементарних дільників ![]() , і вони мають вигляд (l – b),
, і вони мають вигляд (l – b),![]()
Побудуємо для заданої квадратної матриці A подібну матрицю в нормальної жорданової формі (2.31). При цьому вважаємо, що числове поле K - комплексне, і елементарні дільники мають вигляд:
![]() (j = 1,2,…,u)... (2.33)
(j = 1,2,…,u)... (2.33)
де ![]() –
характеристичні числа.
–
характеристичні числа.
Розглянемо один з елементарних дільників цього виду
![]()
і поставимо йому у відповідність наступну квадратну матрицю p-го порядку:
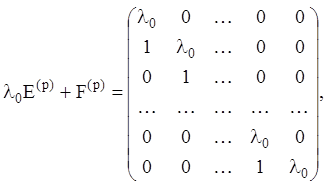 (2.40)
(2.40)
називану «нижньої» жордановою
кліткою, що відповідає цьому елементарному дільнику. Можна показати й зворотне,
що матриця (2.40) має лише один елементарний дільник ![]()
Позначимо «нижні» жорданові клітки, що відповідають елементарним
дільникам (2.33), через ![]() (j=1,2,…,u)... Тоді
квазідіагональна матриця n-го порядку структури
(j=1,2,…,u)... Тоді
квазідіагональна матриця n-го порядку структури ![]() :
:
![]()
має своїми елементарними дільниками степеня (2.33) і називається жордановою нормальною формою матриці A.
Матрицю J можна ще записати так:
![]()
![]() .
.
Жорданова форма характеризується квазідіагональним видом і структурою (2.40) діагональних кліток. Оскільки матриці A й J мають ті самі елементарні дільники, то вони подібні між собою, тобто існує деяка неособлива матриця U така, що
![]() (2.41)
(2.41)
Так, наприклад, жорданова матриця J з елементарними дільниками ![]() має вигляд:
має вигляд:
 .
.
Якщо всі елементарні дільники матриці A першого степеня, то в цьому випадку жорданова матриця є діагональною й
![]() (2.42)
(2.42)
Таким чином нормальна жорданова форма розглянутих матриць (їхня клітинна структура уздовж головної діагоналі) повністю визначається структурою елементарних дільників. Згідно (2.40), (2.41), для побудови подібної матриці в жорданової формі потрібно лише знання всіх елементарних дільників матриці A. Кожному елементарному дільнику потрібно побудувати відповідну жорданову клітку («нижню»), а по них і подібній матриці в жорданової формі.
Розглянемо кілька прикладів на приведення заданих матриць до жорданової форми, використовуючи приклади 1-7.
Приклад 8. З огляду
на, що елементарні дільники матриці ![]() (приклад 1) прості: l, l–1, l+1, жорданова форма
матриці
(приклад 1) прості: l, l–1, l+1, жорданова форма
матриці ![]() буде мати вигляд
буде мати вигляд
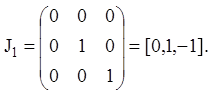
Приклад 9. Тому що
елементарними дільниками матриці ![]()
![]() (приклад
2) є
(приклад
2) є ![]() то нормальна жорданова форма матриці
то нормальна жорданова форма матриці ![]() буде квазідіагональною:
буде квазідіагональною:
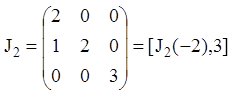
структури {2,1}.
Приклад 10.
Елементарні дільники матриці ![]() (приклад 3) прості:
(приклад 3) прості:
![]() .
.
Нормальна жорданова форма запишеться:
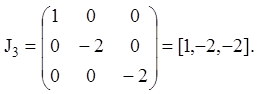
Приклад 11. З огляду
на, що елементарні дільники матриці ![]() (приклад 4) прості (l–b);(l–b);(l–b), то жорданова
форма матриці
(приклад 4) прості (l–b);(l–b);(l–b), то жорданова
форма матриці ![]() буде мати вигляд
буде мати вигляд
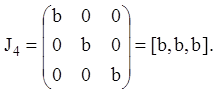
Приклад 12. Тому що
елементарні дільники матриці ![]() (приклад 5) мають вигляд
lі
(приклад 5) мають вигляд
lі ![]() то жорданова форма матриці
то жорданова форма матриці ![]() буде квазідіагональною:
буде квазідіагональною:
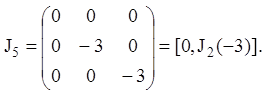
Приклад 13. Тому що елементарний дільник матриці ![]() (приклад
6) має вигляд
(приклад
6) має вигляд ![]() то жордановою формою цієї матриці
буде матриця:
то жордановою формою цієї матриці
буде матриця:
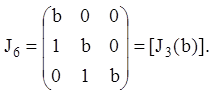
Приклад 14. З огляду
на те, що елементарні дільники матриці ![]() (приклад
7) мають вигляд
(приклад
7) мають вигляд ![]() нормальна жорданова форма цієї
матриці запишеться:
нормальна жорданова форма цієї
матриці запишеться:
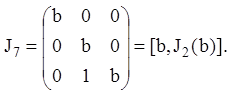
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.