якщо ![]() –
недіагональні квадратні матриці відповідних порядків
–
недіагональні квадратні матриці відповідних порядків ![]()
![]() головні діагоналі яких складають головну
діагональ всієї матриці A, а всі елементи матриці A, не приналежним матрицям
головні діагоналі яких складають головну
діагональ всієї матриці A, а всі елементи матриці A, не приналежним матрицям ![]() , дорівнюють нулю.
, дорівнюють нулю.
Алгебраїчні операції з діагональними й квазідіагональними матрицями
мають свою специфіку. Якщо ![]() й
й ![]() ,то:
,то:
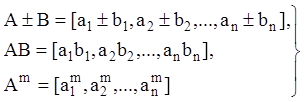 (2.21)
(2.21)
Якщо ![]() ,
, ![]() –
квазідіагональні матриці n-го порядку однакової структури, то маємо:
–
квазідіагональні матриці n-го порядку однакової структури, то маємо:
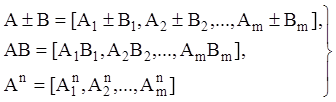 (2.22)
(2.22)
Нульовою степінню матриці ![]() називають одиничну матрицю того ж порядку,
тобто
називають одиничну матрицю того ж порядку,
тобто ![]() .
.
Операція транспонування добутку матриці здійснюється за правилом:
![]() (2.23)
(2.23)
Цілою від’ємною степінню матриці A називається ціла додатна
степінь зворотної матриці ![]() , тобто:
, тобто:
![]()
Укажемо деякі властивості визначників матриць:
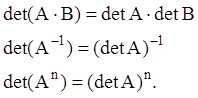
Многочленною квадратною матрицею або l - матрицею називається матриця ![]() , елементи якої є
многочленами від l:
, елементи якої є
многочленами від l:
![]() ,
(2.24)
,
(2.24)
де p – найвища степінь
многочленів ![]() .
.
Позначимо через ![]() найбільший загальний
дільник всіх мінорів j-го порядку матриці
найбільший загальний
дільник всіх мінорів j-го порядку матриці ![]() (j =
1,2,…,n)... У кожному
(j =
1,2,…,n)... У кожному ![]() беремо старший коефіцієнт, рівним
одиниці. Тоді в ряді
беремо старший коефіцієнт, рівним
одиниці. Тоді в ряді
![]()
кожен многочлен ділиться без залишку на наступний. Позначимо відповідні частки найбільших загальних дільників мінорів так :
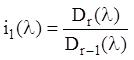 ,
, 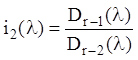 , … ,
, … , 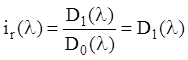 (2...25)
(2...25)
Многочлени ![]() обумовлені формулами (2.25),
називаються інваріантними многочленами квадратної l-матриці
обумовлені формулами (2.25),
називаються інваріантними многочленами квадратної l-матриці ![]()
Елементарними операціями над многочленною матрицею вважають:
1) множення k-го рядка (або стовпця) на число ![]() ;
;
2) додавання до якогось k-го рядку (або стовпцю) l-го рядку (або
стовпця), попередньо помножених на довільний многочлен ![]() ;
;
3) перестановка місцями k-го й l-го рядків (або стовпців).
Дві матриці ![]() й
й ![]() називаються
еквівалентними, якщо одна з них виходить із інший шляхом застосування
елементарних операцій. Має місце наступна теорема:
називаються
еквівалентними, якщо одна з них виходить із інший шляхом застосування
елементарних операцій. Має місце наступна теорема:
Многочленна
квадратна матриця ![]() завжди
еквівалентна канонічній діагональній матриці:
завжди
еквівалентна канонічній діагональній матриці:
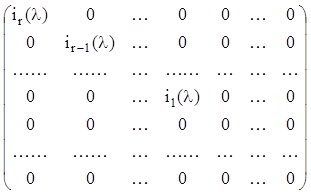 , (2.26)
, (2.26)
де r – ранг, а
![]() – інваріантні многочлени матриці
– інваріантні многочлени матриці ![]() .
.
Таким чином, інваріантні многочлени залишаються незмінними при переході
от однієї матриці к іншій, їй еквівалентній. Разкладемо інваріантні многочлени ![]() матриці
матриці ![]() на
неприводимі в даному числовому полі K множники:
на
неприводимі в даному числовому полі K множники:
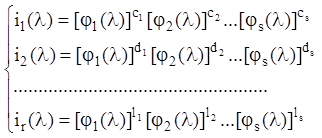 (2.27)
(2.27)
![]() k = 1,2,…,s,
k = 1,2,…,s,
де ![]() (i
= 1,2,…,s) – всі різні, що не приводять у поле K многочлени (зі старшими коефіцієнтами,
рівними одиниці), причому деякі з показників
(i
= 1,2,…,s) – всі різні, що не приводять у поле K многочлени (зі старшими коефіцієнтами,
рівними одиниці), причому деякі з показників ![]() можуть
дорівнювати нулю.
можуть
дорівнювати нулю.
Всі відмінні від одиниці степені ![]() многочленів,
що не приводять, у розкладанні (2.26) називаються елементарними дільниками
матриці
многочленів,
що не приводять, у розкладанні (2.26) називаються елементарними дільниками
матриці ![]() в поле K.
в поле K.
Для матриці ![]() до складу
до складу ![]() й наступних
й наступних ![]() (i = n –
1,…,1) будуть входити для різних характеристичних чисел
(i = n –
1,…,1) будуть входити для різних характеристичних чисел ![]() (k
= 1,2,…,u<n) множники виду
(k
= 1,2,…,u<n) множники виду ![]() . Отже, інваріантні
многочлени:
. Отже, інваріантні
многочлени:
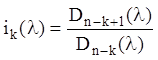 (k = 1,…,n)
(k = 1,…,n)
у своєму складі можуть мати
лише множники виду ![]() , які називають елементарними
дільниками.
, які називають елементарними
дільниками.
Розглянемо питання побудови для заданої квадратної матриці A подібної
матриці в нормальної жорданової формі. Нехай U – деяка невироджена матриця ![]() . Тоді перетворення
. Тоді перетворення
![]() (2.28)
(2.28)
яке визначає матрицю B по заданій матриці A називається перетворенням подоби з матрицею подоби U, а матриці A й B називаються подібними. Для розв'язання поставленої задачі будемо використати теорему:
Для того щоб дві квадратні матриці ![]() й
й ![]() були подібні
були подібні ![]() , необхідно
й досить, щоб вони мали ті самі інваріантні многочлени або, що ті ж саме, ті
самі елементарні дільники в поле K .
, необхідно
й досить, щоб вони мали ті самі інваріантні многочлени або, що ті ж саме, ті
самі елементарні дільники в поле K .
Нехай, задано квадратну матрицю ![]() n-го
порядку із числовими коефіцієнтами з поля K. Знайдемо елементарні дільники
матриці й позначимо їх
n-го
порядку із числовими коефіцієнтами з поля K. Знайдемо елементарні дільники
матриці й позначимо їх
![]() (2.29)
(2.29)
а відповідні супровідні
матриці – через ![]() .
.
Супровідною матрицею для многочлена
![]()
називають квадратну матрицю порядку m виду:
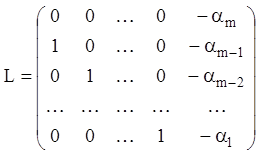 (2.30)
(2.30)
Обчисливши характеристичний многочлен матриці L переконаємося, що він
збігається з многочленом ![]() Тому що
Тому що ![]() – єдиний елементарний дільник матриці
– єдиний елементарний дільник матриці ![]() (i = 1,2,…,n), то квазідіагональна матриця:
(i = 1,2,…,n), то квазідіагональна матриця:
![]() (2.31)
(2.31)
має своїми елементарними
дільниками многочлени (2.29), тобто елементарні дільники матриці A. Тоді в силу
сформульованого критерію подоби, матриці A і ![]() подібні,
тобто завжди існує така невроджена матриця U, що:
подібні,
тобто завжди існує така невроджена матриця U, що:
![]() (2.32)
(2.32)
Матрицю ![]() називають нормальною формою
матриці A, що характеризується:
називають нормальною формою
матриці A, що характеризується:
1) квазідіагональним видом (2.31);
2) спеціальною структурою діагональних кліток (2.30);
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.