Матричний метод розв'язання однорідних лінійних систем з постійними коефіцієнтами, страница 5

Розглянемо питання приведення до канонічного виду за допомогою матричного методу лінійної однорідної системи з постійними коефіцієнтами. Нехай дана лінійна однорідна система (2.101) з матрицею коефіцієнтів . Тоді відповідне їй матричне рівняння має вигляд (2.102), де :

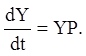                                                       (2. 117)

Введемо замість інтегральної матриці Y нову інтегральну матрицю Z за допомогою підстановки:

Z = YU,                                                        (2.118)

де U - невироджена постійна матриця. Диференціюючи (2.118) по t з урахуванням (2.117), одержуємо:

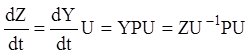
або:

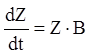                                                          (2. 119)

де:

                                                         (2. 120)

матриця, подібна до матриці P з матрицею подоби .

Виберемо тепер матрицю U так, щоб матриця B мала жорданову нормальну форму, тобто:

                                    (2. 121)

Тоді підстановкою (2.118) приведемо рівняння (2.117) до виду:

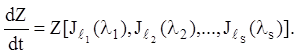                                     (2. 122)

Рівняння (2.122) називається рівнянням канонічного виду, що відповідає даному рівнянню (2.117). Інтегральною матрицею матричного рівняння (2.122) буде, згідно (2.95), матриця:

                 (2. 123)

Тоді інтегральна матриця Y даного матричного рівняння (2.117) відповідно до (2.118) має вигляд:

,                                                        (2.124)

де Z - квазідіагональна матриця (2.123), тобто має вигляд (2.112).

Цим самим визначається фундаментальна система розв'язань даної системи (2.101), що складається з s груп розв'язань структури (2.115). Система диференціальних рівнянь, що відповідає матричному рівнянню канонічного виду (2.124), називається канонічним видом даної системи (2.101).

Розглянемо тепер канонічний вид системи диференціальних рівнянь, що відповідає матричному рівнянню (2.122), з огляду на при цьому, що перехід від системи рівнянь до матричного рівняння й навпаки супроводжується транспонуванням матриці коефіцієнтів системи. Тому, транспонуючи матрицю

матричного рівняння (2.122), замість останнього одержимо відповідну систему диференціальних рівнянь або ж рівносильне їй векторно-матричне рівняння виду:

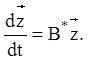                                                        (2. 125)

Якщо врахувати (2.40), можна легко встановити структуру складових частин (верхніх жорданових кліток) матриці й структуру її в цілому. Очевидно, що:

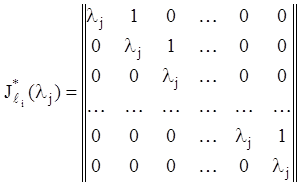,                                         (2.126)

і тому, записуючи векторно-матричне рівняння (2.125) у координатній формі, одержимо наступний канонічний вид вихідної системи (2.101):

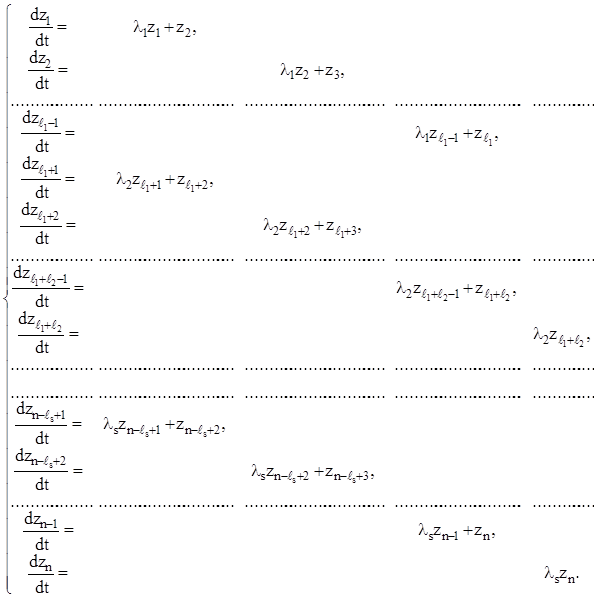
Дамо останній системі номер (2.127).

Отже, канонічним видом системи (2.101) є однорідна система n лінійних рівнянь (2.125), що складається з s груп. З огляду на те, що матриця B, обумовлена виразом (2.120), подібна до транспонованої матриці коефіцієнтів P системи (2.101), укладаємо про рівність елементарних дільників цих матриць. Тому, можна сказати, що канонічна система рівнянь (2.127) розбивається на таку кількість груп рівнянь, що дорівнює числу s всіх елементарних дільників матриці P, а число рівнянь кожної групи дорівнює степеня елементарного дільника, що відповідає цій групі. Структура канонічної системи рівнянь (2.127) наочна: діагональні коефіцієнти в кожній групі рівнянь рівні відповідному характеристичному числу, а коефіцієнти, що стоять у кожній групі на паралельній верхній діагоналі, рівні одиниці, все-таки інші коефіцієнти дорівнюють нулю.

Відзначимо, що у випадку простих елементарних дільників (це має місце завжди при простих характеристичних числах матриці P, а також може бути й при кратних характеристичних числах цієї матриці) матриця B має діагональний вигляд:

,                                                     (2.128)

а векторно-матричне рівняння (2.125) запишеться так:

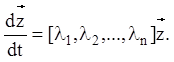                                                        (2. 129)