Відзначимо, що з теореми існування й одиничності розв'язань для систем
лінійних рівнянь, обумовлених початковими значеннями шуканої функції, випливає
за умови неперервності матриці коефіцієнтів P = P(t) на інтервалі (a, b)
існування єдиної інтегральної матриці Y(t), що задовольняє початковій умові.
(2.85). При цьому існуюча інтегральна матриця Y(t) буде визначена й неперервна
на всьому інтервалі (a, b), а за початкове значення матриці ![]() можна вибирати будь-яку постійну
невироджену матрицю.
можна вибирати будь-яку постійну
невироджену матрицю.
Розглянемо деякі властивості інтегральних матриць лінійних однорідних систем.
1. Якщо матриця ![]() є інтегральною матрицею
рівняння (2.84), то матриця
є інтегральною матрицею
рівняння (2.84), то матриця ![]() де
де ![]() – довільна постійна невироджена матриця
– довільна постійна невироджена матриця ![]() теж є інтегральною матрицею цього рівняння.
теж є інтегральною матрицею цього рівняння.
Справді, продиференціємо матрицю ![]() по t, з
огляду на, що
по t, з
огляду на, що 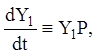 одержимо:
одержимо:
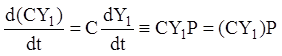
або
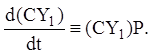 (2.86)
(2.86)
З останнього маємо, що матриця ![]() є
інтегральна матриця рівняння (2.84).
є
інтегральна матриця рівняння (2.84).
2. Якщо на інтервалі (a, b) неперервності матриці коефіцієнтів P(t)
рівняння (2.84) відома інтегральна матриця ![]() , то всі
інтегральні матриці, зазначені на цьому інтервалі, виражаються формулою:
, то всі
інтегральні матриці, зазначені на цьому інтервалі, виражаються формулою:
![]() (2.87)
(2.87)
де C - довільна постійна невироджена матриця.
Дійсно, нехай ![]() – інтегральна матриця рівняння
(2.84), що задовольняє початковій умові
– інтегральна матриця рівняння
(2.84), що задовольняє початковій умові ![]() де
де ![]() – будь-яка невироджена матриця. Покажемо,
що розглянута інтегральна матриця
– будь-яка невироджена матриця. Покажемо,
що розглянута інтегральна матриця ![]() може бути отримана з
інтегральної матриці Y, обумовленою формулою (2.87), що відповідає вибором
постійної матриці C. Для цього покладемо в (2.87)
може бути отримана з
інтегральної матриці Y, обумовленою формулою (2.87), що відповідає вибором
постійної матриці C. Для цього покладемо в (2.87) ![]() і
і ![]() . Тоді:
. Тоді:
![]()
звідки:
![]() (2.88)
(2.88)
Підставляючи знайдене значення C в (2.87), одержимо:
![]()
Тому що ця матриця й матриця ![]() мають ті саме початкове
значення
мають ті саме початкове
значення ![]() , то, у силу теореми одиничності, вони
збігаються:
, то, у силу теореми одиничності, вони
збігаються:
![]()
тобто, ![]() міститься в (2.87) при C, обумовленою
формулою (2.88).
міститься в (2.87) при C, обумовленою
формулою (2.88).
Із проведеного доказу, зокрема з матричної рівності:
![]()
маємо, що будь-яка
інтегральна матриця Y(t) виражається через відому нормовану в точці ![]() інтегральну матрицю по формулі:
інтегральну матрицю по формулі:
![]() (2.89)
(2.89)
Із другої властивості інтегральних матриць, зокрема, з формули (2.87),
маємо, що між різними фундаментальними системами розв'язань відповідної
лінійної однорідної системи (2.76) існує зв'язок, обумовлена формулою (2.87),
де ![]() й всі фундаментальні системи можуть бути
отримані з однієї відомої фундаментальної системи розв'язань.
й всі фундаментальні системи можуть бути
отримані з однієї відомої фундаментальної системи розв'язань.
Задача побудови інтегральної матриці, у загальному випадку матриці коефіцієнтів P(t), є практично нездійсненною задачею. Коротко зупинимося на окремому випадку Лаппо-Данилевського, коли матриця коефіцієнтів P(t) комутирує зі своїм інтегралом
![]() (2.90)
(2.90)
Цей випадок практично важливий тим, що задача побудови інтегральної матриці здійснюється порівняно просто для нього, і результати безпосередньо поширюються на однорідні лінійні системи з постійними коефіцієнтами.
У розглянутому випадку за інтегральну матрицю візьмемо нормовану в
точці ![]() матрицю:
матрицю:
![]() (2.91)
(2.91)
Матриця, що ![]() находиться в показнику
експонентної функції (2.91), комутирує, згідно (2.90), зі своєї похідної
находиться в показнику
експонентної функції (2.91), комутирує, згідно (2.90), зі своєї похідної 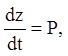 тому застосовуємо формулу диференціювання
(2.64). Тоді, диференціюючи (2.91), одержуємо:
тому застосовуємо формулу диференціювання
(2.64). Тоді, диференціюючи (2.91), одержуємо:
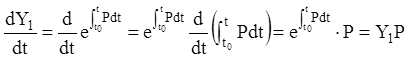
або
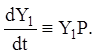 (2.92)
(2.92)
Розглянемо тепер випадок ![]() тобто розглянемо
лінійну однорідну систему диференціальних рівнянь із постійними коефіцієнтами.
Матричне рівняння (2.84) у цьому випадку приймає вид:
тобто розглянемо
лінійну однорідну систему диференціальних рівнянь із постійними коефіцієнтами.
Матричне рівняння (2.84) у цьому випадку приймає вид:
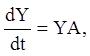 (2.93)
(2.93)
де постійна матриця ![]() задовольняє умові (2.90). Тому інтегральною
матрицею, згідно (2.91) і (2.17), буде матриця:
задовольняє умові (2.90). Тому інтегральною
матрицею, згідно (2.91) і (2.17), буде матриця:
![]() (2.94)
(2.94)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.