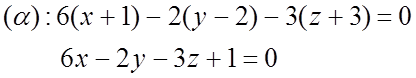
2) Найдём точку пересечения прямой (l) и пл. (a)
![]()
Прямую (l) запишем параметрическими уравнениями
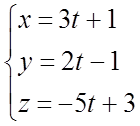 тогда,
6(3t + 1) –2(2t - 1) –3(-5t + 3) = 0
тогда,
6(3t + 1) –2(2t - 1) –3(-5t + 3) = 0
29t = 0; t = 0 Þ A(1;-1;3)
3)
Cоставим уравнение прямой ![]() , как проходящей через две точки M1 и A.
, как проходящей через две точки M1 и A.
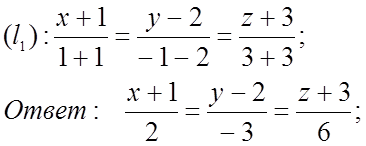
Практическое занятие № 14. Прямая и плоскость в пространстве.
1)![]() (A;B;C) – нормальный
вектор плоскости.
(A;B;C) – нормальный
вектор плоскости.
![]() -
направляющий вектор прямой.
-
направляющий вектор прямой.
2)Условие ||
(l) и (a): ![]()
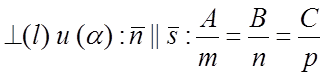
3)Угол ![]()
![]()
![]()

![]()
![]()
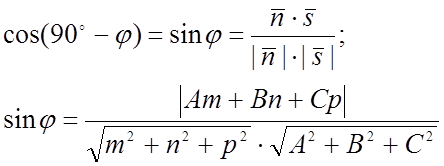
Решение задач.
№ 1040(1), 1053, 1062, 1065, 1072, 1083(1).
Д.з. № 1052, 1063(3), 1068, 1077, 1082.
№ 1040.
Найти точку пересечения прямой 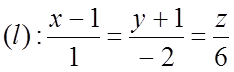 и
плоскости
и
плоскости
![]()
1)
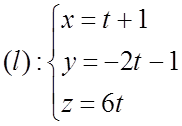
2) 2(t + 1) +3(-2t -1) +6t –1 = 0; 2t – 6t + 6t +2 – 3 –1 = 0
2t – 2 = 0 t = 1 Þ M(2;-3;6)
№ 1053.
![]()

P(5;2;-1)
(a): 2x – y
+ 3z + 23 = 0 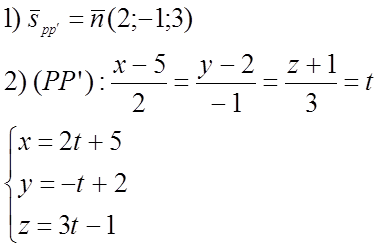
3)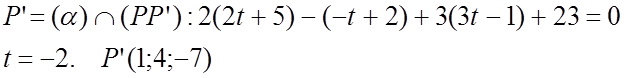
№ 1062
Вычислить
расстояние d от точки
P(1;-1;-2) до прямой 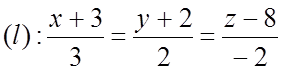
P(1;-1;-2) 1) Возьмём на прямой(l)
![]()
![]()

 произвольную т. М .Пусть М(-3;-2;8)
произвольную т. М .Пусть М(-3;-2;8)
d=h
![]()
![]()
![]()
M(-3;-2;8)
Пусть
направляющий вектор прямой (l) ![]() приложен
к т. М.
приложен
к т. М.
2) Найдём
векторное произведение [![]() ]
]
![]()
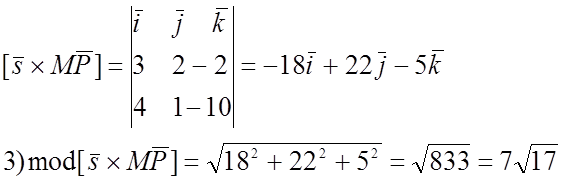
а это есть площадь параллелограмма, построенного на векторах, как на сторонах.
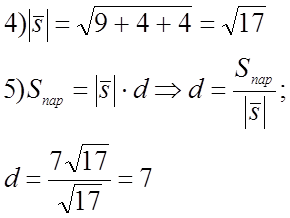
Ответ: 7 лин.ед.
№ 1065. Соствить уравнение плоскости, проходящей через т.М1(1;2;-3),
|| прямым 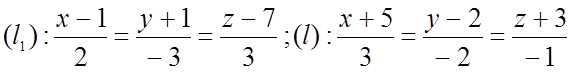
![]()




1)
Т.к. ![]() , с
помощью || переноса
, с
помощью || переноса ![]() и
и ![]() можно поместить на одну плоскость b Þ a || b
можно поместить на одну плоскость b Þ a || b
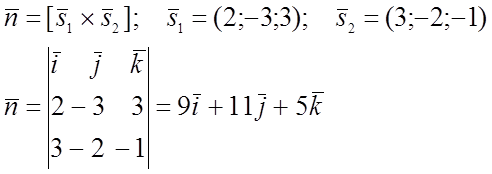
2)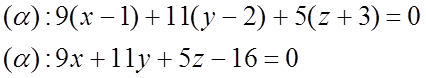
№ 1072. Составить уравнение плоскости, проходящей через две || прямые:
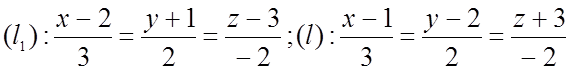
![]()
![]()
![]()
![]()



![]()
![]()
(![]() )
)
(a)
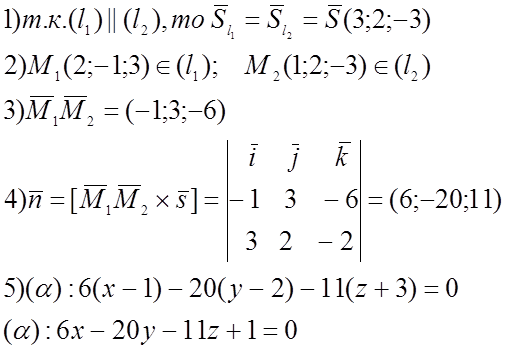
№ 1083(1). Вычислить кратчайшее растояние между двумя прямыми.
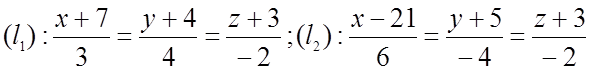
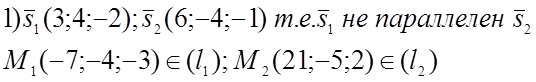
РИСУНОК.
2)
Составим уравнение пл. (a), проходящей через ![]()
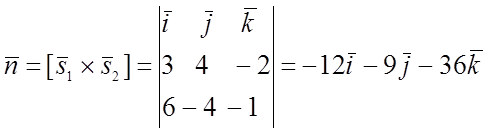
Возьмём
ему коллинеарный вектор ![]()
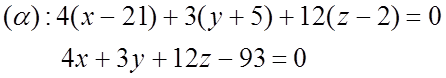
3) Найдём расстояние от точки М1 до (a):
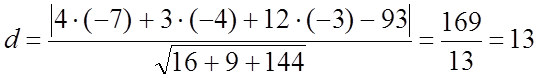
Ответ: d = 13.
Практическое занятие № 15. Кривые 2 порядка.
1) Эллипс, оружность.
2) Def: Эллипс – это гмт., для которых сумма расстояний до двух фиксированных точек плоскости, называемых фокусами, есть величина постоянная = 2a, причём большая, чем расстояние между фокусами(2а>2c).
РИСУНОК 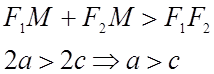
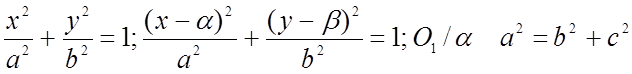
Def: Эксцентриситемом эллипса называется число 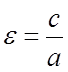 (a – большая полуось Þ a > b) e < 1.
(a – большая полуось Þ a > b) e < 1.
3)Если a < b , то уравнение то же, только фокусы находятся на оси OY.
4)Директрисами эллипса называютя прямые || OY, определяемые уравнением :
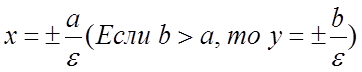
MN = d – расстояние от текущей точки до односторонней с этим фокусом директрисы.
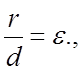 r – фокальный радиус.
r – фокальный радиус.
5)Если a = b, то имеем окружность :
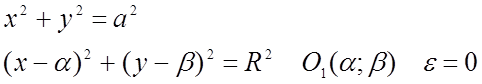
2)Гипербола
1) Def: Гипербола – г.м.т., для которых разность расстояний от двух фиксированных точек плоскости , называемыми фокусами, есть величина постоянная = 2а < 2c (a < c).
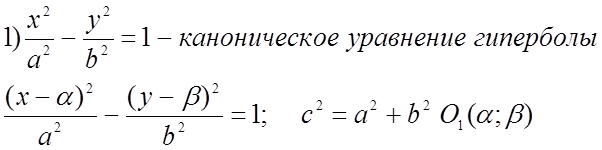
для (1) фокус на оси OX.
![]() Если фокусы лежат на оси OY ,
то
Если фокусы лежат на оси OY ,
то 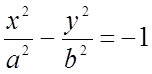 (2)
(2)


![]()
![]()

![]()
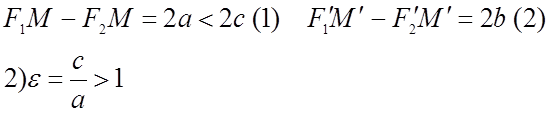
3)Гиперболы 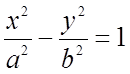 и
и 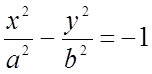 называются
сопряжёнными
называются
сопряжёнными
4)Если a = b , то гипербола называется равносторонней
![]()
Сравни: xy = k – это равносторонняя гипербола, a = 45о
5)Директрисы 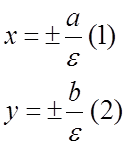
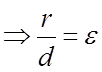
Решение задач.
№ 446(5;9), 447, 193, 455(2;3), 471(1), 472(1;3), 473(1), 397(5), 398(3;6), 194, 518, 541(1), 542(3), 546.
Д.з. № 387, 435, 448, 471(2), 472(2;4), 544, 546, 542(1;2;4).
ЭЛЛИПС.
№ 446(5)
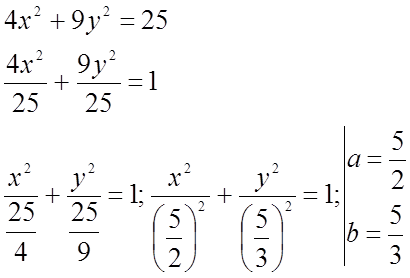
№ 446(9).
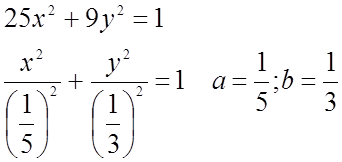
№
447.![]()
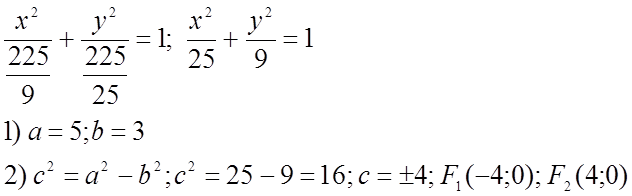
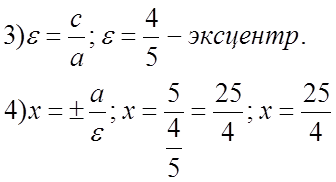
директрисы:
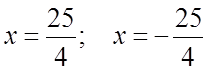
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.