Линейные неоднородные уравнения. Методы решения неоднородных линейных уравнений, страница 2

9.2.2 Решение неоднородных линейных дифференциальных уравнений с постоянными коэффициентами и со специальной правой частью

НЛДУ с постоянными коэффициентами имеет вид:

     (9.20)

где  – непрерывная функция.

Поскольку соответствующее однородное уравнение всегда можно решить, то предложенный выше метод вариации произвольных постоянных можно всегда использовать для нахождения частных решений уравнения (9.20). Но метод вариации имеет существенные недостатки: решение алгебраической системы с довольно сложными коэффициентами, вычисление громоздких интегралов. Поэтому, если возможно, его избегают и применяют так называемый метод неопределенных коэффициентов, который позволяет при определенной структуре правой части уравнения (9.1) найти его частные решения без квадратур (этот метод называют еще методом подбора частного решения). В таких случаях, складывая это частное решение с общим решением соответствующего однородного уравнения, получаем без квадратур и общее решение уравнения (9.20).

Общий вид специальной правой части, для которой применим метод неопределенных коэффициентов, следующий:

               (9.21)

где -многочлены степени  и  соответственно,  В этом случае частное решение неоднородного уравнения ищем в виде «похожем» на :

            (9.22)

где  и  – многочлены с неопределенными коэффициентами степени ;  -кратность характеристики правой части числа  среди корней характеристического уравнения. Число  будем называть характеристической специальной правой части. Если число  не встречается среди корней характеристического уравнения, то полагают . Под многочленами  и  понимают:

 

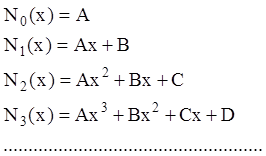
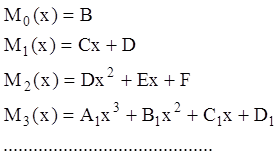
Коэффициенты полиномов  и  определяем непосредственной подстановкой  (9.22) в уравнение (9.20) и приравниванием коэффициентов при подобных членах в левой и правой части полученного равенства. Искомые коэффициенты найдутся, и при этом единственным образом, так что уравнение (9.20) имеет только одно частное решение.

В частности, если в уравнении (9.1) правая часть  представляет собой произведение полинома на показательную функцию (частный случай общей:

                                 (9.23)

специальной правой части (9.21) при ), где

,        (9.24)

 (или множеству комплексных чисел). При построении частного решения (9.22), различают два случая.

Если число  не является корнем характеристического уравнения

Тогда из (9.22)  и :

,                       (9.25)

где

     (9.26)

есть многочлен - й степени с неопределенными коэффициентами, так что частное решение имеет ту же аналитическую структуру, что и правая часть самого уравнения (9.23).

Если же  является - кратным корнем характеристического уравнения т.е.  то из (9.22) следует, что  будет иметь вид:

                                                                                                    (22)

где  имеет вид (9.26).

Коэффициенты полиномов (9.26) определяется подстановкой (9.25) и соответственно (9.27) в уравнение (9.1). Непосредственной подстановкой убеждаемся, что искомые коэффициенты находятся и притом единственным образом, так что уравнение (9.1) имеет только одно частное решение вида (9.25) или (9.27).

П р и м е р  2. Найти общее решение уравнения

Р е ш е н и е. Общее решение этого уравнения ищем в виде .

1. Ищем : . Записываем соответствующее характеристическое уравнение: .  или ; . Тогда .

2. Ищем : в нашем случае . Сравнивая эту функцию с общим видом специальной правой части  (9.21), находим, что . И из (9.22) находим:

 , т.е. . Подставляем  в исходное уравнение, предварительно вычислив:

.

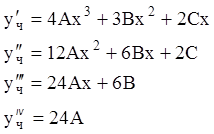Получаем  или

.

Приравниваем коэффициенты при подобных членах, получаем

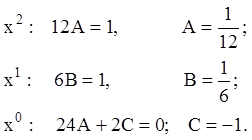
Тогда искомое частное решение и, соответственно, общее решение неоднородного уравнения запишутся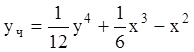

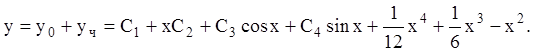
П р и м е р  3. .

; ; ; ;  и из (9.22) записываем:

 .

Для нахождения  вычисляем  и  и подставляем в неопределенное уравнение:

 

;

 .

Подставляем в уравнение:

  ;

.

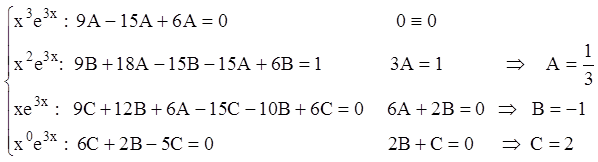И, таким образом, 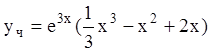. Общее решение неоднородного уравнения: .

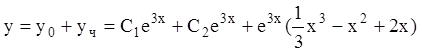П р и м е р  4. .

 

; ;

.

Сравнивая это  с самым общим видом (9.21) находим, что:

, т.к.  и

Тогда из (9.22): . Вычисляем производные:

 

 

.

Подставляем в уравнение:

.

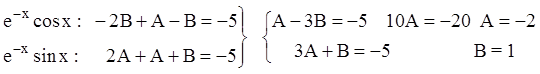Тогда  и общее решение неоднородного уравнения запишется:  Для нахождения решения задачи Коши предварительно вычисляем:

Тогда из начальных условий получаем:

.

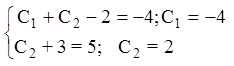Искомое частное решение запишется:

.

З а м е ч а н и е. При нахождении частных решений неоднородных линейных уравнений удобно пользоваться следующим свойством линейного уравнения.

Если  являются решениями уравнений соответственно:

,  (9.28)

то функция

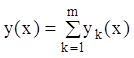                                (9.29)

является решением уравнения:

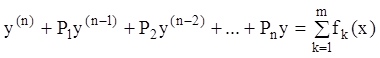.      (9.30)

Д о к а з а т е л ь с т в о почти очевидно: подставляем функцию (9.29) в уравнение (9.30) и используем при этом (9.28).

П р и м е р  5. Решить уравнение .

; ; ;

; ;

.

Тогда:

.