Застосування криволінійних інтегралів, страница 4

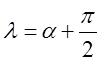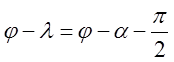Якщо,   як завжди,   означає   кут  між   дотичною  і  віссю  Ох (рис.9.3.), то дасть  кут нормалі з тією ж віссю. ( Далі застосовується теорема з шкільної геометрії: величина зовнішнього кута трикутника дорівнює сумі двох внутрішніх кутів не суміжних з ним). Тоді кут між напрямком швидкості і нормаллю буде   і 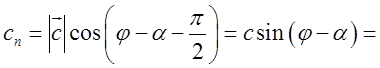(скористаємось (*)) = =. Підставивши це в (9.6), одержимо 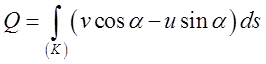. 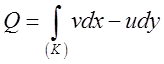Але ж , тому                                                        (9.7)

Це і є відповідь на поставлене задачею запитання, але ми продовжимо досліджувати (9.7). Звернімо увагу, що ми, обчислюючи кількість рідини, яка протече через криву (К) за одиницю часу, перейшли від (9.6) до (9.7), тобто від інтегралу першого типу до інтегралу другого типу. Це значить, що в (9.6) враховується лише кількість пройденої рідини, а в (9.7) враховується і знак – додатній це коли напрям потоку співпав з нами обраним і в протилежному випадку – від’ємний.

Важливо ще підкреслити, що напрямок інтегрування  вздовж цієї кривої повинен бути                        Рис. 9.3.                                  таким, щоб кут між відповідним напрямком дотичної  і  обраним  заздалегідь  напрямком  нормалі    дорівнював , бо саме в цьому припущенні і виведена була формула (9.7).

Якщо  (К)  є  замкнутий  контур і інтеграл  (9.7) вважати взятим, як  звичайно в   додатньому  напрямку,  то, щоб було виконано  згадану  тільки   що умову, нормаль повинна була б бути спрямована всередину  області,  обмеженої  контуром (К). Отже, в цьому випадку формула (9.7) дає кількість рідини, що протікає через контур (К) в   одиницю  часу  всередину  області.  Якщо  бажаємо одержати кількостей рідини, що  випливає  назовні  з  області, обмеженої контуром (К), то потрібно  у формулі (9.7) лише змінити знак.

Далі,  якщо  поле  не має ні «джерел», ні «стоків» рідини, то у   будь-якій  обмеженій  області  кількість рідини залишається постійною. Тому,  яку  б  замкнуту  криву  не взяти розташовану в полі потоку, інтеграл (9.7), узятий по ній, повинний  дорівнювати нулю. Отже, якщо швидкість у плоскій сталій течії  нестисливої рідини, то при відсутності джерел  і стотів 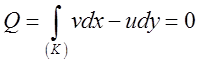 , яким  би не був замкнутий контур (К).

9.5. Задача про роботу газу, який розширяється в циліндрі

В циліндрі знаходиться газ рід тиском р. Цей газ рухає поршень від початкового пороження – точки А, до кінцевого – точки В. Обчислити роботу, яку при цьому виконує газ.

            Обчислимо диференціал роботи. Для цього виділимо переміщення поршня . Зрозуміло, що переміщення поршня звязане зі зміною обєму за лінійним законом. . Сила, яка діє на поршень дорівнює р, а тому  і якщо , то . Інтегруючи вздовж лінії переміщення поршня від А до В одержимо 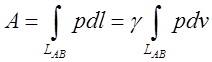                    . Це і є відповідь.

9.6. Задача про обчислення площі плоскої фігури

 В площині хОу задана плоска фігура D обмежена контуром (L)АМВNA, рис.9.4, причому вся вона лежить між променями ОВ і ОА (ці промені мають лише по одній спільній точці з L). Знайти площу вказаної фігури.

Розв’язок. Нам знадобиться з курсу аналітичної геометрії формула обчислення площі трикутника за координатами трьох його відомих вершин .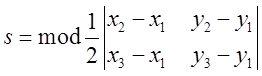

На кривій АМВ візьмемо точку P(x,y) і                                    рис.9.4.                                     сусідню з нею точку . Замінимо ділянку кривої на відрізок . (як завжди  – дуже маленьке і в подальшому воно у нас буде прямувати до 0). Площа трикутника дорівнює 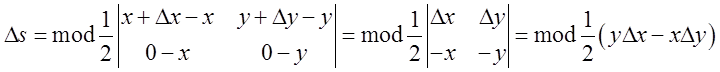. При  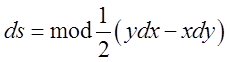і щоб знайти площу всього криволінійного сектора ОАМВО, треба знайти криволінійний інтеграл вздовж кривої АМВ від точки А до точки В. 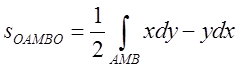  Розмірковуючи аналогічно визначимо площу криволінійного сектора ОBNAO 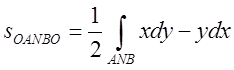. Звернім увагу на те, що в першому випадку ми брали інтеграл обходячи шукану площу в додатньому напрямку, а в другому – у відємному. Величина площ від цього не змінилась, але нам важливо щоб в обох випадках у цих площ був однаковий знак, бо площа шуканої фігури  АМВNA є різниця площ знайдених вище криволінійних секторів