Застосування кратних інтегралів

Лекція 6

Застосування кратних інтегралів

План:

 6.1. Збірка формул.

 6.2. Приклади.

 6.3. Запиння для самоперевірки.

Українсько-російський словник вжитих в лекції слів, які в мовах мають різне звучання.

Одержані –полученные Застосування –применение Користування –пользование Вигляд –вид Зведення –сводка Наступні –следующие

Відносно –относительно Відцентровий –            –центробежный Обертається –вращается Спростити –упростить Доцільно –целесобразно

Наявність –наличие Перетвориться –преобразится Спонукають –побуждают Завдяки –благодаря Розмістити –расположить Випливає –следует

Математичні факти з попередніх розділів, які використовуються в даній лекції.

1. При переході до криволінійних систем координат доведеться  перераховувати границі інтегрування. При цьому алгебраїчні нерівності типу , або  перейдуть в тригонометричні нерівності:  та  . При їх розвязуванні слід враховувати що за означенням , а  або  (про це повинна бути попередня домовленість в залежності від розташування фігури в полярній системі координат). Розв’яжемо вищенаписані нерівності. ; , далі в зв’язку з тим, що  не може бути від’ємним одержимо: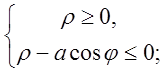розвязок системи дає границі інтегрування за змінною : .  Користуючись тим, що , при розвязку другої нерівності 

  ми маємо право провести скорочення на не змінюючи знаку нерівності. . Далі при умові, що фігура знаходиться в півплощині  і тут , ми ділимо обидві частини нерівності на  і одержуємо найпростішу тригонометричну нерівність 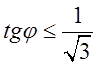. Із нескінченної множини розвязків цієї нерівності беремо лише той розвязок, який знаходиться в межах нашої фігури. В даному разі .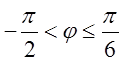

6.1. Збірка формул

Як подвійний так і потрійний інтеграли нами були одержані при розв’язуванні конкретних геометричних чи фізичних задач (об’єм та маса). Застосовуючи аналогічні міркування, одержимо ще багато формул застосування кратних інтегралів, які для  зручності користування подамо у вигляді зведення.

1.Площа плоскої фігури S: 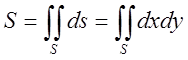                                                                (6.1)

1а. Площа поверхні , однозначна проекція, якої на площину хОу є D

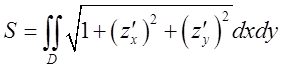                                                                                                (6.1а)

2.Обєм фігури V обмеженої циліндричною поверхнею і поверхнями: зверху ; знизу , D – область-проекція фігури V на площину ХОУ.

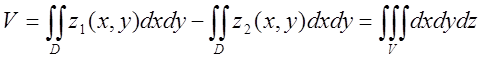                                                               (6.2)

В наступних формулах  є функція змінної густини.

3.Маса плоскої пластинки змінної  густини 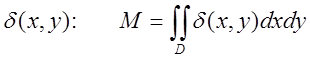.                  (6.3)

4. Маса обємного тіла V змінної  густини :  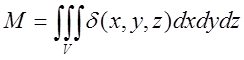      (6.4)

5.Статичні моменти пластинки: ,           (6.5)

6.Статичні моменти відносно координатних  площин неоднорідного тіла, яке  займає об’єм V: 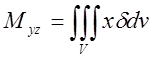  ; 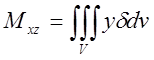;  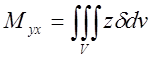.                                             (6.6)

7.Координати центру ваги пластинки: 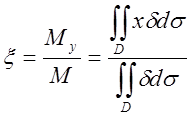; 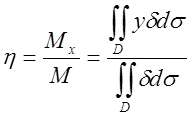(6.7)

8.Координати центра ваги  неоднорідного тіла, яке займає в просторі об'єм V: 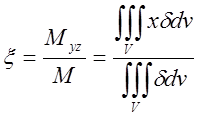;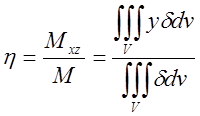: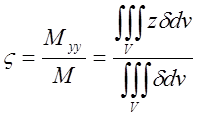.                                     (6.8)

9. Моментом інерції матеріальної точки Р з масою m відносно якої-небудь осі називається добуток  маси на квадрат віддалі точки Р до цієї осі.

Моменти  інерції пластинки із  змінною густиною  відносно координатних осей.

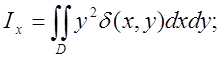
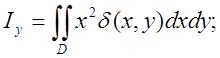                                                                     (6.9)

10. Аналогічно обчислюються моменти інерції відносно осей неоднорідного тіла з густиною , яке займає обєм V:

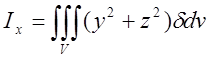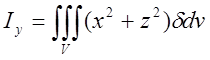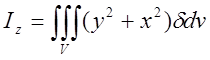; ;.                                 (6.10)                      11.Відцентровий момент інерції:  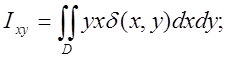                                            (6.11)

12.Полярний момент інерції:

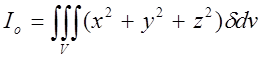;                                                 (6.12)

13.Кінетична енергія тіла, яке обертається навколо осі OZ:                      (6.13)

6.2. Приклади

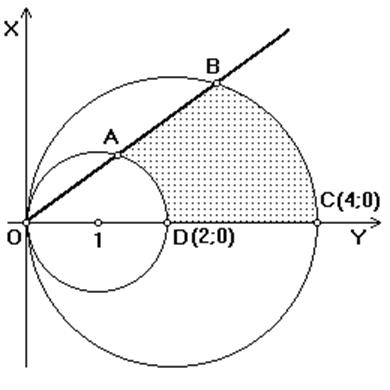П.1. Знайти площу фігури, обмежену лініями

               x²+y²=2x, x²+y²=4x, y=x, y=0.

Розв’язок. Площа фігури знаходиться за формулою 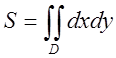. Зобразимо фігуру D обмежену заданими кривими, площу якої S треба знайти, рис. 6.1. Для цього спростимо задані рівняння кривих, якими вона обмежена:

В перших двох рівняннях виділимо повні квадрати (x-1)²+y²=1 і  (x-2)²+y²=4. Ці два кола разом з прямими  y=0  і y=x  утворюють фігуру ABCD, площу якої і треба знайти. При                             Рис. 6.1.                 

 розв`язанні доцільно перейти до полярної системи координат. Ця доцільність випливає з того, що область обмежена двома променями y=0  і y=x  (в полярній системі це будуть 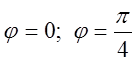 і це межі інтегрування зовнішнього інтеграла), а також із наявності в рівняннях кривих  x²+y². При переході в полярну систему координат цей вираз перетвориться в . Отож, перейдемо до полярної системи координат: x=rcosjy=rsinj.   Підставляємо ці значення x і y в початкові рівняння кривих: