![]() ,
, 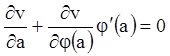
(це можна зробити тільки якщо
![]() обрано), т будемо мати огинаючу сімейства
поверхонь, що буде теж інтегральною поверхнею, тобто розв'язанням рівняння
(4.35). Сукупність всіх таких, що обгинають при довільному виборі
диференційованої функції
обрано), т будемо мати огинаючу сімейства
поверхонь, що буде теж інтегральною поверхнею, тобто розв'язанням рівняння
(4.35). Сукупність всіх таких, що обгинають при довільному виборі
диференційованої функції ![]() й становить геометричний
зміст загального інтеграла рівняння (4.35). Можна було б показати, що зазначеними
вище розв'язаннями вичерпуються всі розв'язання рівняння (4.35). Інакше кажучи,
кожен інтеграл рівняння (4.35) міститься або в повному, або загалом, або в
особому інтегралі.
й становить геометричний
зміст загального інтеграла рівняння (4.35). Можна було б показати, що зазначеними
вище розв'язаннями вичерпуються всі розв'язання рівняння (4.35). Інакше кажучи,
кожен інтеграл рівняння (4.35) міститься або в повному, або загалом, або в
особому інтегралі.
Рівняння в частинних похідних уперше (1747 р.) вивчали Ейлер і Даламбер
у зв'язку із проблемами фізики (рівняння другого порядку). Диференціальні
рівняння в частинних похідних першого порядку типу 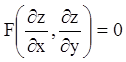 вже
зустрічаються в роботах Ейлера. В 1776 р. Лагранж дав розв'язання лінійного
рівняння
вже
зустрічаються в роботах Ейлера. В 1776 р. Лагранж дав розв'язання лінійного
рівняння
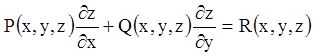
приведенням його до системи
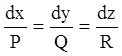 ,
,
а пізніше (1781 р.) розповсюдив той же прийом на випадок довільного числа незалежних змінних.
З вище викладеного витікає, що задачу інтегрування рівняння в частинних похідних першого порядку можна вважати формально закінченої, якщо вдається знайти її повний інтеграл, або інші розв'язання одержимо з нього диференціюванням і виключенням. Перш ніж переходити до викладу методу, що фактично дозволяє знайти повний інтеграл будь-якого рівняння першого порядку, розглянемо задачу знаходження розв'язання двох рівнянь першого порядку з однією шуканою функцією
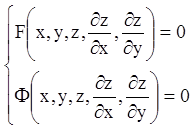 .
(4.38)
.
(4.38)
Будемо припускати, що в систему (4.38) можна розв'язати відносно 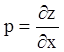 й
й 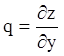 , тобто
що
, тобто
що 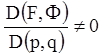 .
.
Тоді із системи (4.38) одержуємо:
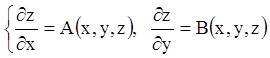 . (4.39)
. (4.39)
Два рівняння (4.38) або (4.39), які містять тільки одну шукану функцію ![]() не завжди є спільними. Далі будемо
називати систему (4.39) повністю інтегрованою, якщо вона має розв'язання,
що залежать від довільної постійної
не завжди є спільними. Далі будемо
називати систему (4.39) повністю інтегрованою, якщо вона має розв'язання,
що залежать від довільної постійної
![]() .
(4.40)
.
(4.40)
Установимо необхідні й достатні умови повної інтегрованості, а також
дамо спосіб знаходження розв'язання, якщо ця умова виконана. Покладемо, що
існує загальне розв'язання ![]() , що має неперервні
частинні похідні першого порядку й неперервну першу похідну
, що має неперервні
частинні похідні першого порядку й неперервну першу похідну 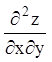 . Диференціюючи перше з рівностей (4.39) по
. Диференціюючи перше з рівностей (4.39) по
![]() , а друге по
, а друге по ![]() , будемо
мати:
, будемо
мати:
 ,
, 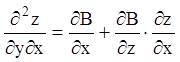
або, на підставі рівнянь (4.39) і неперервності змішаної похідної другого порядку
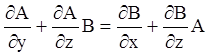 .
(4.41)
.
(4.41)
Тут, звичайно, передбачається існування й неперервність всіх чотирьох
частинних похідних, які входять в останню рівність. Якщо рівність (4.41) не є
тотожністю, то вона визначає ![]() як неявну функцію від
як неявну функцію від ![]() й
й ![]() і
тільки ця функція, що не містить довільної постійної, може бути розв'язанням
системи (4.39).
і
тільки ця функція, що не містить довільної постійної, може бути розв'язанням
системи (4.39).
Але наша мета встановити умови, при виконанні яких система (4.39) має
нескінченну множину розв'язань, і таких, що через кожну точку ![]() розглянутої області простору проходить
поверхня, що відповідає певному розв'язанню. Виходить, умова (4.41) повинне
виконуватися в кожній точці, тобто тотожно відносно
розглянутої області простору проходить
поверхня, що відповідає певному розв'язанню. Виходить, умова (4.41) повинне
виконуватися в кожній точці, тобто тотожно відносно ![]() .
.
Висновок: тотожне
виконання умови (4.41) необхідно для того, щоб система (4.39) була повністю
інтегрованої, тобто мала розв'язання, що залежить від довільної постійної (при
заданих ![]() можна підібрати довільну постійну
можна підібрати довільну постійну ![]() так, щоб
так, щоб ![]() прийняв
будь-яке значення
прийняв
будь-яке значення ![]() ).
).
Покажемо, що тотожність (4.41) є достатньою умовою. Проінтегруємо перше
з рівностей (4.39), розглядаючи ![]() як параметр, а саме
рівняння – як рівняння з однієї незалежної змінної. Будемо мати
як параметр, а саме
рівняння – як рівняння з однієї незалежної змінної. Будемо мати
![]() .
(4.42)
.
(4.42)
Ця функція повинна задовольняти й іншому з рівнянь (4.39), тобто повинна виконуватися рівність
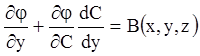
або
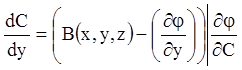 ,
(4.43)
,
(4.43)
причому в правій частині
(4.43) ![]() необхідно замінити його виразом (4.42).
Якщо (4.41) виконується тотожно, то права частина рівності (4.43) не містить
змінної
необхідно замінити його виразом (4.42).
Якщо (4.41) виконується тотожно, то права частина рівності (4.43) не містить
змінної ![]() . Дійсно, похідна правої частини (4.43) по
. Дійсно, похідна правої частини (4.43) по ![]() буде мати вигляд
буде мати вигляд
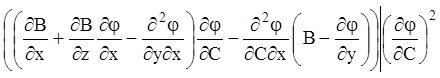 . (4.44)
. (4.44)
Але функція ![]() задовольняє першому з рівнянь
(4.39), тоді
задовольняє першому з рівнянь
(4.39), тоді
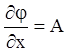 ,
, 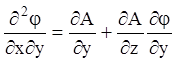 ,
, 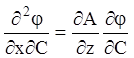 .
.
Тому (4.44) прийме вид
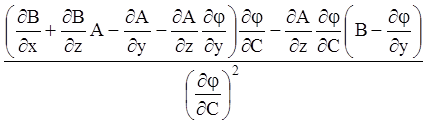 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.