реактивными
силами — силы ![]() и
и ![]() здесь же изображены эпюры
удельных давлений на передних и задних гранях направляющих в форме трапеций.
здесь же изображены эпюры
удельных давлений на передних и задних гранях направляющих в форме трапеций.
Рассматривая шпиндельную бабку, как жесткое тело, находящееся под действием нескольких сил в равновесии, составляем уравнения статики.
Уравнение проекций сил на вертикальную ось:
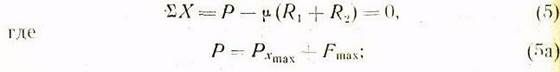
![]() —сила трения шлицевого соединения
шпинделя и гильзы коробки скоростей;
—сила трения шлицевого соединения
шпинделя и гильзы коробки скоростей;
![]() — коэффициент трения на гранях направляющих.
— коэффициент трения на гранях направляющих.
Уравнение проекций сил на горизонтальную ось Y.
![]()
Уравнение моментов сил относительно точки О:
![]()
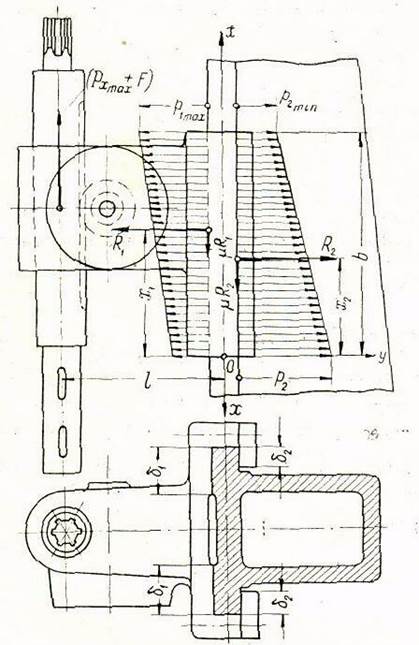
Рис. 4. Расчетная схема к определению основных размеров плоских прямоугольных направляющих. Шпиндельная бабка укреплена неподвижно на станине сверлильного станка.
|
Из уравнения (2) следует, что (1) можно записать в таком виде: |
![]()
Откуда
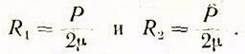
Выразим
значения ![]() в зависимости от
максимальных удельных давлений
в зависимости от
максимальных удельных давлений ![]() . Рассматривая эпюры удельных давлений на гранях
направляющих, можем написать, что
. Рассматривая эпюры удельных давлений на гранях
направляющих, можем написать, что
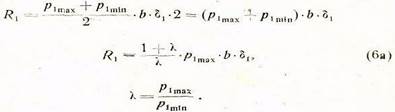
или
где
Аналогичным
образом определяется значение реакции ![]() , которая выражается формулой:
, которая выражается формулой:
![]()
Затем
определяем координаты центров давлений ![]() .
.
Для
этого обращаемся к рис. 5, где трапеция удельных давлений представлена в виде
прямоугольника и треугольника. Равнодействующие давлений частных эпюр
соответственно обозначены через ![]() , их координаты—через
, их координаты—через 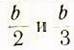 .
.
Чтобы
определить координату ![]() ,
составляем уравнение моментов сил относительно точки О, Имеем:
,
составляем уравнение моментов сил относительно точки О, Имеем:
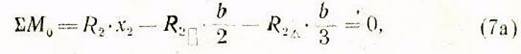
где
![]()
или
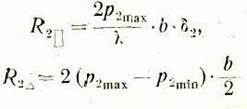
или
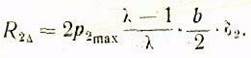
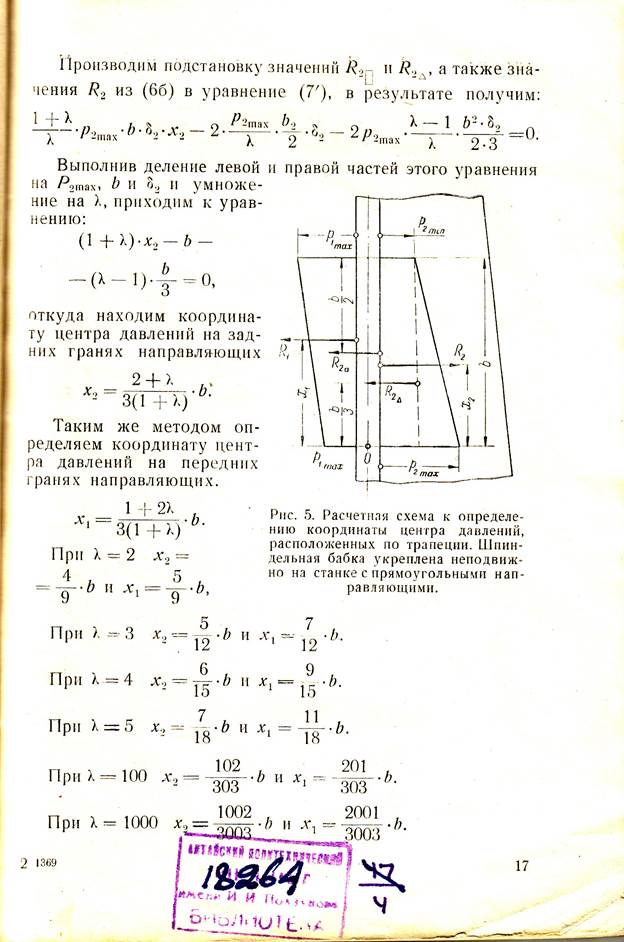
Отсюда
видно, что по мере увеличения значения ![]() трапеция приближается к
треугольнику. При
трапеция приближается к
треугольнику. При ![]() , когда
, когда ![]() и
и ![]() обращаются
в нуль, трапеции превращаются в треугольники.
обращаются
в нуль, трапеции превращаются в треугольники.
Далее выразим ![]() в зависимости от l и b.
Для этого воспользуемся уравнением (7) и подставим в него вначале
в зависимости от l и b.
Для этого воспользуемся уравнением (7) и подставим в него вначале ![]() и
и ![]() а затем
а затем![]()
Будем иметь:
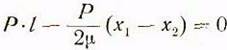
или
![]()
Подстановка ![]() дает:
дает:
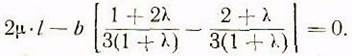
Отсюда находим:
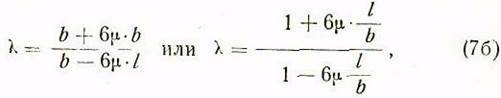
где I и b показаны на рис. 4.
Переходим к выводу формул для определения удельных давлений на гранях направляющих.
Подставляя значения ![]() из (6а) и (66) в уравнение(7),
будем иметь:
из (6а) и (66) в уравнение(7),
будем иметь:
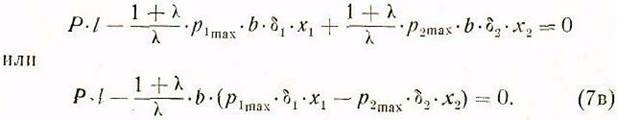
Приравниваем правые части равенств (6а) и (66) на основании уравнения (б):
![]()
или после сокращения
![]()
Учитывая это соотношение, переписываем уравнение (7в) в таком виде:
![]()
После подстановки сюда значений ![]()
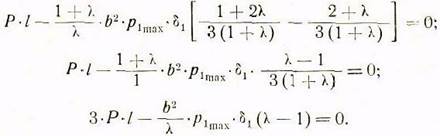
Отсюда удельное давление

и соответственно на сновании соотношения
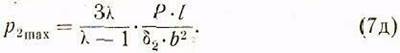
Поделив
числитель и знаменатель правых частей равенств (7г) и (7д) на ![]() и приняв
и приняв ![]()
что
соответствует нулевым значениям ![]() получим формулы для максимальных удельных
давлений на передних и задних гранях направляющих в случае распределения
таковых по закону треугольника.
получим формулы для максимальных удельных
давлений на передних и задних гранях направляющих в случае распределения
таковых по закону треугольника.
Рассматривая формулы (7г) и (7д), нетрудно заметить, что ![]() так так
так так ![]()
Поэтому расчет следует вести прежде всего основных размеров задних граней направляющих.
Обозначим
отношение ![]() в формуле (7д)
через k, то есть
в формуле (7д)
через k, то есть 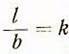 , откуда
, откуда ![]() тогда после подстановки этих величин в формулы
(76) и (7д) последние принимают такой вид:
тогда после подстановки этих величин в формулы
(76) и (7д) последние принимают такой вид:
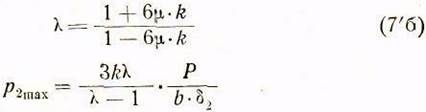
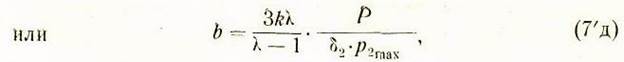
где Р объяснено выше [см. уравнения (5а)].
б) Расчет на устойчивость шпиндельной бабки
Кроме изложенного расчета удельных давлений (и определение основных размеров направляющих) необходимо произвести расчет на устойчивость шпиндельной бабки. При этом воспользуемся уравнением (5). Его можно переписать в таком виде:
![]()
где ![]() —силы трения в направляющих;
—силы трения в направляющих;
![]()
Для устойчивого равновесия шпиндельной бабки при работе станка необходимо, чтобы выполнялось условие
![]()
Коэффициентом устойчивости назовем отношение
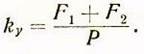
На
основании предыдущего силы трения ![]() на гранях направляющих станины в зависимости от
максимальных удельных давлений и основных размеров направляющих определяются в
таком виде:
на гранях направляющих станины в зависимости от
максимальных удельных давлений и основных размеров направляющих определяются в
таком виде:
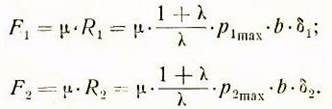
Сумма этих сил:
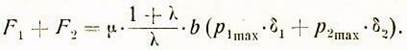
Исходя из уравнения (6), выше было показано, что
![]()
На этом основании:
![]()
После подстановки значения ![]() в правую часть последнего равенства:
в правую часть последнего равенства:
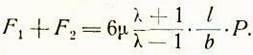
Учитывая последнее и (5), определяем коэффициент устойчивости шпиндельной бабки в таком виде:
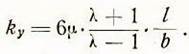
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.