Аналогично рассматриваются оставшиеся два интеграла. В результате, вычисление поверхностного интеграл 2-го рода сводится к вычислению трех двойных интегралов:
 . (4.5)
. (4.5)
Знак "плюс" здесь выбирается в том случае, если интегрирование происходит по той стороне поверхности, которая обращена в сторону положительных направлений осей Ox, Oy и Oz. Если это не так, то нужно взять знак "минус" у соответствующего интеграла.
Замечание. Следует иметь в виду, что, поверхностные интегралы 2-го рода (в соответствии с формулой (4.4)) часто записывают в виде
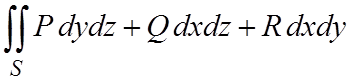 , (4.6)
, (4.6)
где P=P(x,y,z), Q=Q(x,y,z), R=R(x,y,z) – какие-то функции, заданные на поверхности S.
Пример 4.2.
Вычислить поток векторного поля a=yj через верхнюю часть плоскости x+y+z=2, лежащей в
первом октанте
(см. рис. 4.1).
|
|
|
Рис. 4.1 |
Решение. Поскольку ax=0, ay=y, az=0, то
 .
.
Так как уравнение плоскости имеет вид y=2–x–z и нормаль к поверхности образует с осью Oy острый угол (это означает, что cosb>0 и поэтому перед интегралом нужно выбрать знак "+"), то
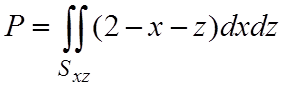 .
.
Далее, переходя к повторным интегралам, получим
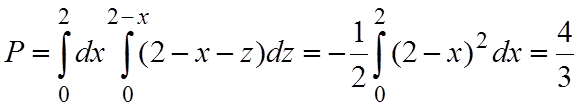 .
.
Пример 4.3. Вычислить поток векторного поля a=zk через внешнюю сторону сферы S: x2+y2+z2=1.
Решение. Поскольку ax=ay=0, az=z, то
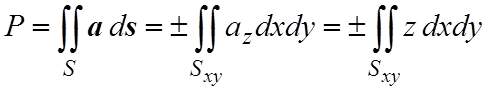 .
.
Здесь z нельзя выразить однозначной функцией от x и y для всей поверхности интегрирования. Разобьем поверхность на две части, верхнюю S' и нижнюю S'':
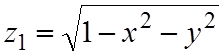 и
и
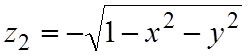 .
.
Тогда
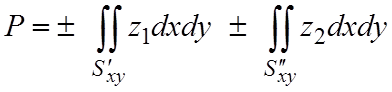 .
.
Перейдем к двойным интегралам. Так как S' – верхняя часть сферы, нормаль которой на всей полусфере образует с осью Oz острый угол, то
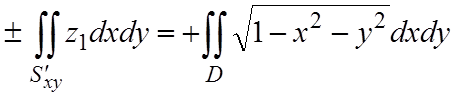 ,
,
где D – круг x2+y2£1. S'' – нижняя часть сферы, нормаль которой на всей полусфере образует с осью Oz тупой угол, то
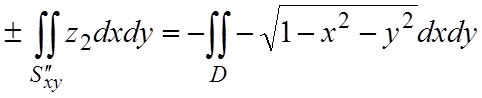 ,
,
где D – тот же круг. В результате получаем
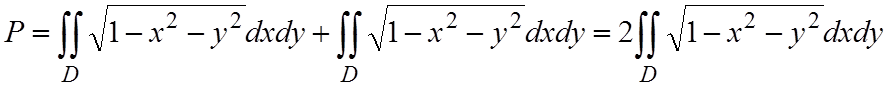 .
.
Перейдя в полярную систему координат, получим
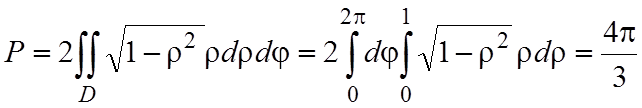 .
.
|
|
|
Рис. 4.2 |
Пример 4.4. Вычислить поток векторного поля a=2xi–yj через часть поверхности цилиндра S: x2+y2=R2, x³0, y³0, 0£z£H, в направлении внешней нормали (см. рис. 4.2).
Решение. Поскольку ax=2x, ay=–y, az=0, то
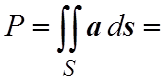
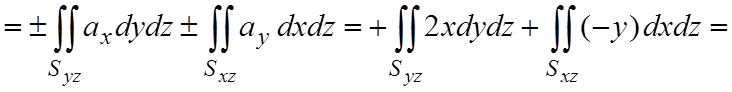
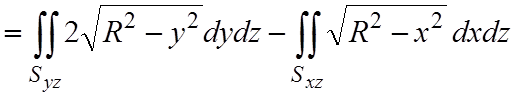 .
.
Поскольку Syz является прямоугольником размера R´H и Sxz – точно такой же прямоугольник, то оба интеграла в последнем выражении являются одинаковыми. Поэтому можно написать
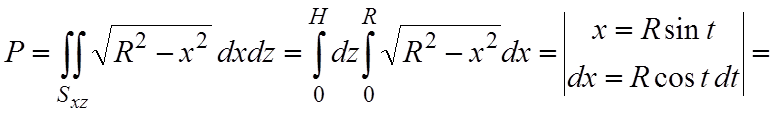
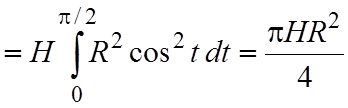 .
.
Особый интерес представляет случай, когда вычисляется поток через замкнутую поверхность. Обычно в таких случаях за положительную сторону поверхности принимают ее внешнюю поверхность. Поверхностный интеграл в этом случае обозначается следующим образом:
 .
.
Теорема Остроградского-Гаусса. Поток векторного поля a(r) через замкнутую поверхность S, находящуюся в этом поле, в направлении ее внешней нормали, равен тройному интегралу по области V, ограниченной этой поверхностью, от дивергенции этого векторного поля, т.е.
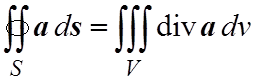 . (5.1)
. (5.1)
Здесь
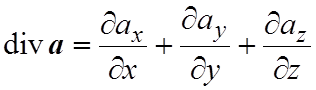 (5.2)
(5.2)
и называется дивергенцией векторного поля a.
Пример 5.1. Вычислить поток векторного поля
a=x3i+y3j+z3k
через сферу S: x2+y2+z2=R2.
Решение. Воспользовавшись формулой Остроградского-Гаусса, получим
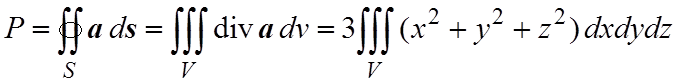 .
.
Откуда, вводя сферические координаты, получим
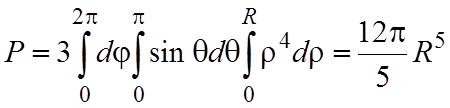 .
.
Пример 5.2. Вычислить поток векторного поля
a=x3i+y3j+R2zk
через
поверхность S: 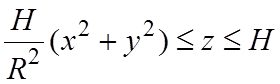 .
.
Решение. Поскольку diva=3(x2+y2)+R2, то формуле Остроградского-Гаусса получаем
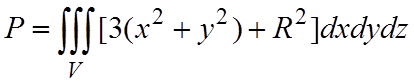
Перейдем к цилиндрическим координатам
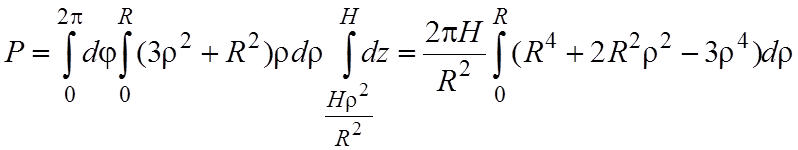
окончательно получаем
R = pHR4.
Особое значение в математике и ее приложениях играют криволинейные интегралы по замкнутой кривой (контуру). Такие интегралы называются циркуляциями и обозначаются
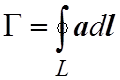 .
.
Теорема. Циркуляция дифференцируемого векторного поля aпо произвольному кусочно-гладкому замкнутому контуру L равна потоку вектора rota через поверхность S, ограниченную контуром L:
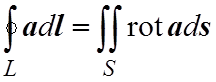 (5.3)
(5.3)
Здесь
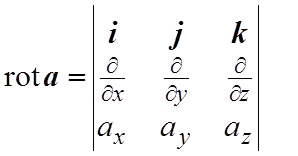 . (5.4)
. (5.4)
и называется ротором векторного поля a. Отметим, что единичный вектор n нормали к поверхности S направлен в такую сторону, чтобы обход контура L происходил в положительном, по отношению к n, направлении.
Пример 5.3. Вычислить ротор векторного поля a=x2y3i+j+zk в точке M(1;1;1).
Решение. Записываем

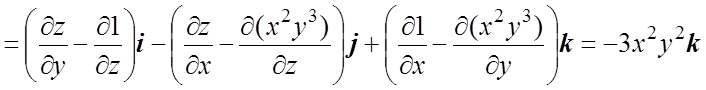 .
.
Таким образом,
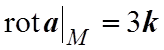 .
.
Пример 5.4. Вычислить циркуляцию векторного поля a=x2y3i+j+zk по окружности L: x2+y2=R2, z=0.
Решение. Поскольку rota=–3x2y2k, то по теореме Стокса получаем

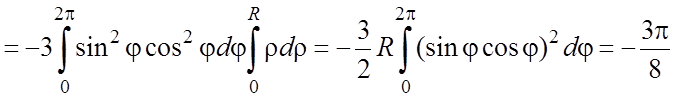 .
.
Такой же получится ответ, если
непосредственно вычислить криволинейный интеграл 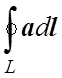 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.