Приближенное интегрирование дифференциальных уравнений, страница 3

Первое приближение. Для определения  y₁ по формуле (14) по необходимости придется ограничиться лишь двумя ее первыми членами. Тогда

.

Верхний индекс в скобках указывает на то, что эти величины получены в первом приближении. В результате получаем таблицу первого приближения.

k
0
1

Второе приближение. Имея , можем вычислить у₁ и у₂ по формулам (14) и (15), удержав в них по три члена. Тогда

              

              

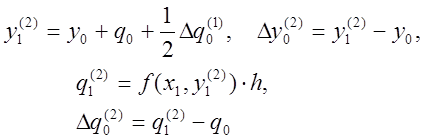
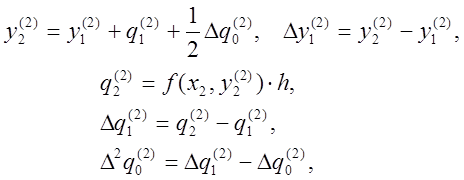
и таблица второго приближения принимает вид:

K
0
1
2

Второе приближение дает возможность воспользоваться полными формулами (14)-(15), которые позволяют перевычислить все имеющиеся в таблице значения. Однако полученная разность  иногда может оказаться столь малой, что перевычисление у₁ и у₂ не изменяет их значения.

После того, как значения у₁ и у₂ и соответствующие им разности перевычислены по полным формулам (14)-(15), для продолжения таблицы применяется основная формула (8).

Этот метод приближенного вычисления интеграла дифференциального уравнения (1), удовлетворяющего начальному условию (2), по формулам Адамса с составлением начала таблицы по способу А. Н. Крылова называют методом Адамса-Крылова.

О точности методов численного интегрирования дифференциальных уравнений. Контроль.

Оценка погрешности, допускаемой при применении методов численного интегрирования дифференциальных уравнений является весьма сложной задачей. В основе вывода формул Адамса (7)-(8) лежит идея приближенного интегрирования, основанного на интерполяции (линейной и квадратичной). В формуле (7) погрешность на одном шаге имеет порядок , а для формулы  (8) - . От шага к шагу неизбежно происходит накопление погрешности, что приводит к тому, что, например, для формулы (8) суммарная погрешность имеет уже порядок .

Очень важно при этом по возможности вычислить начало таблицы. Если при составлении начала таблицы будут использованы недостаточно точные методы, то последующее применение более точных формул уже не может исправить результата.

Практически необходимая точность обеспечивается соответствующим выбором шага. Для оценки правильности выбора шага может быть применен контрольный просчет с удвоенным шагом.

Вычисления с шагом h и 2h целесообразно проводить параллельно, чтобы возможно раньше заметить несовпадение результатов.

Заметим, что весьма важно обеспечить себя от появления случайных ошибок при выполнении вычислений. Для этой цели на каждом шаге проводятся контрольные вычисления с помощью какого-либо другого метода, имеющего такой же или более высокий порядок погрешности.

При вычислениях с помощью формулы (8), погрешность которой на каждом шаге порядка , в качестве контроля может быть применен метод Эйлера с уравниванием, имеющий погрешность такого же порядка. Для вывода контрольной формулы вспомним, что по рабочей формуле этого метода

               .

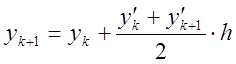Имея в виду, что , получим:

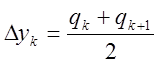.                (16)

Заметим, что величины , фигурирующие в правой части контрольной формулы (16), к моменту контроля уже вычислены и имеются в соответствующей колонке вспомогательной таблицы. Там же имеется и разность , которая и сравнивается с контрольным числом, получаемым по формуле (16).

Все вычисления по рабочим формулам (14), (15) и (8) ведутся с некоторым числом запасных знаков, чтобы не понизить порядок погрешности рабочей формулы за счет накопления погрешности вычислений.

Алгоритмы используемых методов