Після того як отримана деяка оцінка (наближене
значення ) ![]() параметра q, виникає питання: наскільки вона точ-на, тобто як
близько
параметра q, виникає питання: наскільки вона точ-на, тобто як
близько ![]() до q?
Таким чином, що випливає етапом для нас повинно бути побудова міри точності
цієї оцінки.
до q?
Таким чином, що випливає етапом для нас повинно бути побудова міри точності
цієї оцінки.
Будь-яка оцінка ![]() як
статистика вибірки є випадковою величиною, і, мабуть, її відхилення від
генерального параметра q також
буде випадковим. Отже, питання про оцінку цих відхилень носить вероятностный
характер, а саме: для довільного числа
як
статистика вибірки є випадковою величиною, і, мабуть, її відхилення від
генерального параметра q також
буде випадковим. Отже, питання про оцінку цих відхилень носить вероятностный
характер, а саме: для довільного числа ![]() можна
вказати лишь імовірність p, таку, що
можна
вказати лишь імовірність p, таку, що
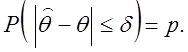
![]() (2.56)
(2.56)
Імовірність, що тут
фігурує, p називається довірчої (100p%) імовірністю, а ![]() інтервал
- довірчим (100p%) інтервалом, чи довірчою оцінкою.
інтервал
- довірчим (100p%) інтервалом, чи довірчою оцінкою.
Отже, будь-яка статистична оцінка є оцінка виду
![]() (2.57)
(2.57)
де ![]() і
і ![]() - деякі
випадкові числа. При побудові интервальных оцінок виду (2.57) використовуються
квантили випадкових величин.
- деякі
випадкові числа. При побудові интервальных оцінок виду (2.57) використовуються
квантили випадкових величин.
Квантилем кp розподілу випадкової величини ![]() з
функцією розподілу F(x) називається рішення рівняння
з
функцією розподілу F(x) називається рішення рівняння
F(kp) = p, (2.58)
т. е. квантиль кр є таке значення випадкової величини, що
![]() (2.59)
(2.59)
Деякі часто зустрічаються квантили носять спеціальні назви. Так,
квантили до0,1, до0,2, ..., до0,9
називають децилями, квантили до0,01, до0,02,
..., до0,99 - процентилями. Найбільш важливе значення має
квантиль ![]() , називаний медіаною розподілу.
, називаний медіаною розподілу.
Квантили стандартного нормального розподілу позначаються
через up. Їх легко знайти безпосередньо з таблиці додатка А.
Якщо ![]() те, підбираючи таке х, для якого
те, підбираючи таке х, для якого ![]() ми знайдемо, що
ми знайдемо, що ![]() Якщо ж
Якщо ж ![]() те підбирають таке х, для якого
те підбирають таке х, для якого ![]() і тоді up = x.
Наприклад, 40% квантиль u0,4=-0,25, 95% квантиль u0,95=1,64.
Для зручності користування деякі часто уживані квантили стандартного
нормального розподілу приводяться в таблиці додатка Б.
і тоді up = x.
Наприклад, 40% квантиль u0,4=-0,25, 95% квантиль u0,95=1,64.
Для зручності користування деякі часто уживані квантили стандартного
нормального розподілу приводяться в таблиці додатка Б.
Квантиль xp загального
нормального розподілу з параметрами a і ![]() виражається
через квантиль up стандартного розподілу по формулі (2.35)
виражається
через квантиль up стандартного розподілу по формулі (2.35)
![]()
Наприклад, 95% квантиль для нормального розподілу з параметрами а
= 4, ![]() дорівнює
дорівнює
x0,95 = 4 + 0,5·1,64 = 4,82.
Поняття квантиля використовується не тільки для нормального, а і для інших розподілів: Стьюдента, Пирсона, Фишера і т.д. Якщо відомі два квантиля кs і кq довільні розподіли, то, мабуть,
![]()
![]()
![]() (2.60)
(2.60)
Сформулюємо тепер зворотну задачу : по заданій
імовірності р визначити довірчий інтервал. Очевидно, у такій постановці
ця задача має незліченну безліч рішень - імовірності р відповідає будь-як
оцінка виду ![]() де
де ![]() Однак
якщо в якості квантилей вибрати симетричні відносно
Однак
якщо в якості квантилей вибрати симетричні відносно ![]() квантили
квантили
![]() і
і ![]() те
довірчий 100% інтервал
те
довірчий 100% інтервал
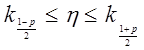 (2.61)
(2.61)
буде уже визначатися однозначно.
У додатках, у зв'язку з перевіркою різних статистичних
гіпотез (див. § 2.5), довірчу імовірність р
представляють у виді ![]() де
де ![]() -
рівень значимості. У даному випадку
-
рівень значимості. У даному випадку ![]() - імовірність події,
протилежного події (2.61). При заданому рівні значимості
- імовірність події,
протилежного події (2.61). При заданому рівні значимості ![]() з (2.61) одержуємо
з (2.61) одержуємо
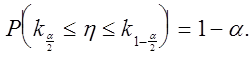 (2.62)
(2.62)
|
Малюнок 2.7 |
На мал. 2.7 представлений зв'язок між квантильны-ми границями ![]() ,
, ![]() і
довірчої вероятно-стью
і
довірчої вероятно-стью ![]() у випадку, якщо випадкова
величина
у випадку, якщо випадкова
величина ![]() має симетричний розподіл з нульовою
медіаною (наприклад, стан-дартное нормальне рас-пределение чи распреде-ление
Стьюдента).
має симетричний розподіл з нульовою
медіаною (наприклад, стан-дартное нормальне рас-пределение чи распреде-ление
Стьюдента).
Тому що ![]() те
те ![]()
![]() З умови симетрії видно,
що
З умови симетрії видно,
що ![]() Площа заштрихованої фігури дорівнює
довірчої імовірності
Площа заштрихованої фігури дорівнює
довірчої імовірності ![]()
Отже, у випадку симетричних розподілів (мал. 2.7)
100(1-![]() )% довірчий інтервал має вид
)% довірчий інтервал має вид
![]() (2.63)
(2.63)
Довірча
оцінка генерального параметра.Потрібно побудувати
довірчу оцінку генерального параметра q
(щирого результату спостережень, щирого значення деякого параметра,
математичного чекання досліджуваного розподілу). Нехай ![]() -
обрана за якоюсь методикою крапкова оцінка параметра q, і вона лінійно залежить від результатів спостережень
-
обрана за якоюсь методикою крапкова оцінка параметра q, і вона лінійно залежить від результатів спостережень
![]() Тоді випадкова величина
Тоді випадкова величина ![]() має той же тип розподілу, що і випадкові
величини
має той же тип розподілу, що і випадкові
величини ![]() Якщо з якихось розумінь уста-новлено, що
можна прийняти нормальний закон розподілу для
Якщо з якихось розумінь уста-новлено, що
можна прийняти нормальний закон розподілу для ![]() , те це
означає, що й оцінка
, те це
означає, що й оцінка ![]() задовольняє нормаль-ному закону
задовольняє нормаль-ному закону ![]() ~
~![]() НАДАЛІ це і припускаємо.
НАДАЛІ це і припускаємо.
Розглянемо основні задачі оцінювання невідомих параметрів, що виникають при обробці спостережень.
Задача 1
Оцінка параметра q при відомій дис-персии ![]() .Припустимо, що за
результатами попередніх спостережень дисперсія
.Припустимо, що за
результатами попередніх спостережень дисперсія ![]() відома.
Тоді, згідно (2.44), статистика
відома.
Тоді, згідно (2.44), статистика 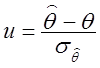 ~
~![]() і, з огляду на (2.63),
знаходимо
і, з огляду на (2.63),
знаходимо
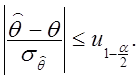
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.