Планирование и обработка результатов полного факторного эксперимента, страница 2

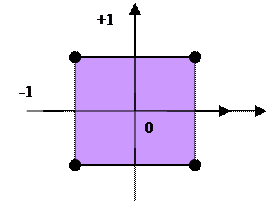
Для n= 2 число опытов m = 4 ипостроение плана можно наглядно показать на рис.2. Координаты вершин квадрата (1-4) соответствуют условиям  соответствующих опытов: (-1,1), (1,1), (-1,-1), (1,-1)

 

                                                X₂

                                    1                      2

	+1    X1

 

                                    3                      4

-1

                                     

                                       Рис.2. ПФЭ  для двух факторов.

При n= 3 число опытов  m = 8, условия опытов соответствуют координатам вершин куба, и матрица планирования имеет вид:

                  Таблица 1

№ опыта	X1	X2	X3	Y
1	-1	-1	-1	Y1
2	+1	-1	-1	Y2
3	-1	+1	-1	Y3
4	+1	+1	-1	Y4
5	-1	-1	+1	Y5
6	+1	-1	+1	Y6
7	-1	+1	+1	Y7
8	+1	+1	+1	Y8

Матрица  планирования ПФЭ для любого числа факторов обладает следующими свойствами:

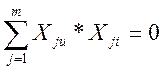1. ;            u ≠ i;   u, i = 1,2,…n;
2.  ;            j = 1,2,…n;

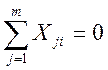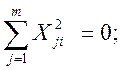3.            j = 1,2,…n;

Первое свойство – равенство нулю скалярных произведений двух любых векторов-столбцов – называется свойством ортогональности матрицы планирования. Второе свойство – равенство нулю суммы элементов любого вектора-столбца – называется свойством симметричности матрицы планирования.

План в кодированных факторах составляется на этапе подготовки эксперимента и на этапе обработки его результатов. Для выполнения эксперимента необходимо от кодированных факторов перейти к размерным:

                                                    Z_i =  Z_i⁰  +   ΔZ_i  *  X_i                                                (5)

Результаты измерений отклика во всех опытах составляют вектор наблюдений  (столбец Y табл.1).

          1.3. Регрессионный анализ результатов ПФЭ.

Регрессионный анализ результатов планированного эксперимента выполняется по аналогии с регрессионным анализом пассивного эксперимента, но за счёт свойств матрицы планирования существенно упрощается.  Первоначально зависимость отклика от факторов предполагается линейной

Ŷ   =  b₀ + b₁ X₁ + b₂ X₂ +… + b_n X_n                                             (6)

Например, для n=3:

                                      Ŷ   =  b₀ + b₁ X₁ + b₂ X₂  +  b₃ X₃                                          (7)

Коэффициенты регрессии b_i(линейные эффекты) определяются методом наименьших квадратов (см. лаб. работы №1 и №2).

 Благодаря свойству ортогональности  информационная матрица становится диагональной:

                         ,                                                              

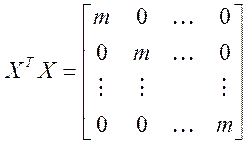  матрица, обратная информационной, также диагональная

                         ,

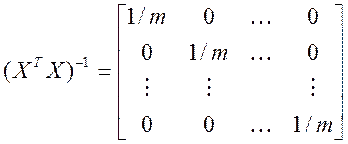 и коэффициенты регрессии рассчитываются по следующим формулам:

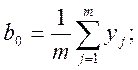
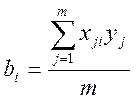                                  ,      i = 1,2..n                              (8)

где  - экспериментальное значение отклика в j-ом опыте.

Все коэффициенты в ортогональных планах имеют одинаковую погрешность, которая рассчитывается по формуле:

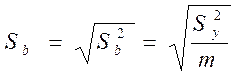                               ,                                                                (9)

где  - дисперсия коэффициента,   - дисперсия измерения отклика.

Для расчёта дисперсии измерения отклика выполняют несколько измерений отклика (L≥2) в каждом опыте или несколько параллельных опытов в центре плана. В первом случае число степеней свободы дисперсии измерения отклика:           

f = m·(L-1),    во втором случае -f = L-1.

Проверка значимости влияния факторов на отклик выполняется по критерию Стьюдента (см. лаб. работу №2). Расчётное значение t_i сравнивается с табличным t_таб(P,f). Если расчётное значение меньше табличного, i-й фактор незначим. Незначимые факторы исключаются из регрессии, их исключение не влечёт за собой изменения оставшихся коэффициентов.

Проверка адекватности осуществляется по критерию Фишера точно так же, как при обработке результатов пассивного эксперимента.

          Если линейная модель оказалась неадекватной, можно дополнить её произведениями факторов и получить неполную квадратичную модель: