Метод координат. Векторная алгебра. Скалярное умножение. Плоскость в пространстве. Прямая в пространстве, страница 2

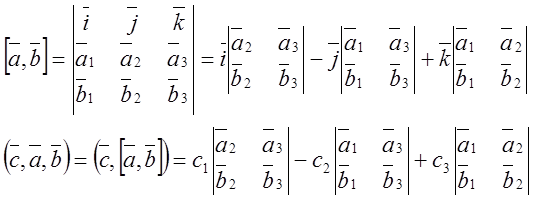
Таким образом: .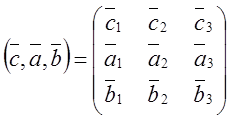

Несколько векторов называют компланарными, если они параллельны одной плоскости.

Критерий компланарности для 3-х векторов: компланарны если объём параллелепипеда, построенного на них, равенство нулю, т.е. .

Плоскость в пространстве.

Уравнение плоскости, заданной принадлежащей ей точкой M₀(x₀;y₀;z₀) параллельной двум векторам . Возьмём произвольную точку M(x;y;z) и пусть она принадлежит плоскости. Значит, вектора  и  компланарны. Условие компланарности в этом случае и есть уравнение:

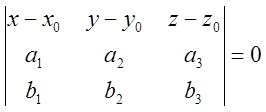
Уравнение плоскости, проходящей через 3 точки, не лежащие на одной прямой. Эта ситуация превращается в предыдущую если считать, что плоскость задаётся точкой M₁ и векторами . Поэтому уравнение:

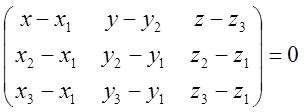
Прямая в пространстве.

Всякую прямую в пространстве можно рассматривать как линию пересечения 2-х плоскостей. Точки, принадлежащие двум поверхностям, должны удовлетворять обоим уравнениям этих поверхностей, или, что равносильно, системе этих уравнений.

Замечание. Наоборот, всяка такая система задаёт прямую, если только нормали не коллинеарны.

Уравнения рассмотренного типа и называют общими уравнениями прямой.

Канонические уравнения прямой.

Всякую прямую можно задать, зафиксировав точку M₀(x₀;y₀;z₀) на этой прямой и направляющий вектор , т.е. вектор, параллельный этой прямой. Произвольная точка пространства M с координатами (x;y;z) принадлежит рассмотренной прямой когда векторы  и  коллинеарны. Таким образом, уравнение:

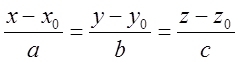, где наборы чисел x₀,y₀,z₀ – координаты некоторой точки на данной прямой, а числа a,b,c – координаты направляющего вектора.

Замечание. Некоторые (но не все) координаты направляющего вектора могут быть нулями. Поэтому, в канонических уравнениях допускаются некоторые нулевые знаменатели.

Взаимное расположение прямой и плоскости.

1. Прямая с направляющим вектором  и плоскость с нормалью  перпендикулярны когда эти векторы коллинеарны. Поэтому, условие:

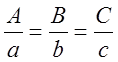, где прямая: 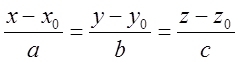, а плоскость: Ax+By+Cz+D=0.

2. Параллельность обеспечивает перпендикулярность указанных векторов: Aa+Bb+Cc=0.

В этом случае прямая может быть параллельна плоскости(Ax₀+By₀+Cz₀+D≠0), а может в ней содержаться(Ax₀+By₀+Cz₀+D=0).

Если же требуется обнаружить наличие общих точек, то следует рассмотреть систему, состоящую из уравнений прямой и плоскости. Её совместность (наличие у системы хотя бы одного решения) означает что общие точки есть.

Кривые 2-го порядка.

Кривой 2-го порядка называется всякая кривая, задаваемая уравнением вида

Ax²+Bxy+Cy²+Dx+Ey+F=0

Где хотя бы один из коэффициентов A, B, C отличен от нуля, т.е. |A|+|B|+|C|>0.

1. Окружность.

Это множество всех точек плоскости, равноудалённых от точки, называемой центром.

(x-a)2+(y-b)²=r²

a,b – координаты центра, r – радиус.

2. Эллипс.

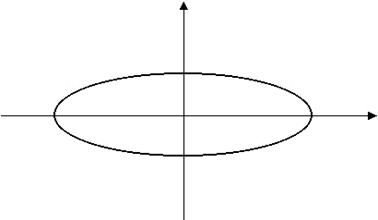Это множество всех точек плоскости, для каждой из которых сумма расстояний до двух фиксированных точек, называемых фокусами, больше чем между расстояние между фокусами.

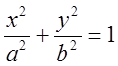
В этом случае фокусы эллипса лежат на одной из координатных осей симметрично относительно начала координат. А поэтому, и сам эллипс симметричен относительно обеих осей и относительно начала координат:

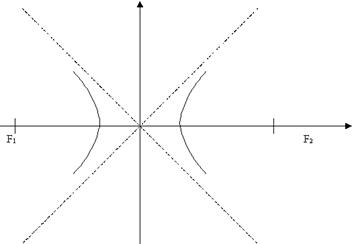3. Гипербола.

Это множество всех точек плоскости, для каждой из которых разность расстояний до двух фиксированных точек, называемых фокусами гиперболы, есть величина меньшая чем расстояние между фокусами.

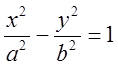
Такая гипербола имеет фокусы, лежащие на оси ОХ, симметричные относительно начала координат. Сама гипербола обладает такими же симметриями, как и эллипс.

4. Парабола.

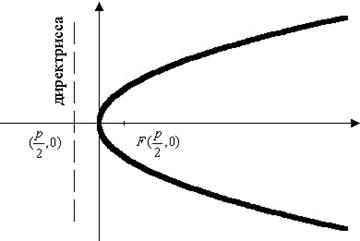Это множество всех точек плоскости, для каждой из которых расстояния до фиксированной точки (фокуса) и фиксированной прямой (директриссы) равны.

y²=2px, p>0

Пусть дано произвольное уравнение 2-го порядка. Оно задано относительно системы координат XY, выбранной заранее и. Требуется выбрать систему, в которой уравнение этой кривой сильно упростилось бы.

Две декартовы системы назовём одинаково ориентированными, если в обеих системах OY получается поворотом OX на 90^◦ в одну и ту же строну. Будем рассматривать системы с одинаковой единицей масштаба.

Любая такая система может быть получена из исходной системы с помощью параллельного переноса и поворота относительно начала координат.

Параллельный перенос.

Система  получена из (x,y).

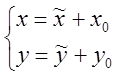
Поворот относительно начала координат.