Определение единиц измерения «Бит», «Бит/с», «Бод». Определение количества информации. Определение скорости модуляции и скорости передачи информации, страница 2

Исходные данные:

-  заданные информационные единичные элементы: «1111»;

-  вероятность ошибки Р₀ = 2 ·10^-2.

Решение.

1.  Исходя из требуемого кодового расстояния d₀ = 3 определим количество проверочных элементов r, равное показателю степени образующего полинома. В данном случае можно воспользоваться формулой 6.9 [1] r ³ log₂(n +1), т. е. 2^r ³ n +1. Так как число информационных элементов известно (k = 4) то, учитывая что n = k + r  имеем 2^r ³ k + r +1 = r + 5, отсюда r = 3. Следовательно, необходим код (n = 7; k = 4). По таблице 6.2 [1] при r = 3 находим образующий полином:  Р(х) = х³ + х² + 1. Дальнейшее решение производим в следующей последовательности:

1.1.  Представляем информационную часть кодовой комбинации в виде полинома ;

1.2.  Умножаем Q(х) на х³ (т. е. сдвигаем на  r = 3)

                          ;

1.3.  Делим на образующий полином Р(х)

                               

                                       

                        

                        

                           

                                

                                       

           Остаток от деления

1.4.  По формуле 6.19 [1] находим полином F(x), который представляет собой разрешенную кодовую комбинацию циклического кода

                    

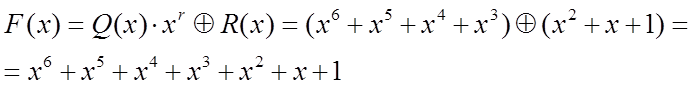
    Следовательно, искомая кодовая комбинация: «1111 111».

 

                                                                                         k      r

2.  Образующий полином представляет собой неприводимый многочлен, со степенью, равной количеству проверочных разрядов r. Образующий полином выбирается из таблицы неприводимых многочленов.

3.  Примитивными или неприводимыми полиномами являются многочлены, которые делятся без остатка только на самого себя или на единицу. Из теории высшей алгебры известно, что неприводимые полиномы образуются разложением на множители двучлена . Например, двучлен  можно разложить на три множителя , каждый из которых является неприводимым многочленом. Остатком от деления на примитивный полином степени r является полином, степень которого меньше r. Следовательно, примитивный полином степени r позволяет формировать ненулевых остатков.

4.  Проверяем правильность построения кодовой комбинации путем деления на выбранный образующий полином :

            

                                       

                       

                       

                               

                                      

                                               0  

   Остаток от деления равен , следовательно построенная кодовая комбинация циклического кода является разрешенной.

5.  Упрощенная структурная схема кодирующего устройства для выбранного кода приведена на рисунке 1.

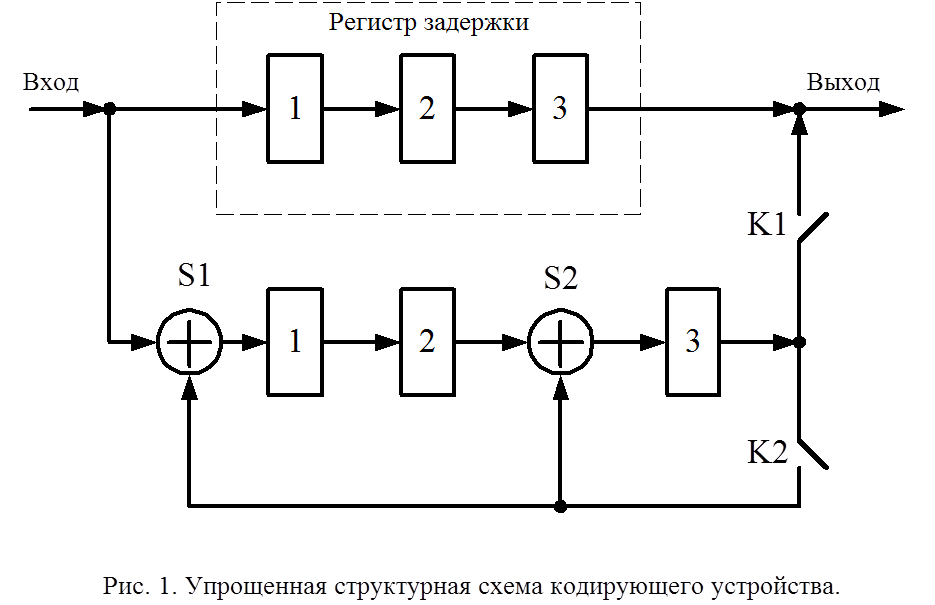
   Данная схема содержит регистр задержки, формирователь проверочной группы, включающий сдвигающий регистр и сумматоры по модулю 2 в цепи обратной связи, а также ключи K1 и K2, обеспечивающие необходимую последовательность функционирования. Число ячеек регистра задержки и регистра сдвига выбирается равным степени образующего полинома, а сумматоры по модулю 2 включаются перед ячейками, которые стоят на позиции единиц в образующем полиноме. Образующий полином равен , что соответствует «1101». Таким образом, регистр задержки и сдвигающий регистр содержат по три ячейки, а сумматоры по модулю 2 включены перед первой и третьей ячейками сдвигающего регистра.

6.  Для определения минимального количества ошибок, обнаруживаемых и исправляемых циклическим кодом с минимальным кодовым расстоянием d₀ = 3, воспользуемся соотношениями 6.5 – 6.6 [1].

6.1.  Для обнаружения всех ошибок кратности t₀ необходимо, чтобы соблюдалось неравенство:

                           – следовательно, заданный циклический код

          может обнаруживать все ошибки кратности не более t₀ = 2.

6.2.  Для обеспечения возможности исправления всех ошибок кратности t_и необходимо, чтобы соблюдалось неравенство:

                           – следовательно, заданный циклический код

          может исправлять все ошибки кратности не более t_и = 1.