Дифференциальные уравнения. Общие понятия, страница 2

                    - уравнение для первообразной - уравнение с разделяющимися переменными, решение которого:

                   

в) - уравнение не содержит независимую переменную в явном виде.

 Пусть , .

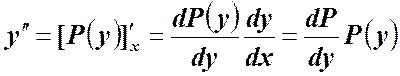В результате  имеем уравнение 1 порядка относительно неизвестной функции . Его решение

                    .

Так как , то

                   

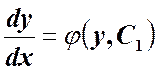
          или

                    -

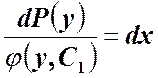уравнение для первообразной :

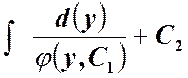=- общее решение или общий интеграл.

6. Линейные дифференциальные уравнения второго порядка без правой части(однородные). Линейным однородным уравнением второго порядка называется уравнение вида

                   

где  и - заданные функции.

Свойства линейных уравнений.

1.Если  является частным решением уравнения

  

   то и  также является решениями.

Известно, что  (-решение). Покажем что  -также решение. Подставим  в уравнение  или , что и требовалось доказать.

2. Если  и - частные решения уравнения, то

также является решением этого уравнения , удовлетворяют уравнению . Подставив  в уравнение

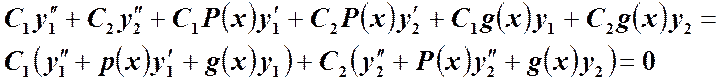
3. Функции  и  называются линейно-зависимыми на некотором множестве значении , если существуют такие числа  и , одновременно не равные нулю, что выполняется соотношение . Полагая, что 0, поделим равенство  и получим , 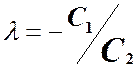- определение линейной зависимости функций.

Если таких постоянных ( или постоянной )  при выполнении условия  не существуют, то функции линейно независимы.

В уравнении . Функции - линейно зависимы, т.к. есть коэффициенты (1,1,-1) при которых выполняется условие 1. . Функции 1 и x линейно зависимые, т.к. очевидно, что нет такого числа , чтобы при произвольном x

                                        1= или

Точно также равенство  возможно только при

4. Определитель Вронского. Условие линейной зависимости.

Определителем Вронского  называют определитель вида:

                              ==.

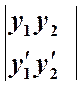Необходимым и достаточным условием линейной зависимости функции  и  является равенство нулю определителя Вронского.

          Необходимость. Дано: . Требуется доказать =0.

Подставив ,  в определитель , получим

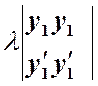                                        =0.

          Достаточность. Также очевидно: если =0, то стороны пропорциональны и           .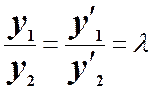

          Следствие. Неравенство нулю определителя Вронского достаточно для определения линейно независимых решений.

Действительно.  При  невозможно выполнение равенства , то есть, отсутствие линейной зависимости. Любая совокупность независимых решений  и  уравнения  называется фундаментальной системой.

          Таким образом, - фундаментальная система решений уравнения             .

5. Теорема об общем решении .

Если  и  образуют фундаментальную систему решений уравнения , то общее решение имеет вид:

                                        

По определению, решение, содержащее конечное число(2) произвольных постоянных, называется общим, если из него при определенных числовых значениях постоянных получается любое частное решение. Как следует из теоремы существования и единственности любое частное решение обозначено определяется начальными условиями: при   и , где - любые числа.

Мы докажем, что такое решение есть общее решение, если покажем, что в решении  постоянные  определены так, чтобы удовлетворялись начальные условия. Для определения  имеем систему уравнений:

                                        

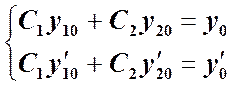
Определитель этой системы - определитель Вронского.

           так как  и  линейно  независимы и, следовательно, система имеет при данном значении  единственное решение, удовлетворяющее данным начальным условиям, что и требовалось доказать.