В данном методе применяется поэтапное исключение Гаусса (рис. 1). Известно, что если система линейных уравнений имеет ленточную матрицу коэффициентов и решается посредством гауссова исключения, причем главные элементы выбираются на главной диагонали, то вся арифметика ограничена лентой, вне которой никаких новых ненулевых элементов не возникает. Гауссово исключение можно проводить «на месте», поскольку для любого ненулевого элемента, если он появится, уже зарезервирована позиция в схеме хранения. [9]
Предположим, что на некотором этапе матрица коэффициентов А частично собрана, и пусть С — множество собранных конечных элементов (т. е. конечных элементов, элементные матрицы которых уже собраны). На данном этапе n узлов сетки могут быть разбиты на три множества: G — множество полностью собранных узлов, F — множество частично собранных узлов или фронт, Η — множество не собиравшихся узлов.
Ясно,
что если элемент е не входит в С, то 
= 0, если либо i, либо j, либо оба
принадлежат G. Это значит, что все строки и столбцы А, ассоциированные с узлами
из G, сейчас полностью собраны. Заметим еще, что 
= 0, если i
G, а jH, потому что Εi
∩ Ej = O. Вид частично собранной матрицы А на данном этапе показан на рис. 4.
Понятно, что все неизвестные, соответствующие узлам из G, можно исключить и заполнение будет происходить только в области, отмеченной надписью «частично собрано». Как только это сделано, собираются новые элементы из Ε — С, переопределяются множества G, F и Η и исключаются новые переменные. Фронт движется по сетке. Процесс продолжается, пока А не будет полностью собрана и разложена.
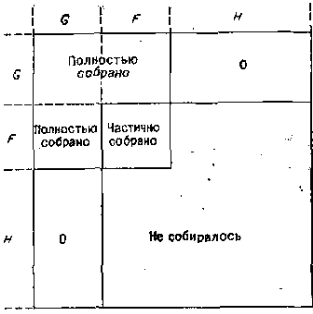
Рисунок 4 - Частично собранная матрица А
В практических реализациях фронтального метода исключения проводятся, как только они становятся возможными; порядок, в котором собираются элементы, берется такой, чтобы фронт оставался малым. Все узлы фронта лежат на границе между областью, покрытой элементами из множества С, и всеми прочими элементами.
К достоинствам метода можно отнести нечувствительность к ширине ленты СЛАУ, нечувствительность к нумерации узлов, не чувствительность к дискретизации области, а также то, что метод работает не только на положительно определенной матрице.
Сравним размерности используемых для решения матриц коэффициентов для фронтального метода и одного из ленточных методов решения СЛАУ.
Для этого рассмотрим прямоугольную область, разбитую на прямоугольные конечные элементы, число точек в высоту a, в ширину b (рис. 5). Предположим a меньше b и проведем нумерацию точек по меньшей стороне [4, 5], тогда ширина ленты СЛАУ будет (a+1)*6, а размерность самой матрицы a*b*6.
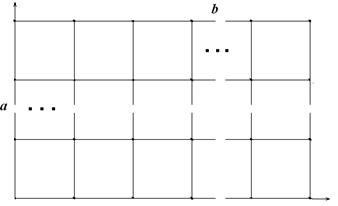
Рисунок 5 - Прямоугольная область с дискретизацией
Теперь оценим размерность матрицы коэффициентов при решении фронтальным методом. При нумерации элементов по меньшей стороне, получим на первом шаге размерность матрицы 4*6, после исключения Гаусса неиспользуемой более первой точки размерность будет 3*6 (рис. 6 б). На втором шаге размерность будет равняться 5*6, после исключения Гаусса – 4*6 (рис. 6 в). На шаге a, размерность будет составлять (a+2)*6, после исключения Гаусса a*6. На шаге a+1, размерность – (a+2)*6, после исключения (a+1)*6, на шаге а+2 – (a+2)*6. Отсюда видно, что максимальная размерность матрицы при решении фронтальным методом будет составлять (a+2)*6.
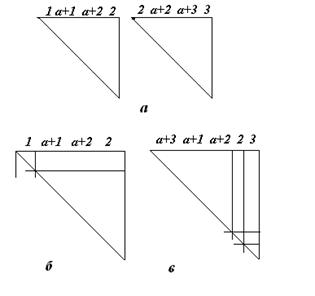
Рисунок 6 - Формирование матрицы коэффициентов фронтального метода для области на рис. 4: а) элементные матрицы коэффициентов жесткости для 1 и 2 го элементов, б) матрица коэффициентов и элемент для исключения Гаусса для первого элемента, в) для второго элемента
В случае более сложной геометрии области выгода от использования фронтального метода будет очевиднее – так как ширина ленты очень увеличивается, за счет больших разностей между номерами узлов на элементе. При этом фронт волны может быть малым.
Например, рассмотрим рис. 7. При дискретизации такой области возникнут проблемы, связанные с уменьшением ширины ленты матрицы коэффициентов за счет удачной нумерации точек. Фронт матрицы не превысит суммы количества точек находящихся на сторонах a и с.
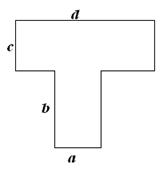
Рисунок 7 - Область сложной геометрии
В разработанном кафедрой математики и математического моделирования НФИ ГОУ ВПО «КемГУ» пакете программ «Композит-НК» в качестве решателей реализованы следующие методы: прямой метод разложения Холесского (рис. 2) и итерационный метод сопряженных градиентов (рис. 3 б).
Рассматривалась прямоугольная область, разбитая на треугольные симплекс-элементы. Для выявления пределов размерности возможной для расчета с помощью ПП «Композит-НК» прямым и итерационным методами проводилось сгущение расчетной сетки модели.
В результате выяснилось, что при расчете прямым методом
количество элементов составляет до 
, размерность СЛАУ до 
. При расчете
итерационным методом - количество элементов составляет до , размерность СЛАУ до 
.
Вывод Так как большинство расчетных областей конструкций имеют сложную шеометрическую форму, что приводит к большим размерностям СЛАУ и большой ширине ленты, требуется метод решения позволяющий сократить затраты машинной памяти при расчете напряженно-деформируемого состояния таких конструкций. Таким методом может быть фронтальный метод.
Литература:
1. Каледин В.О. Численно-аналитические модели в прочностных расчетах пространственных конструкций [Текст]/НФИ КемГУ. – Новокузнецк, 2000. -204 с.
2. Работнов Ю.Н. Механика деформируемого твердого тела. [Текст]/ Ю.Н. Работнов– М.: Наука. Гл. ред. физ.-мат. лит., 1988. – 712 с.
3. Тимошенко С.П., Гере Дж. Механика материалов: учебник для вузов. 2-е издание, стер. [Текст]/ С.П. Тимошенко - СПб.: Издательство "Лань", 2002. - 672с.
4. Зенкевич О. Метод конечных элементов в технике. [Текст]/ О. Зенкевич - М.: Мир, 1975. – 544 с.
5. Сегерлинд Л. Применение метода конечных элементов. [Текст]/ Л. Сегерлинд– М.: Мир, 1979. – 392 с.
6. Норри Д., Фриз Ж. де. Введение в метод конечных элементов. - [Текст]/ Д. Норри, Ж. де Фриз - М.: Мир, 1981. - 304 с., ил.
7. Вержбицкий, В.М. Основы численных методов: учебник для вузов/В.М. Вержбицкий. – М.: Высш. шк., 2002. -840 с.: ил.
8. Хейгеман Л., Янг Д. Прикладные итерационные методы [Текст]/ Л. Хейгеман, Д. Янг - М.: Мир, 1986. - 448с.
9. Писсанецки С. Технология разреженных матриц [Текст]/ С. Писсанецки– М.: Мир, 1988. - 410с, ил.
10. Irons B. M., A frontal solution program for finite element analysis [Текст]/ Internat. J. Numer. Methods Engrg., 2, No. 1, 5-32 (1970)
Резюме
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.