Линейные пространства. Определение и примеры. Геометрический изоморфизм линейных пространств

Каждый может привести лошадь к водопою, но никто не может заставить ее пить.

Линейные пространства

1. Определение

Что такое пространство? Математическое понимание пространства совсем другое, чем житейское.

   Линейное пространство – есть алгебра.

Что такое алгебра?

   Алгебра – это математическая структура, которая включает в себя некоторое множество-носитель, обозначим его , и на нем заданы операции. Их две: сложение и умножение на число.

Операция сложения, обозначается  (сумма  и ), удовлетворяет следующим свойствам:

1.  – симметрия (коммутативность),
2.  – ассоциативность,
3. должен быть особый элемент (зачеркнутый кружок), такой что .  называется нейтральным по сложению.
4. всякому  сопоставляется элемент , такой что .  называется противоположным.

По операции сложения  является абелевой группой (свойства 2-4 говорят, что это группа, а первое – что абелева).

Замечание:  замкнуто относительно операции + (сумма определена для любых элементов из  и всегда является элементом множества ). – бинарная операция.

       Операция умножения, обозначается . На самом деле их много, т. к. умножение на 0 – это одна операция, на 1 –другая, поэтому говорят, что в  определен оператор умножения на числа, удовлетворяющий свойствам:

5.  ,

6.  .

7.  ,

8.  .

Замечание:  замкнуто относительно операции ,  – унарная операция.

Элементарные теоремы:

1.  .

2.  Противоположный элемент  существует и единственен.

3.  .

4.  .

5.  Нейтральный по сложению  существует и единственен.

   Элементы пространства будем называть векторами или точками.

Мы говорим об абстрактном пространстве, т. е.  мы никак не определяли, а теперь рассмотрим конкретные линейные пространства.

2.  Примеры

·  Арифметические ЛП – .

Элементы  это упорядоченные наборы чисел 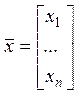 (будем записывать их столбцами, мы так хотим).

Чтобы  было пространством надо задать на нем + и  на число. Заведем еще .

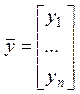Сложение определим следующим образом: 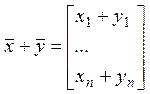 (покоординатное сложение).

Очевидно, что свойства 1, 2 выполнены.

Свойство3: в качестве нейтрального по сложению возьмем .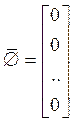

Свойство 4: .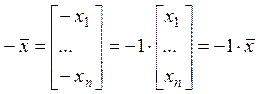

Все свойства выполняются, поэтому такое сложение годится.

       Умножение на число определим как покоординатное умножение на это число, а именно, 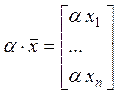, тогда все 4 свойства выполнены, а, следовательно, перед нами алгебраическая структура, которая является линейной.

Частный случай –  – множество чисел.

   Линейное подпространство. Может случиться, что в  содержится , которое само является линейным пространство. Такое множество  называется подпространством.

Упражнение. Доказать, что векторы вида 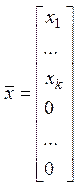образуют линейное подпространство в .

Как выглядит ? Пока никак.

·  Пространство свободных векторов .

Его элементы – направленные отрезки.

Если на экзамене при вопросе: «Что такое вектор?» вы скажете – «Направленный отрезок», то за такой ответ будет ставиться 2. Все зависит от того, в каком пространстве находимся.

Сложение определим следующим образом:

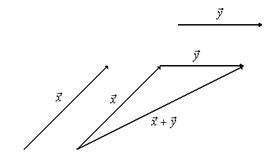
Где находятся эти отрезки? Нигде, они ни к чему не привязаны.

Два элемента равны, если  и имеют одно направление

Проверим выполнение свойств.

Свойство 1 выполняется по правилу параллелограмма:

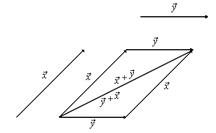
Свойство 2:

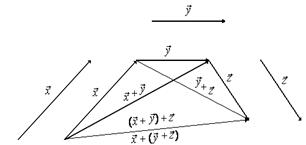
Свойство 3: Нуль-вектор . Длина равна 0, направлен безразлично куда.

       Умножение на число: , направлен в том же направлении, длина в  раз больше.

Свойство 5:

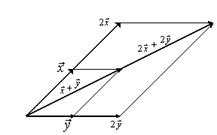
выполняется в силу геометрического подобия.

·  Геометрическое линейное пространство  (пространство радиус-векторов).

Его элементы .

В этом пространстве имеется выделенная точка .

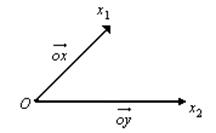При желании, то что вектор показывает носом можно обозначить ,  (тогда аналог нашему пространству).

·  Линейное пространство функций .

Элементы пространства – функции , ( – название функции).

Определим сложение:

т. е. в каждой точке к значению  прибавляем значение :

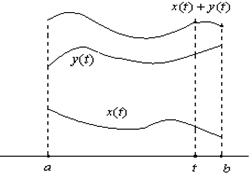
Так определяется сумма. Свойства 1, 2 выполнены в силу того, что в любой точке складываются числа.

Нейтральный по сложению:  - функция – константа (если const=0, то функция называется аннулятором).

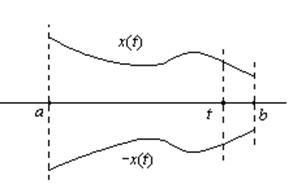
Противоположный элемент:

Умножение на число:

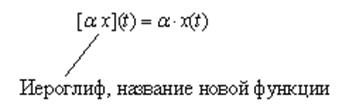
Следовательно, перед нами еще одно линейное пространство, хотя оно сильно не похоже на пространство, в котором мы живем.

Упражнение. Доказать, что все непрерывные функции являются подпространством , обозначается .

Дифференцируемые функции  также являются подпространством , кроме того, и , т. к. чтобы функция была дифференцируемой, она должна быть непрерывной. И т. д.:

-регулярные функции.

Упражнение. Доказать, что все функции, равные нулю в некоторой точке :  – являются линейным пространством.

3.  Геометрический изоморфизм линейных пространств

       Пусть имеется некоторое линейное пространство  (абстрактное) и мы хотели бы сделать его «видимым», «наглядным».

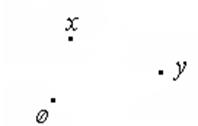
Для этого надо «рассадить» элементы по точкам пространства. Где-то сел бы нулевой элемент  из пространства , где-то сели бы элементы ,  и т. д.

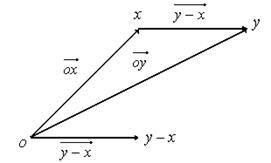Но тогда мы можем организовать стрелки ,  – отличие от нуля , ( – начало стрелки,  – конец стрелки).

Аналогично можно организовать стрелку  – отличие элемента  от , но  это точка из , следовательно, ей тоже соответствует точка пространства. Где она находится? Откладываем стрелку от .

Тогда  – правило из геометрического пространства ,

 – правило из , (именно поэтому вектора складываем по правилу параллелограмма, а не потому, что так сказал какой-то дядя).

Пример. Как в школе изображали ? Брали линейку, проводили одну ось , перпендикулярно к ней проводили другую ось –  и говорили, что задана ДСК. Почему именно так?

Выберем на плоскости точку 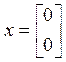, проведем ось . Что это значит? Это значит, выберем масштаб , тогда 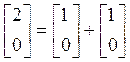 и т. д.

Появилась ось :

Аналогично строим ось . Выберем масштаб .

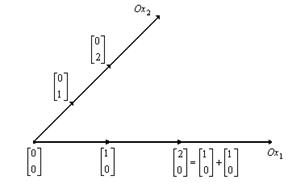
Вторая ось не обязательно перпендикулярна первой, это зависит от того, как выберем расположение точки .

Любую точку из  можем изобразить на построенной плоскости, причем однозначно: .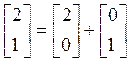

Следовательно, изоморфизм , геометрия возникает только здесь, не раньше.

4.  Пример линейного пространства

Пусть имеется набор элементов, обозначим его , которые мы умеем складывать и умножать на числа.

Рассмотрим элемент = ( – новый элемент,  - числа)  ().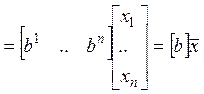

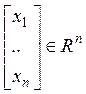Такой элемент  называется линейной комбинацией элементов .

Все линейные комбинации, заданные в системе векторов  являются линейным пространством. Это линейное пространство обозначается  и называется линейной оболочкой системы .

Упражнение. Убедитесь, что это линейное пространство.

Пример. Плоскость – это линейная оболочка двух непараллельных векторов:

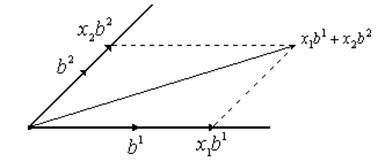Задавая , точки будут пробегать всю плоскость.

Линейная оболочка одного элемента  – это направление.

Пример.

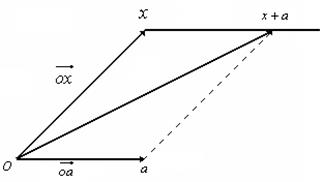Пусть  – уравнение в линейном пространстве .

Меняя значение параметра , получим геометрический образ прямой линии в геометрическом пространстве :

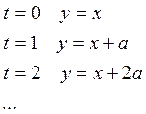
Например,  – прямая линия в пространстве функций . Такие прямые называются гомотопией.

 – геометрическая прямая. (Ильин, Позняк Аналитическая геометрия)

 – плоскость.