8. СТАТИСТИЧЕСКИЕ АСПЕКТЫ ИМИТАЦИОННОГО МОДЕЛИРОВАНИЯ
8.1. СТОХАСТИЧЕСКИЕ СИСТЕМЫ И ПРОЦЕССЫ
В общем случае исследуемая система может содержать элементы, свойства которых и поведение имеют некоторую неопределенность (случайность). Исследование таких (стохастических) объектов основывается на теории вероятности и математической статистики.
Стохастическим процессом называется упорядоченный временной набор случайных чисел.
Реализацией стохастического процесса является набор выборочных участков - временных рядов. Каждый прогон имитационной модели дает временные ряды изучаемых стохастических процессов.
Стохастический процесс называется стационарным, если закон поведения (распределение) случайных величин (СВ) любой его реализации не зависит от времени.
Эргодическим называется процесс, свойства которого могут быть оценены по результатам одного временного ряда.
Эксперимент.
Эксперимент ![]() является процедурой или процессом,
который можно наблюдать, но результат которого нельзя точно предсказать ( в
противном случае эксперимент не нужен). Множество всех полученных результатов
одного и того же повторяемого стохастического эксперимента называется
пространством
является процедурой или процессом,
который можно наблюдать, но результат которого нельзя точно предсказать ( в
противном случае эксперимент не нужен). Множество всех полученных результатов
одного и того же повторяемого стохастического эксперимента называется
пространством ![]() выборок. Обработка
результатов может дать новые знания (новый результат).
выборок. Обработка
результатов может дать новые знания (новый результат). ![]() может быть дискретным (конечным) или
непрерывным.
может быть дискретным (конечным) или
непрерывным.
8.2. ВЕРОЯТНОСТЬ
Вероятность является мерой возможности. Формальной мерой вероятности
является функция ![]() , которая удовлетворяет
следующим аксиомам:
, которая удовлетворяет
следующим аксиомам:
1. 0 £ ![]() (
(![]() ) £ 1 для любого
) £ 1 для любого ![]() (например бросание монеты).
(например бросание монеты).
2. ![]() (
(![]() ) = 1 для достоверного пространства
) = 1 для достоверного пространства ![]() (орел, решка).
(орел, решка).
3. ![]() (
(![]() È
È![]() È
È![]() È…) =
È…) = ![]() (
(![]() )
+
)
+![]() (
(![]() )+
)+
![]() (
(![]() )
+… для взаимоисключающих
)
+… для взаимоисключающих
экспериментов ![]() ,
, ![]() ,
, ![]() ,… (
,… (![]() (орелÈрешка) =
(орелÈрешка) = ![]() (орел) +
(орел) +![]() (решка)).
(решка)).
Вычисление вероятности основывается на законах теории вероятности, теории множеств, комбинаторном анализе.
Вероятностные характеристики СВ. Каждая СВ характеризуется вероятностью появления. Закон поведения (распределение) СВ также может быть вероятностным.
Вероятностное
распределение представляет собой некоторое правило задания вероятности для
каждого из всех возможных значений случайной переменной ![]() .
Правило задания вероятности имеет две формы в зависимости от того, является СВ
дискретной или непрерывной. Дискретная СВ (ДСВ) принадлежит конечному множеству
значений, непрерывная СВ (НСВ) - континууму значений.
.
Правило задания вероятности имеет две формы в зависимости от того, является СВ
дискретной или непрерывной. Дискретная СВ (ДСВ) принадлежит конечному множеству
значений, непрерывная СВ (НСВ) - континууму значений.
Для
дискретной СВ вероятность каждого ее значения ![]() Î
Î![]() задается функцией вероятности
задается функцией вероятности ![]() (
(![]() ),
принимающей для
),
принимающей для ![]() =
=![]() значение
значение
![]() (
(![]() ) =
) = ![]() (
(![]() =
=![]() ),
где 0 £
),
где 0 £ ![]() (
(![]() ) £ 1,
) £ 1, ![]() (
(![]() )
= 1.
)
= 1.
Альтернативой функции вероятности является функция распределения ![]() (
(![]() ):
):
![]() (
(![]() ) =
) = ![]() (
(![]() £
£![]() ),
),
что означает
вероятность того, что ![]() примет значение не больше,
чем
примет значение не больше,
чем ![]() . Свойства
. Свойства ![]() (
(![]() ):
):
1)
0 £ ![]() (
(![]() ) £ 1; 2)
) £ 1; 2) ![]() (-¥) = 0; 3.
(-¥) = 0; 3. ![]() (+¥) = 1.
(+¥) = 1.
Функции ![]() (
(![]() )
и
)
и ![]() (
(![]() )
связаны между собой:
)
связаны между собой:
![]() (
(![]() ) =
) = 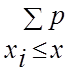 (
(![]() ) .
) .
Для непрерывных СВ вероятность ![]() (
(![]() ) = 0. Поэтому для них введено
понятие функции плотности вероятности
) = 0. Поэтому для них введено
понятие функции плотности вероятности ![]() (
(![]() ). Функция
). Функция ![]() (
(![]() ) должна удовлетворять условиям:
) должна удовлетворять условиям:
1) ![]() (
(![]() ) ³ 0; 2)
) ³ 0; 2) ![]() (
(![]() )
)![]()
![]() =
1.
=
1.
Функции ![]() (
(![]() ),
),
![]() (
(![]() )
и
)
и ![]() (
(![]() )
связаны друг с другом:
)
связаны друг с другом:
1)
![]() (
(![]() £
£![]() £
£![]() ) =
) = ![]() (
(![]() )
)![]()
![]() ; 2)
; 2) ![]() (
(![]() ) =
) = 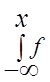 (
(![]() )
)![]()
![]() =
= ![]() (
(![]() £
£![]() ).
).
Первое выражение определяет вероятность того, что на интервале ![]() СВ примет значение из этого
интервала. Последнее выражение дает функцию распределения для непрерывной СВ.
СВ примет значение из этого
интервала. Последнее выражение дает функцию распределения для непрерывной СВ.
Математическое ожидание и моменты. Математическим ожиданием (МО) СВ является значение, равное
![]() [
[![]() ]
=
]
= 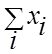
![]() (
(![]() ) для ДСВ;
) для ДСВ;
![]() [
[![]() ]
=
]
= ![]()
![]() (
(![]() )
)![]()
![]() для НСВ.
для НСВ.
Таким образом, математическим ожиданием является взвешенная по
вероятности средняя величина всех возможных значений ![]() ;
;
![]() -м моментом называется значение
-м моментом называется значение ![]() [
[![]() ],
равное
],
равное
![]() [
[![]() ]
=
]
= 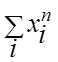
![]() (
(![]() ) для ДСВ;
) для ДСВ;
![]() [
[![]() ]
=
]
= 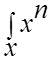
![]() (
(![]() )
)![]()
![]() для НСВ.
для НСВ.
МО есть ![]() [
[![]() ]
при
]
при ![]() = 1 и называется первым моментом.
= 1 и называется первым моментом.
Вариацией
![]() -го момента называется
-го момента называется ![]() -й момент среднего:
-й момент среднего:
![]() .
.
Особое значение в теории вероятности имеет второй момент среднего, называемый дисперсией:
![]() =
= ![]() .
.
Ковариацией случайных величин ![]() и
и
![]() называется величина
называется величина
![]() .
.
С ковариацией ![]() связан
коэффициент корреляции
связан
коэффициент корреляции
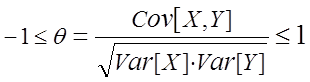 .
.
При ![]() > 0 с ростом
> 0 с ростом ![]() растет и
растет и ![]() .
При
.
При ![]() < 0 увеличение
< 0 увеличение ![]() приводит к падению
приводит к падению![]() . Если
. Если ![]() и
и
![]() независимы, то график
независимы, то график ![]() (
(![]() )
представляет собой набор случайных точек.
)
представляет собой набор случайных точек.
Функции случайных величин. Функция СВ также является СВ. Примеры:
1.
![]() ;
;
2.
![]() , где
, где ![]() - константа;
- константа;
3.
![]() ;
;
4.
![]() ;
;
5.
![]() ;
;
6.
![]() ;
;
7.
![]() .
.
Для независимых![]() ,
,![]()
![]() .
.
Выборочное среднее. В математической
статистике важную роль играет СВ, называемая выборочным средним (средним по
выборке) ![]() , где I - размер выборки из
вероятностного распределения:
, где I - размер выборки из
вероятностного распределения:
![]() =
= ![]()
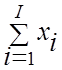 , где
, где ![]() -
одно или среднее из
-
одно или среднее из ![]() .
.
Если (I,![]() ) =
) =![]() , то
, то ![]() -
функция выборки со среднеквадратичным отклонением
-
функция выборки со среднеквадратичным отклонением
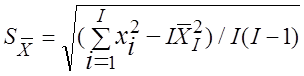 .
.
Если ![]() независимы и одинаково
распределены (НОР), то
независимы и одинаково
распределены (НОР), то
![]()
![]() =
= 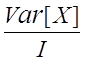 .
.
Это значит, что выбрав I достаточно большим, можно уменьшить дисперсию среднего до любой малой величины.
Законы
больших чисел. Поведение ![]() при увеличении
размера выборки определяется двумя теоремами.
при увеличении
размера выборки определяется двумя теоремами.
1. По мере роста ![]() величина
величина
![]() стремится к
стремится к ![]() с вероятностью, равной 1 - сильный
закон больших чисел. С ним связан слабый закон больших чисел:
с вероятностью, равной 1 - сильный
закон больших чисел. С ним связан слабый закон больших чисел:
![]()
![]() =
0 для любого
=
0 для любого ![]() 0,
0, ![]() ,
т.е. для любого положительного сколь угодно малого
,
т.е. для любого положительного сколь угодно малого ![]() вероятность
того, что модуль разности
вероятность
того, что модуль разности ![]() и
и
![]() превысит
превысит ![]() , стремится к нулю при
, стремится к нулю при ![]() .
.
2. При
определенных благоприятных условиях распределение суммы (не множества) ![]() независимых наблюдений СВ
независимых наблюдений СВ ![]() стремится к нормальному, когда
стремится к нормальному, когда ![]() , независимо от характера
распределения самой СВ
, независимо от характера
распределения самой СВ ![]() -
центральная предельная теорема.
-
центральная предельная теорема.
8.3. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ
|
1.
|
|
|
|
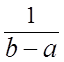 ;
;
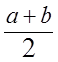 ;
;
|
|
|
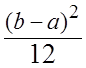 =
=
2. Треугольный (рис.8.2):
|
 |
|||||
|
|||||
|
|
|
|
|||
|
|
|
|
![]() =
= 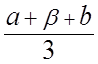 ;
;
![]() =
= 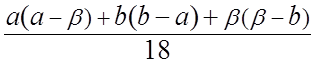 .
.
 |
|
|
![]()

![]() =
=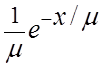 ;
;
![]() >
0;
>
0;
![]() =
= ![]() .
.
Если вероятность
того, что один и только один результат наступит на интервале ![]()
![]() пропорциональна
пропорциональна
![]()
![]() и
если наступление результата не зависит от наступления других результатов, то
величины интервалов между результатами распределены экспоненциально. Данный тип
процесса не оставляет последействия, что характеризует его марковские
свойства.
и
если наступление результата не зависит от наступления других результатов, то
величины интервалов между результатами распределены экспоненциально. Данный тип
процесса не оставляет последействия, что характеризует его марковские
свойства.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.