Построение базисных функций: Учебное пособие, страница 2

с глобальными узлами n = 1...4

Теперь мы получили более точное непрерывное параметрическое описание распределения потенциала u(x), но для того чтобы определить зависимость u(x), необходимо установить взаимосвязь между параметрами x и x для каждого элемента. Для этого удобно определить x как интерполяцию узловых значений.

Например, на первом элементе:

,                                                              (9)

Аналогичные зависимости будут справедливы и для остальных элементов.

Тогда зависимость потенциала от x, u(x), определяется следующими параметрическими выражениями:

,

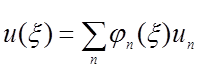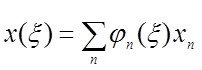.                                                                                                    (10)

Зависимость x(x) устанавливает связь между математическим пространством x (0 £ x £ 1) и физическим пространством x в диапазоне x₁ £ x £  x₂, как показано на рис. 7.

Рис. 7 демонстрирует, каким образом x и u соотносятся друг с другом посредством нормированной координаты . Значения x(x) и u(x) определяются из линейных интерполяций узловых переменных, а затем определяется зависимость u(x).

Квадратичные базисные функции

Особым свойством базисных функций, определенных выше, является то, что базисные функции, соответствующие конкретным узлам, принимают значения, равные 1 в данном узле, и равны нулю в остальных узлах элемента.

Этим обеспечивается независимость базисных функций. Это также является ключом к формированию базисных функций для интерполяций высших порядков.

Например, квадратичная зависимость u вдоль элемента требует наличия трех узловых параметров u₁, u₂ и u₃:

.                                                                      (11)

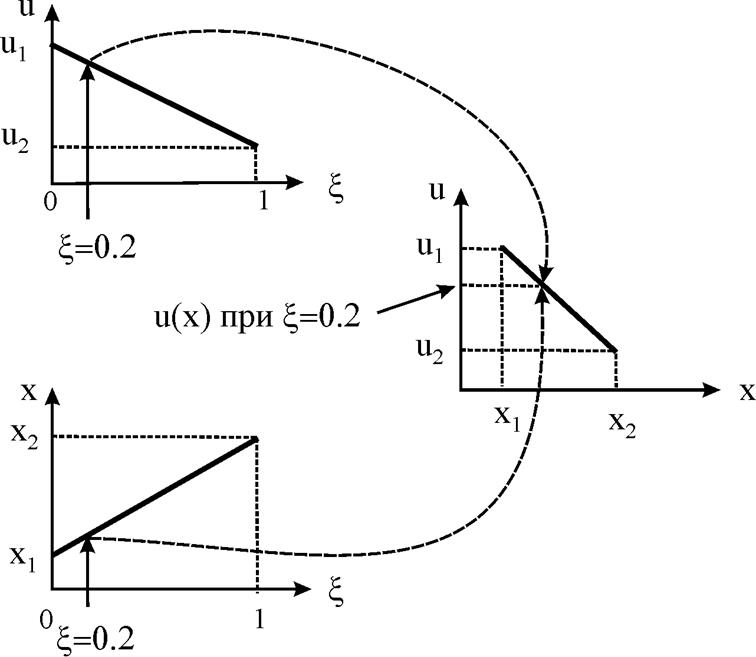
Рис. 7. Взаимосвязь между параметрами x и u

Квадратичные базисные функции показаны на рис. 8,

где

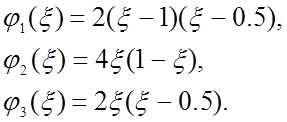
Двумерные и трехмерные элементы

Двумерные базисные функции формируются на основе описанных выше одномерных линейных функций.

Пусть

,

где

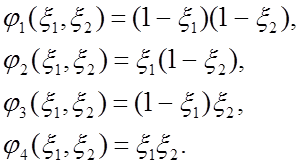                                                                                                    (12)

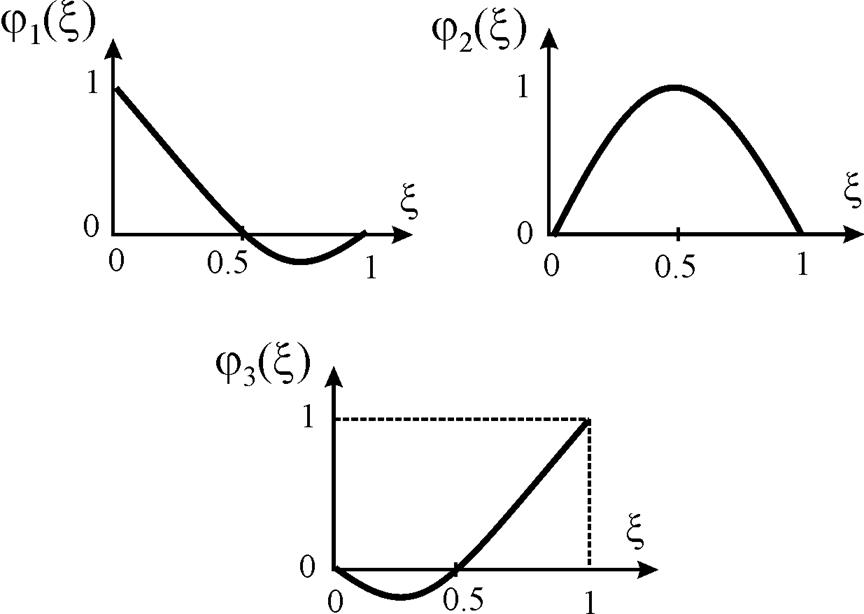
Рис. 1.8. Одномерные квадратичные базисные функции

Необходимо отметить, что при этом

,

где j₁(x₁) иj₁(x₂) – одномерные линейные базисные функции.

Аналогично

 и т.д.

Четыре базисные функции, описываемые выражениями (12), изображены на рис. 9.

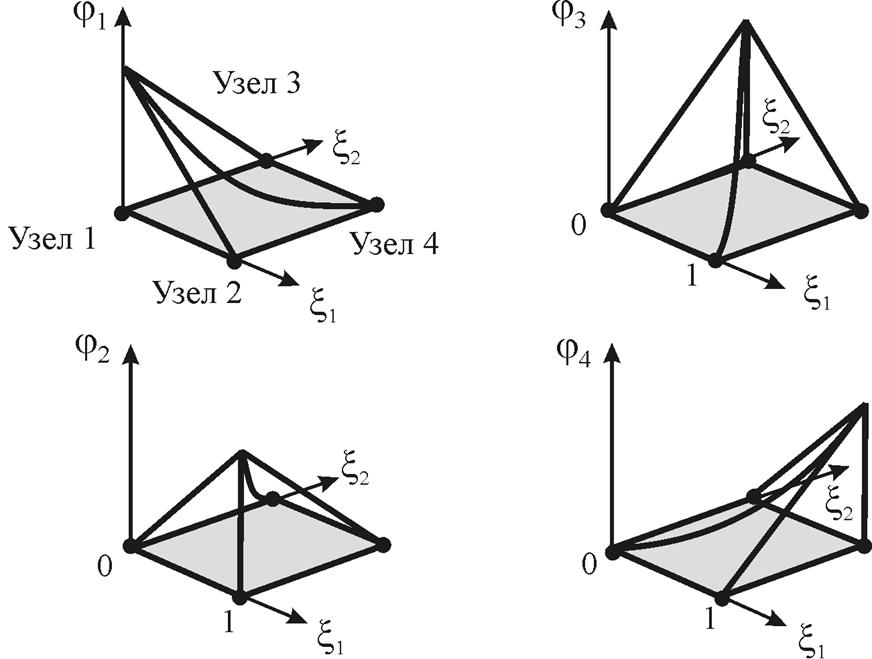
Рис. 9. Двумерные билинейные базисные функции

Заметим, что j_n(x₁,x₂)=1 в узле n и равно нулю в остальных трех узлах.

В результате потенциал u(x₁,x₂) получает вклад от каждого узлового параметра u_n, зависящего, в свою очередь, от j_n(x₁,x₂). Когда значение потенциала u(x₁,x₂) определяется в узле n, потенциал принимает значение u_n.

Геометрия элемента определяется по отношению к положению узла (x_n, y_n), при  n = 1, 2, 3, 4

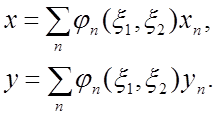                                                                                                    (13)

Выражения (13) обеспечивают соответствие между математическим пространством (x₁, x₂) и физическим пространством (x,y), где 0 £ x₁ £ 1;  0 £ x₂ £ 1.

Двумерные базисные функции высших порядков могут быть сформированы аналогичным образом из одномерных базисных функций.

К примеру, квадратично-линейный элемент (квадратичный по x₁  и линейный по x₂), состоящий из шести узлов (шеститочечный элемент), будет иметь следующий вид:

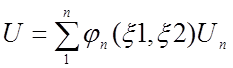,                                                                                                    (14)

где

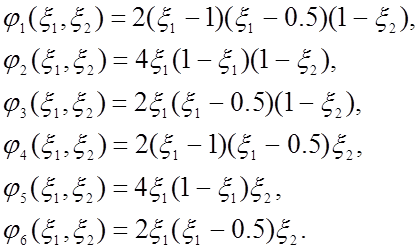                                                                                                    (15)

                                                                                                          

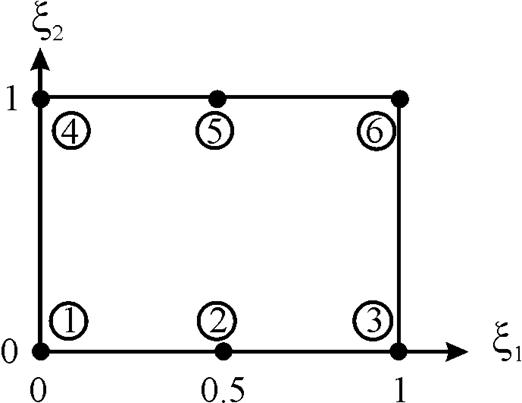
Рис. 10. Шеститочечный квадратично-линейный элемент

(номер узла в кружочке)

Трехмерные базисные функции формируются аналогичным образом и имеют восемь узлов (рис. 11), и описываются следующими выражениями:

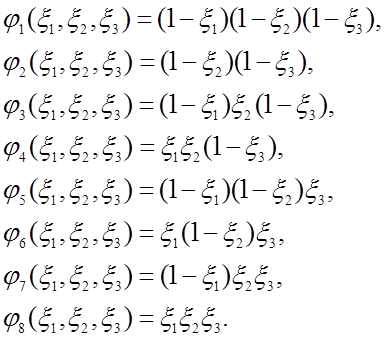                                                                                                    (16)

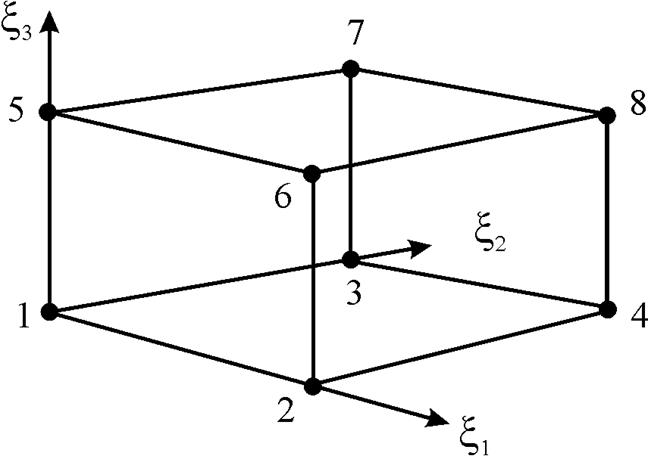
Рис. 11. Трехмерный восьмиточечный трилинейный элемент

Структуры высших порядков

Все рассмотренные выше базисные функции являлись базисными функциями Лагранжа, которые обеспечивают непрерывность параметра u на границах элементов. Часто возникает необходимость использовать базисные функции, которые также сохраняют непрерывность и производной от u по x на границах элементов. Проще всего это обеспечивается путем добавления дополнительных узловых параметров .

Эти базисные функции выбираются таким образом, что:

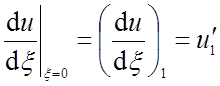   и 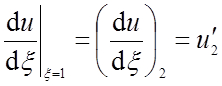  .                                                                                                    (17)

Поскольку u_n  одновременно относится к  двум смежным элементам, то непрерывность производной выполняется автоматически. Так как число элементов равно четырем,  то базисные функции должны быть пропорциональны . В этом случае они представляют собой кубические функции Эрмита:

,                                                                                                    (18)

тогда производная будет определяться выражением:

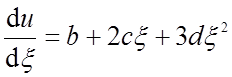.                                                                                                    (19)

Наложим следующие ограничения:

,

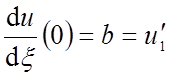,                                                                                                    (20)

.

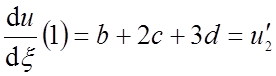Решим уравнения (20) относительно четырех неизвестных: a ,b ,c, d:

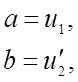
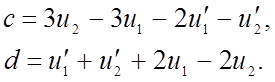                                                                                                    (21)

Подставим выражения (21) в уравнение (18):

                                                                                                    (22)

Перепишем выражение (22) в виде:

,                                                                                                    (23)

где

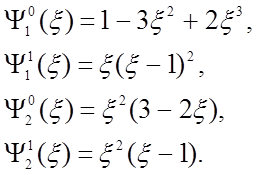                                                                                                    (24)

Функции (24) есть одномерные кубические базисные функции Эрмита, которые изображены на рис. 12.