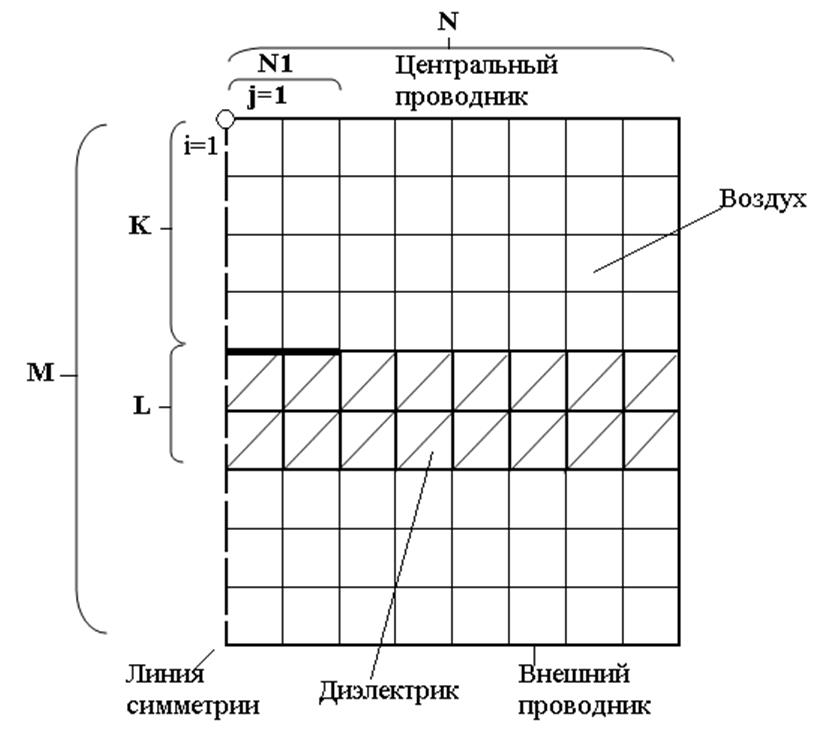
Рис. 1.4. Подобласть передающей линии с нанесенной сеткой для
расчета поля методом конечных разностей
Итак, после ввода начальных условий основная программа, во-первых, вызывает подпрограмму САР и запоминает результаты вычисления емкостей, полученные при интегрировании по замкнутому контуру вдоль внутренних и внешних проводников (для обеспечения хорошей точности оба результата должны быть как можно ближе друг к другу). Далее происходит деление ячеек и обращение к подпрограмме REC, затем вновь к подпрограмме CAP и т.д. После получения трех результатов для последовательно уменьшающихся размеров ячеек производится проверка их сходимости и путем экстраполяции находится наилучший результат. Такая процедура проделывается для случаев, когда линия заполнена и не заполнена диэлектриком, и из этих результатов определяется характеристический импеданс и фазовая скорость.
Решение уравнения Пуассона с помощью функции Грина. Решение внутренней задачи для ПЛ можно получить из уравнения Пуассона, задаваясь распределением электрических зарядов на проводниках:
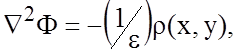
r(x,y) - объемная плотность зарядов на проводниках; Ф=0 на границе.
Для решения этого уравнения используется функция Грина G:
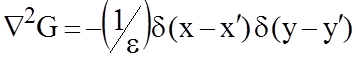 , G=0
на поверхности, (1.33)
, G=0
на поверхности, (1.33)
где d - функция Дирака.
Если решение уравнения (1.33) ищется в виде ![]() ,
то решение уравнения Пуассона будет иметь вид:
,
то решение уравнения Пуассона будет иметь вид:
![]() . (1.34)
. (1.34)
Общий заряд проводника
![]() × (1.35)
× (1.35)
Уравнения (1.34), (1.35) требуют интегрирования по граничной поверхности.
Расчёт погонных потерь в проводящих ![]() и
aдиэлектрических
и
aдиэлектрических ![]() средах
многослойных полосковых структур осуществляется по соотношениям:
средах
многослойных полосковых структур осуществляется по соотношениям:
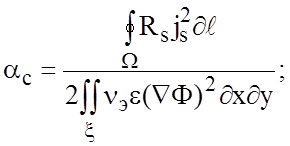
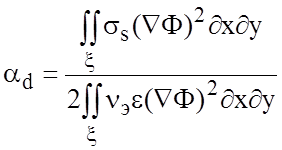 ,
,
где ![]() - периметр поперечного сечения
проводника;
- периметр поперечного сечения
проводника; ![]() - поперечное сечение ЛП;
- поперечное сечение ЛП; 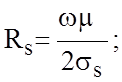
![]() -
поверхностная проводимость;
-
поверхностная проводимость; ![]() - поверхностная
плотность тока.
- поверхностная
плотность тока.
1.3. Методы синтеза полосковых линий
Математическая постановка задачи синтеза в большинстве случаев для полосковых ЛП сводится к решению нелинейного уравнения или системы уравнений (для связанных линий) относительно неизвестных геометрических размеров. Для одиночной ПЛ задача формулируется в виде
![]() .
(1.36)
.
(1.36)
При рассмотрении связанных ПЛ система нелинейных уравнений для волновых сопротивлений четного Ze и нечетного Zo типов возбуждения приводится к виду [10]:
![]() ;
;
![]() ,
,
где ![]() - вектор
конструктивных параметров;
- вектор
конструктивных параметров; ![]() -
заданные константы.
-
заданные константы.
Решение задачи при этом сводится к отысканию нулевых минимумов функции:
![]() . (1.37)
. (1.37)
Из некоторой начальной точки, которая может быть ориентировочно определена из графиков или из конструктивно-технологических соображений, осуществляется процесс движения, который, например, для метода сопряженных градиентов [11] описывается итерационным соотношением вида:
![]() ,
,
где ![]() -
субвектор конструктивных параметров
-
субвектор конструктивных параметров ![]() ; i - номер итерации.
; i - номер итерации.
При этом направление движения на (i+1) - й итерации определяется как
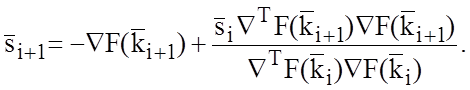
После (m+1) - й итерации (i=m) процедура циклически повторяется с заменой ![]() на
на ![]() [
[![]() - начальная точка, в которой
вычисляется
- начальная точка, в которой
вычисляется ![]() ]. Таким образом, основная
вычислительная процедура в градиентных методах оптимизации связана с
определением частных производных, которые, в основном, находятся численными
методами.
]. Таким образом, основная
вычислительная процедура в градиентных методах оптимизации связана с
определением частных производных, которые, в основном, находятся численными
методами.
Как показывают вычислительные эксперименты, для решения нелинейных уравнений (1.36), (1.37) и их аналогов наиболее эффективно использовать метод Ньютона [12], имеющий квадратичную сходимость в окрестности точки решения. Как правило, достаточно 3...6 итераций для получения решения с погрешностью по Z, Ze, Zo , меньшей 0,01 Ом.
2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ПОЛОСКОВЫХ ЛИНИЙ
2.1. Симметричная полосковая линия (СПЛ)
|
Симметричная полосковая линия (СПЛ), показанная на рис. 2.1, является одной из наиболее часто используемых линий передачи СВЧ диапазона. Основным типом волны СПЛ является Т-волна. Все ее конструктивные параметры могут быть полностью определены на основе электростатического анализа. |
Рис.2.1. СПЛ |
Если не вводить упрощение, что полосковый проводник имеет нулевую толщину, то наиболее точное значение волнового сопротивления можно получить из формул:
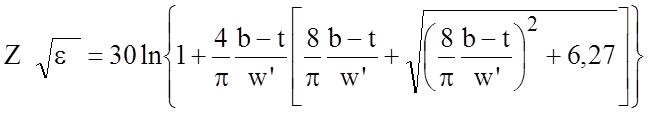 , (2.1)
, (2.1)
где
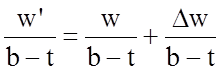 , (2.2)
, (2.2)
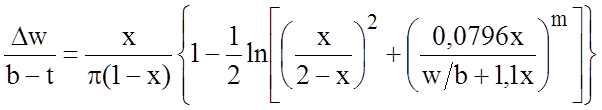 ,
,
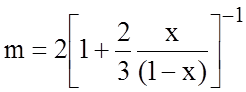 ,
, ![]() . (2.3)
. (2.3)
Для ![]() погрешность расчета по
формулам (2.1) - (2.3) составляет не более 0,5 %.
погрешность расчета по
формулам (2.1) - (2.3) составляет не более 0,5 %.
Потери в СПЛ.Суммарные потери ПЛ, определяющиеся коэффициентом затухания a, как и других типов ЛП, могут быть разделены на две составляющие - потери в проводниках и в диэлектрике:
![]()
Потери в проводниках определяются возрастанием индуктивности, обусловленным проникновением магнитного поля в проводник. Для ПЛ эти потери (дБ/м) могут быть рассчитаны по формуле :
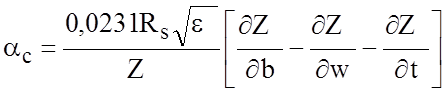 .
.
Используя выражения (2.1) - (2.3), получаем:
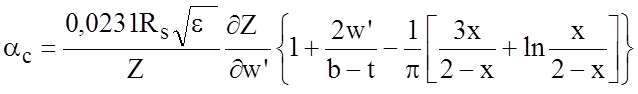 , (2.4)
, (2.4)
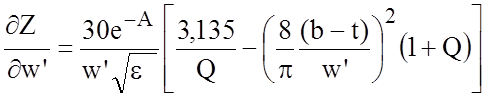 ,
,
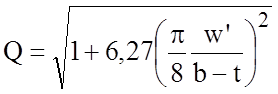 .
.
Как видно из формулы (2.4), потери в проводниках для заданного значения волнового сопротивления Z возрастают пропорционально квадратному корню из значения частоты (в соответствии с частотной зависимостью Rs).
Потери в диэлектрике СПЛ, как и любой другой с Т-волной, определяются формулой :
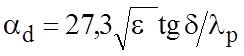 , (2.5)
, (2.5)
где tgd - тангенс угла потерь в диэлектрике; lр - длина волны в свободном пространстве для рабочей частоты.
Из уравнения (2.5) видно, что потери в диэлектрике прямо пропорциональны частоте и tgd. На СВЧ потери в диэлектрике, как правило, малы по сравнению с потерями в проводниках. Однако в миллиметровом диапазоне потери в диэлектрике становятся сравнимыми с потерями в проводниках, так как потери в диэлектрике возрастают по линейному закону, тогда как потери в проводниках пропорциональны квадратному корню из частоты.
2.2. Микрополосковая линия (МПЛ)
|
Конфигурация МПЛ показана на рис. 2.2. Волна, распространяющаяся вдоль микрополоскового проводника, является квази-Т волной. Выражения для Z и эффективной диэлектрической постоянной eэ, учитывающие влияние толщины полоскового проводника, имеют вид: |
Рис. 2.2. МПЛ |
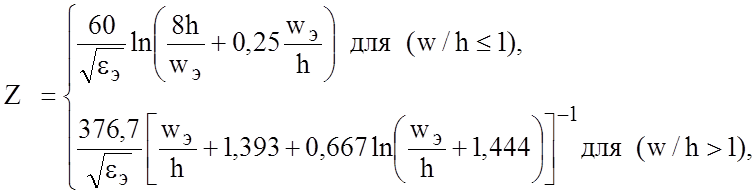 (2.6)
(2.6)
где
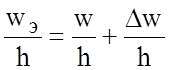 , (2.7)
, (2.7)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.