Исследование алгоритмов одномерной оптимизации. Исследование комбинаторного метода, ветвей и границ: Методические указания к лабораторным работам

Лабораторная работа № 1

ИССЛЕДОВАНИЕ АЛГОРИТМОВ ОДНОМЕРНОЙ

 ОПТИМИЗАЦИИ

1. ЦЕЛЬ РАБОТЫ

Целью настоящей работы  являются изучение и анализ поисковых алгоритмов минимизации функции одной переменной: дихотомического, Фибоначи и “золотого сечения”.

2. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

2.1. Введение

В большинстве методов поисковой оптимизации, используемых в задачах параметрического синтеза конструкций и технологических процессов, таких как методы наискорейшего или покоординатного спуска, метод сопряженных направлений и т.п., на каждом шаге приходится решать задачу минимизации функции одной переменной. Действительно, после выбора в исходной точке  (k -го шага) направления поиска  величина шага при этом направлении определяется из условия минимума целевой функции F (+ ), которая при фиксированных  и  является функцией одной из скалярной переменной F(g). В результате решения этой задачи получают значение  и следующий шаг поиска начинают из точки

    Процедура нахождения   представляет  собой задачу поисковой одномерной оптимизации. Различные методы одномерного поиска используют некоторый начальный интервал неопределенности L₀, содержащий минимум функции F(g), который затем уменьшается до некоторого значения  путем вычисления значений функции в соответствующих точках и отбрасывания заведомо не оптимальных подынтегрвалов.

    Будем для определенности рассматривать далее так называемые унимодальные функции F(g), т.е. функции, имеющие на заданном интервале [а,в] единственный минимум (рис.1). Не нарушая общности, будем полагать, что F(g) минимизируется на интервале [0,1]. Обозначим  искомое значение, доставляющее минимум F(g).

2.2. Дихотомический метод

Этот метод предполагает на каждом шаге вычисление функции в двух точках (проведение двух экспериментов). При этом с целью максимального уменьшения интервала неопределенности на каждом шаге указанные точки выбираются как можно ближе к середине интервала.

Пусть на первом шаге эксперимент проводится в точках g₁=1/2 - e/2 и g₂=1/2 - e/2 (рис.1), где e - достаточно малое положительное число (это число можно трактовать как чувствительность экспериментатора в различии двух близких точек).

 

Рис.1

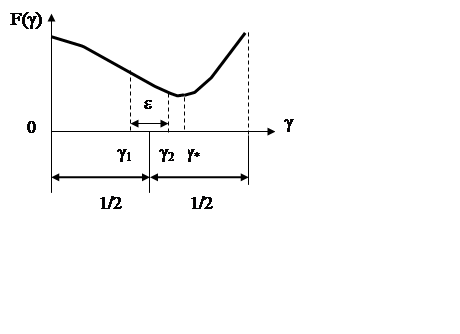Если F (1/2 -e/2)>F(1/2+e/2) то с учетом унимодальности и возможности нахождения минимума в интервале e для дальнейшего поиска должен быть оставлен интервал [1/2-e/2,1], в противном случае - [0,1/2 +e/2]. Таким образом, если в начале интервал неопределенности L₀ равен 1, то после первого шага (состоящего из двух экспериментов) он равен

                                   L₂=1/2+e/2.

Выберем теперь третий и четвертый эксперименты как e пару середине оставшегося интервала. После этого интервал неопределенности станет равным

                                   L₄=1/4+3/4e.

Легко понять, что после n экспериментов (n - четно), произведенных по тому же правилу, минимум функции   лежит в интервале

                                        (1)

Из формулы (1) видно, что для уменьшения интервала неопределенности, например до 0,01, если пренебречь величиной e, требуется 14 экспериментов.

2.3. Метод Фибоначи

Этот метод является наиболее быстрым методом поиска, требующим минимального числа экспериментов. Здесь на каждом шаге, кроме первого, проводится не два, а один эксперимент. Стратегия поиска состоит в том, что новая точка поиска располагается внутри интервала неопределенности симметрично относительно уже находящейся там точки, оставшейся от предыдущих экспериментов. Для определения требуемого числа экспериментов n , обеспечивающего точность, а также для выбора положения двух первых точек поиска, необходимо рассмотреть процесс поиска в обратном порядке, т.е. с последнего шага.

Рассмотрим ситуацию, которая возникла после того, как все эксперименты, кроме последнего, уже проведены. Длину изменяющегося интервала неопределенности обозначим . Внутри этого интервала находится эксперимент с наименьшим из (n-1)  испытаний значением функции F(g) и внутри него также, следует провести последний эксперимент. Очевидно, что для обеспечения минимального интервала неопределенности  после n экспериментов  указанные точки должны быть симметрично расположены относительно середины интервала  и удалены от нее на расстояние e/2 (рис.2).

 

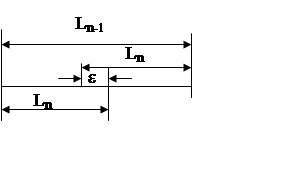Таким образом,

.                                                   (2)

Рассмотрим далее ситуацию, когда проведены все эксперименты, кро­ме двух последних, а длину имеющегося интервала неопределенности обозначим    L _n-2. Внутри этого интервала находится точка с наи­меньшим из ( П - 2) испытаний значением   F( У}, и такйа внутри него необходимо провести следующий (•/) - .1)-й &1;ои(^»ииаи'г. llo результатам этого эксперимента часть интвриала  /-/,-г   л»л'шч бш-ь огйрошенч,

а оставшаяся часть ость   L,, .^\,   . Писж>лък.у a.ip.iii;^ но i.'.iio, I'.ii.^ii i

часть будет отброшена, указанные точки должны располагаться на рав­ных расстояниях от концов интервала L „-у,  (рис.3). Но одна из то­чек внутри интервала Ь^.г   останется (рис.3) после (/7-1) акспе-р-здзнта и станет точкой внутри интервала L^-i   (ри°«2). Сочетание возможных комбинаций рис.2 и 3 приводит к схеме разбиения интервала /,д»    .изображенной на рис. 4.

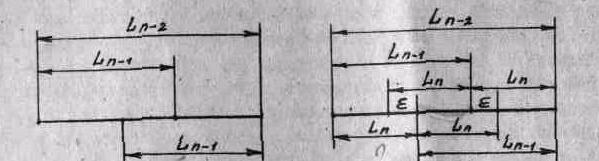
Рис. 3 Рис. 4 Из рис. 4 следует, что

1-'п-г ⁼ l-'n-i ⁺ ^п.

Лналогично

L'n-з ⁼ ^п-з. ^^п-1.

В o6ir°M случае

L^ = Lj + L^ , /= 2.3, ..., п - I.    (3)

Таким образом,

i-'^-f ⁼ —"/7 ~ "I '

Lin-a. ^s- Lin-i ⁺ Ьп ³ ЗЬг, - £, Lin-з = Ьп-г ⁺^/»-/ = У1^п~ ^z£, Ьп-ч = lifi-з +i'n-.s. ^8Ь^-Зе..

Длч полу-.ения общей фориулы длины интервала ii/i-к          вве-хе:н последов'.)- ольность чисвл Фибоначчи F' ц , определяеьую сле­дующим образом:

Го = ^ =/,    (4)

fk-f^+f^, K^2,3,...

Тогда имеем

• ' L^=F^L^ -F^e. '.; ^r ,     ^:,.^).-

Учитывая, что после первого испытания интервал неопределеннос­ти рамн I, то^;">лагая К=-П - I, получаем:

F^L, -F^^£ = /^ Отсвдз r

L.-^.^E.        C6)

Следовательно, после П   экспериментов начальные интервал но-определенности, если пренебречь величиной £ , уменьшается в Р^ раз. Для уменьшения интервала неопределенности, например до 0,01. требуется II экспериментов.