Замедляющие системы (основные свойства, характеристики, теоретические и экспериментальные методы исследования замедляющих систем): Учебное пособие, страница 7

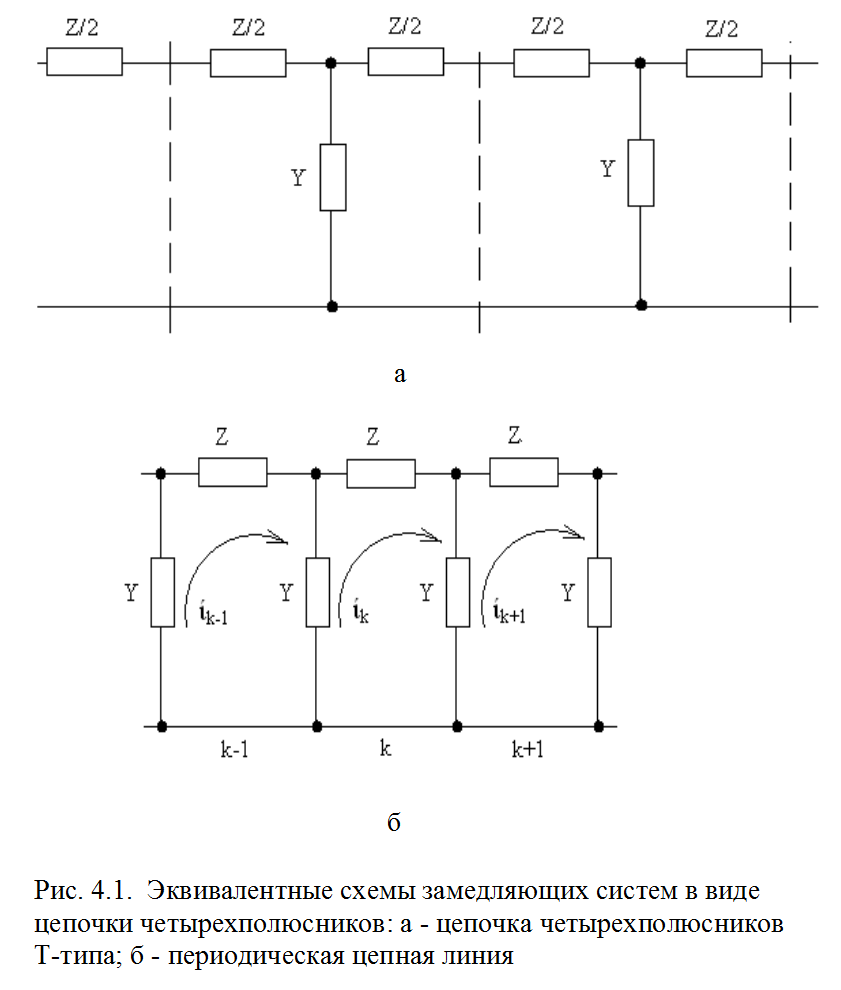
          Наиболее простыми моделями, используемыми для анализа сложных ЗС, являются эквивалентные схемы с сосредоточенными реактивными элементами [1,2]. Эффективность метода эквивалентных схем в значительной степени зависит от того, насколько точно выбранная схема соответствует исследуемой ЗС, а также от точности определения параметров элементов, образующих схему. Развитием метода эквивалентных схем является использование модели, содержащей, наряду с сосредоточенными элементами схемы, элементы с распределенными постоянными, например отрезки линий передач [3]. Метод эквивалентных схем, в котором используется простой математический аппарат из теории цепей, часто применяют для качественной, а в отдельных случаях и для количественной оценки свойств замедляющих систем. Остановимся на этом методе более подробно. Условное изображение периодической ЗС в виде цепочки четырехполюсников показано на рис. 4.1,а. Каждый четырехполюсник представляет эквивалентную схему отдельной ячейки системы из реактивных элементов Z и Y, являющихся комбинацией индуктивностей и емкостей. Характер и значение каждого элемента определяются геометрией замедляющей системы. В совокупности эквивалентная схема представляет периодическую цепную линию (рис. 4.1,б), обладающую свойствами полоснопропускаю-щего фильтра. При воздействии гармонического сигнала в такой схеме распространяются волны напряжения и тока. Причем фазовый сдвиг на период схемы соответствует изменению фазы волны на период ЗС.

          Связь между фазовым сдвигом напряжения или тока φ_L на период схемы легко устанавливается из анализа цепи.

          Определим падение напряжения по замкнутому контуру в одной из ячеек схемы с номером к. Полагаем при этом, что токи ί в соседних ячейках к - 1, к, к + 1 отличаются только фазой φ_L:

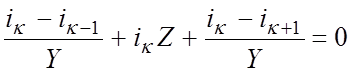,                             (4.1)

где                                       .                                (4.2)

Подставим (4.2) в (4.1) и получим

.

Так как                 ,  то

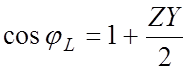 .                                                         (4.3)

Заметим, что Z и Y являются функциями частоты, следовательно, φ_L также зависит от частоты.

В теории фильтров равенство (4.3) называют условием прозрачности фильтра. Оно позволяет определить границы полосы, а также зависимость φ_L от частоты.

Рассмотрим некоторые свойства ЗС, вытекающие из уравнения (4.3). Поскольку cos φ_L удовлетворяет неравенству , то из (4.3) следует, что

.                                        (4.4)

Обратим внимание, что ZY не положительно. Это свидетельствует о разном характере реактивностей Z и Y в полосе частот, границы которой определяются неравенством (4.4). Граничные частоты фильтра соответствуют границам полосы частот соответствующей ЗС.     Уравнение

                                                                                                   (4.5)

определяет граничную частоту ω₀, при которой φ_L = 0 + 2πр, где р = 0, ± 1, ± 2, … – целые числа.

          Второе уравнение

                                                                                       (4.6)

определяет вторую граничную частоту ω_π , при которой φ_L = π + 2πр.

Равенство (4.3) в совокупности с уравнением (4.2) позволяет также построить дисперсионные характеристики и определить их основные свойства. Пример применения метода эквивалентных схем будет приведен ниже применительно к ЗС типа цепочки связанных резонаторов.

4.2.  Спиральная замедляющая система

4.2.1.  Дисперсионные характеристики

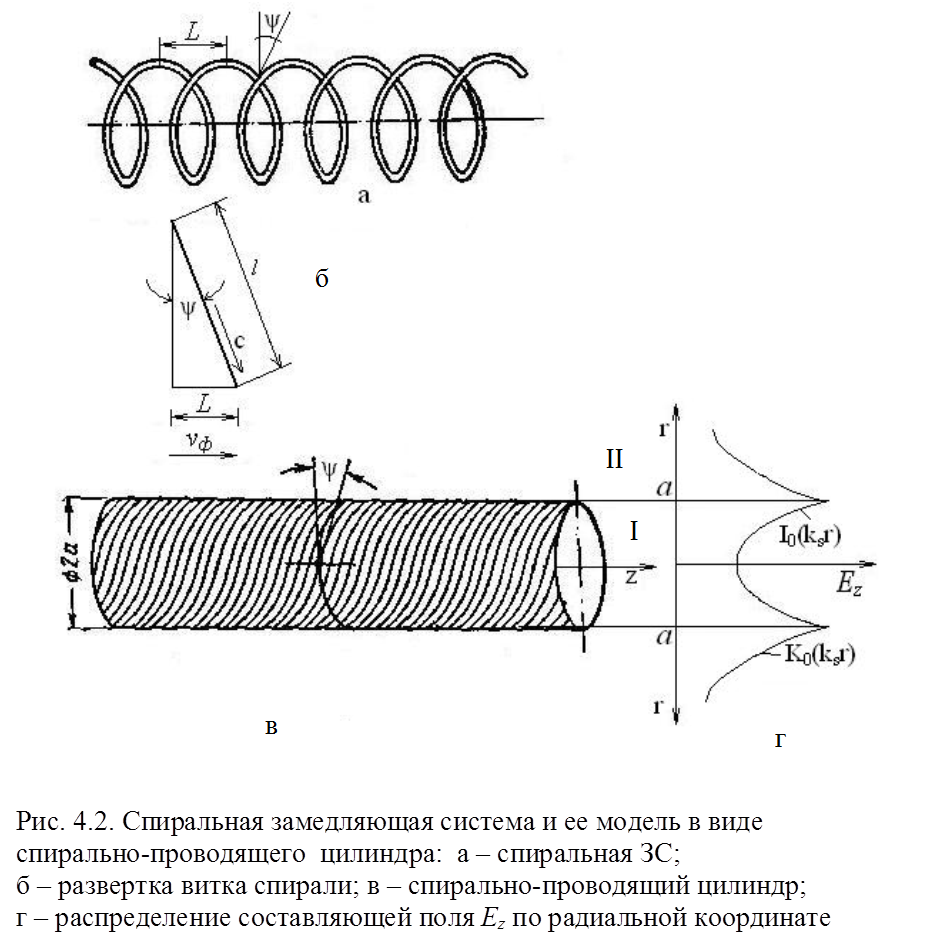
Рассмотрим простейшую спираль, выполненную из тонкого идеального проводящего проводника, имеющую малый период, так что    L << λ₃ . Экран отсутствует. Спираль с обозначением размеров показана на рис. 4.2,а.

Процесс замедления можно объяснить из простейших соображений, если считать, что электромагнитное поле сосредоточено вблизи витков спирали и волна распространяется вдоль проводника, огибая каждый виток спирали со скоростью света. Одновременно волна распространяется и в продольном направлении вдоль оси z со скоростью меньше скорости света во столько раз, во сколько длина витка больше шага спирали. Сказанное поясняется рисунком 4.2,б. Следовательно,

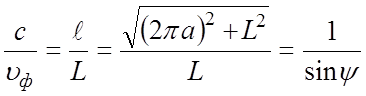                               .                                     (4.7)

         

Как будет видно в дальнейшем, расчет замедления с помощью такого грубого представления дает неплохие результаты на достаточно высоких частотах, когда поле действительно сосредоточено вблизи витков. В общем же случае в спирали имеет место зависимость распределения поля в поперечном сечении от частоты и, как следствие, дисперсия волн.

 Подробно свойства спирали могут быть изучены с помощью модели сплошного цилиндра, проводящего только в направлении намотки витков спирали, то есть под углом ψ к плоскости, перпендикулярной к оси z(модель спирально проводящего цилиндра показана на рис. 4.2,в.). Таким образом, цилиндр представляет сплошную проводящую поверхность, но обладающую изотропной проводимостью.

Для определения полей в такой модели разобьем область распространения волны на две частичные области: область I – внутри цилиндра   r <  и область II – вне цилиндра r> . Как было показано в разделе 1, поле в системе с осевой симметрией описывается модифицированными функциями Бесселя первого и второго рода. В частности, выражения для продольных составляющих электрического и магнитного полей имеют вид:

            ,   ,            (4.8)

где А, В, С, D – произвольные постоянные; множитель здесь и в дальнейшем опущен. С учетом конечности значений полей в любой точке ЗС и свойств функций I₀  и K₀ следует принять: в области I – В = 0,  D = 0; в области II – А = 0, С = 0. Следовательно, выражения для полей Е_z   и   H_z принимают следующий вид:

в области I:                                                    в области II:

,                                              ,