Лабораторная работа №2
При цифровом моделировании непрерывных систем необходимо обеспечить близость процессов в моделируемой непрерывной системе и в ее цифровой реализации. Несовпадение этих процессов связано с двумя причинами: 1) заменой непрерывного входного процесса цифровым и 2) использованием численных методов анализа.
При замене непрерывного процесса цифровым возникают ошибки из-за квантования по уровню (шумы квантования) и дискретизации по времени (ошибки восстановления непрерывного процесса по его дискретным отсчетам). Шумы квантования считаются случайным процессом с дисперсией h2/12, где h – величина шага квантования. При 16-разрядном двоичном представлении числа шаг квантования равен примерно одной 65-тысячной этого числа. Поэтому шумами квантования можно пренебречь. Восстановить непрерывный процесс по его дискретным отсчетам можно без ошибки согласно теореме Котельникова, если спектр этого процесса ограничен частотой fгр (S(f) = 0 при f> fгр) и частота дискретизации fдискр ³ 2fгр. При функциональном моделировании систем частоту дискретизации обычно берут много больше fгр: fдискр = (10 – 20)fгр, где fгр = fв – верхняя частота спектра, т. е. частота, на которой спектр процесса спадает до достаточно малой величины.
Математическая модель непрерывной системы представляет собой или нелинейное дифференциальное уравнение (в системах компьютерной математики) или совокупность соединенных между собой линейных и нелинейных блоков (в системах визуального моделирования).
Разработано большое количество методов численного решения дифференциальных уравнений. Рассмотрим, как производится численное решение на примере нелинейного дифференциального уравнения первого порядка вида du/dt = f(u,t). Решение находится для дискретных значений аргумента, отличающихся на шаг интегрирования Dt. В одношаговых разностных методах для нахождения следующего значения uк = u(tк) требуется информация только об одном предыдущем шаге. Из одношаговых методов наибольшую известность получили методы Рунге-Кутта. В основу метода Рунге-Кутта первого порядка, называемого также явным методом Эйлера, положено разложение функции u(t) в ряд Тейлора в окрестности точки (tk-1,, uk-1), ограниченное двумя первыми членами ряда: uk = uk – 1 + Dt*u'k-1, где u'k-1 = du(t)/dt при t = tr-1. Так как du(t)/dt = f(u,t), то uk =uk – 1+Dt*f(uk – 1,tk –1). Видим, что при использовании этого метода считается, что в течение времени Dt функция u(t) изменяется линейно и тангенс угла наклона прямой равен u'k-1. Это, как показано ниже на рисунке, приводит к ошибке (сплошные линии).
Неявный (обратный) метод Эйлера основан на разложении
функции u(t) в ряд Тейлора в окрестности точки (tk,, uk).
Расчет ведется по выражению uk = uk – 1 + Dt*u'k
= uk – 1 + Dt*f(uk,tk). Решение
находится тоже с ошибкой, хотя и другого знака (пунктирная линия на  рисунке). Ошибка увеличивается с увеличением шага Dt=
tk
- tk-1. Для уменьшения
этой ошибки при неизменном Dt используют методы Рунге-Кутта более высокого порядка.
При большом шаге вычислительный процесс может стать неустойчивым.
рисунке). Ошибка увеличивается с увеличением шага Dt=
tk
- tk-1. Для уменьшения
этой ошибки при неизменном Dt используют методы Рунге-Кутта более высокого порядка.
При большом шаге вычислительный процесс может стать неустойчивым.
VisSim является пакетом визуального моделирования, поэтому задать модель аналитически в виде нелинейного дифференциального уравнения нельзя. Нужно по дифференциальному уравнению составить функциональную схему, или графическую модель. Для дифференциального уравнения du/dt = f(u,t) она составляется следующим образом. Сначала формируется f(u,t) нелинейным блоком, на входы которого подаются tи u. Так как f(u,t) является производной процесса u(t), то сам процесс u(t) получается интегрированием выходного процесса нелинейного блока. Получившаяся графическая модель показана на рисунке ниже.
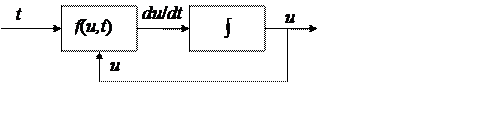


|
|
Нужно быть очень внимательным при выборе шага модельного времени, когда моделируются замкнутые системы. В этих системах текущее значение входного процесса сравнивается со значением выходного процесса, рассчитанного по предыдущим значениям входного процесса. Это экстраполированное значение не должно значительно отличаться от входного процесса. В противном случае возникают большие ошибки моделирования, а при большом шаге процесс может стать неустойчивым. Чтобы результаты моделирования были удовлетворительными, можно пользоваться следующим правилом: за интервал, равный шагу модельного времени, переходная характеристика должна изменяться на величину, много меньшую установившегося значения. На практике шаг моделирования надо брать таким, чтобы при его уменьшении процессы в модели практически не изменялись.
Выполнение работы
1. Исследование ошибок численного решения дифференциального уравнения.
1.1 Составить графическую модель для дифференциального уравнения согласно заданию:
|
Вариант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Уравнение |
du/dt = at2 + bu |
du/dt = at(1 + bu) |
du/dt = at2 + but |
|||||||
|
a |
1 |
2 |
2 |
0,5 |
0,7 |
1 |
1 |
1 |
2 |
2 |
|
b |
2 |
2 |
1 |
3 |
2 |
1 |
1 |
2 |
1 |
2 |
1.2. Собрать на рабочем столе VisSim составленную модель. Запомните, что различные методы численного интегрирования реализуются только для моделей, в которые входят интеграторы, обозначаемые как 1/S (Blocks → Integration → integrator). Интегратор можно реализовать и по-другому – как линейное устройство, задаваемое передаточной функцией (Blocks → Linear System → transferFunction), если установить в числителе (Numenator) – 1, а в знаменателе (Denominator) – 1_0. Но для такого интегратора, охваченного обратной связью, реализуется только метод Эйлера. Для удобства изображения линии обратной связи использовать указатель (Blocks → Annotation → wirePozitioner). Его нужно перевернуть (Edit → Rotate 180).
1.2. Задать условия моделирования (Simulate → Simulation Setup): в окне Simulation Setup задать шаг Step Size – 0.0001, время моделирования Range End – 2.1. В области Integration Algoritm активировать метод Рунге-Кутта 4-го порядка. Запустить моделирование. Считаем, что полученное решение близко к точному. Замерить значения процесса при t = 1 с и 2 с ( с точностью до четвертой значащей цифры после запятой). Для более точного измерения использовать “лупу”. Для этого надо выполнить следующие действия: нажать и удерживать клавишу Ctrl; с помощью указателя мыши выделить требуемую область осциллограммы; отпустить клавишу мыши; отпустить клавишу Ctrl. Для считывания координат использовать перекрестие (Правой клавишей мыши щелкнуть на Plot; в раскрывшемся окне левой кнопкой мыши щелкнуть на Read Coordinates). Если требуется возвратиться к исходному масштабу, проделать следующие действия: нажать и удерживать клавишу Ctrl; навести указатель мыши на окно; щелкнуть правой кнопкой мыши (или двойной щелчок левой); отпустить клавишу Ctrl.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.