Информатика и выч. техника \ Информационные технологии в металлургии

Технологии реализации алгоритмов методов и решения задач оптимизации средствами Excel: Методические указания к выполнению практических занятий, страница 3

Результаты решения задачи для условий, описанных выше, приведены на рис. 2.4.

Задача 3.

Постановка задачи. Cоставить алгоритм нахождения с требуемой точностью e экстремума функции f(X) двух переменной градиентным методом с адаптацией шага.

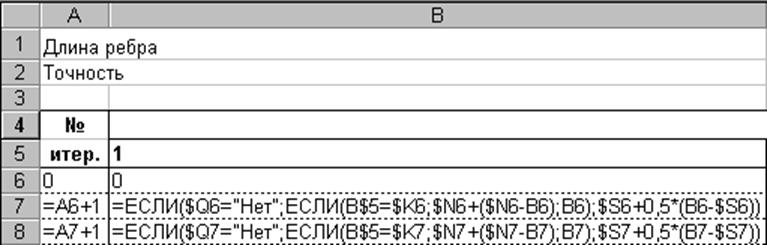
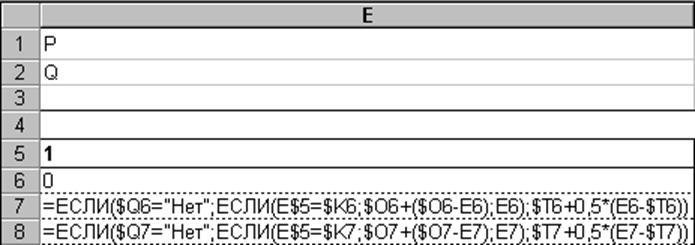
Рис. 2.3. Содержание ячеек при реализации симплекс-метода

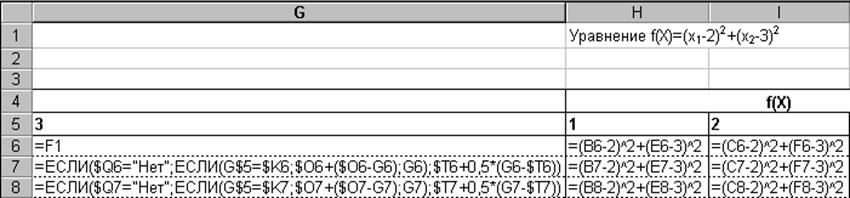
Продолжение рис. 2.3


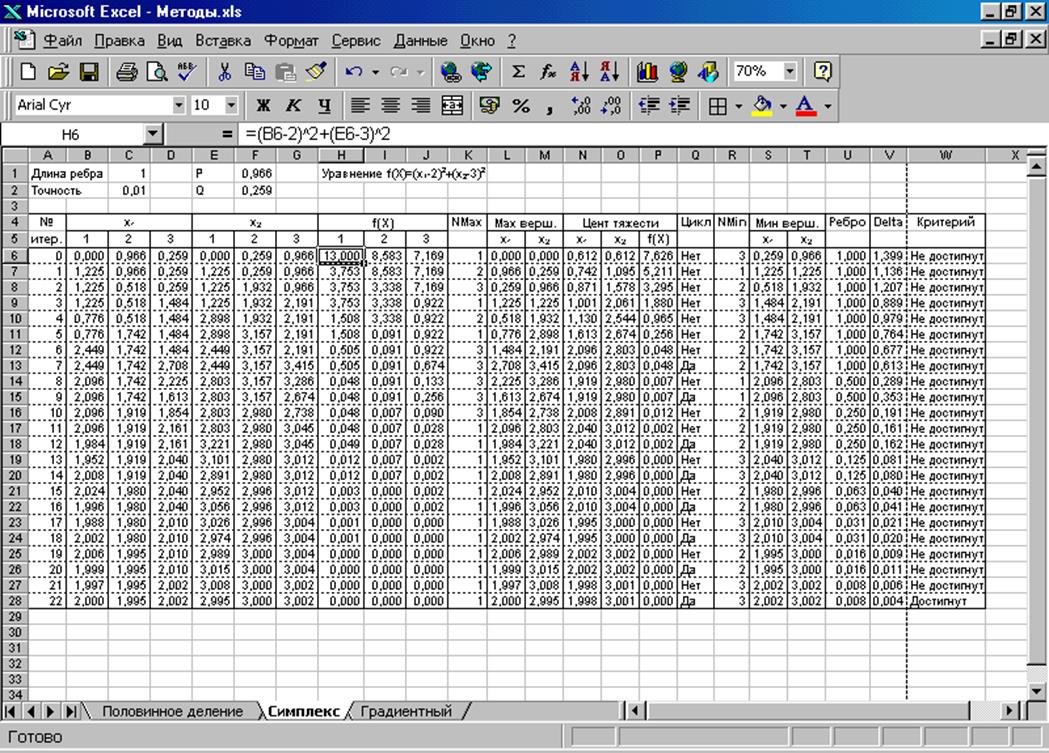
Рис. 2.4. Результаты реализации симплекс-метода


Алгоритм метода.

1. Начальный этап. Задают начальную точку X(0), начальный шаг l(0), k = 0.

2. Расчет параметров метода на k-ой итерации. Рассчитываются значения функции, первых производных. Определяются единичные направления по выражению

,    .

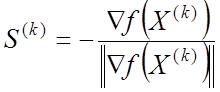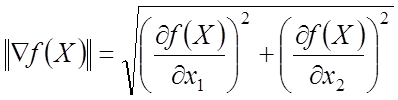Определяется текущее направление движения Napr по таблице

s1

s2

Napr

>0

>0

ArcTn(s2/s1)/p×180

>0

<0

ArcTn(s2/s1)/p×180+360

<0

>0

ArcTn(s2/s1)/p×180+180

<0

<0

ArcTn(s2/s1)/p×180+180

Если k = 0, то переход к этапу 4, иначе к этапу 3.

3. Проверка условия окончания метода и адаптация шага.

Если |f(X(k)) - f(X(k-1))| £ e, то переход к этапу 5.

Определение угла между направлениями на k-ом и (k-1)-ом шагах q = |Napr(k) - Napr(k-1)|.

Расчет коэффициента шага a, например по следующей таблице

q

a

<90

2 - q/90

>90

0,5 + (180 - q)/90×0,5

Определение шага l(k) = a × l(k-1)

4. Определение координат новой точки. Производится по формуле

X(k+1) = X(k) + l(k)×S(k)

Установить k = k + 1 и перейти к этапу 2.

5. Вывод результатов. За оптимальное решение принять X(k) точку.

Реализация метода. На рис. 2.5 приведено содержание ячеек рабочего листа, используемых для осуществления первых двух итераций при нахождении данным методом минимума функции
f(X) = (x1 - 2)4 + (x1 - 2x2)2 при начальной длине шага, равной 0,5, и точности поиска 0,001.

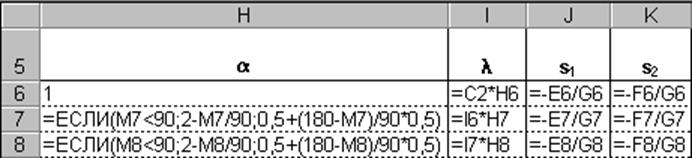
Рис. 2.5. Содержание ячеек при реализации градиентного метода

Результаты решения задачи для условий, описанных выше, приведены на рис. 2.6.

Задача 4.

Постановка задачи. Решить задачу многомерной условной оптимизации с использованием инструмента “Поиск решения”.


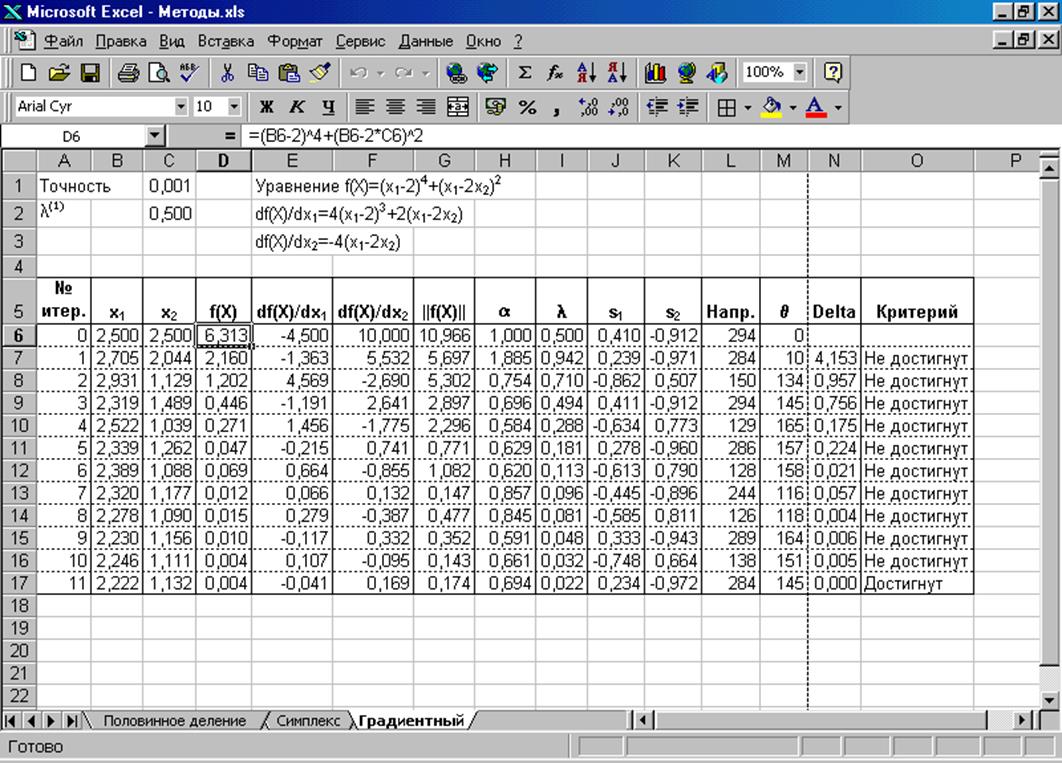
Рис. 2.6. Результаты реализации градиентного метода


Порядок решения.

1. Переход от содержательной постановки задачи к математической записи целевой функции и ограничений для задач линейного программирования в виде

 ,

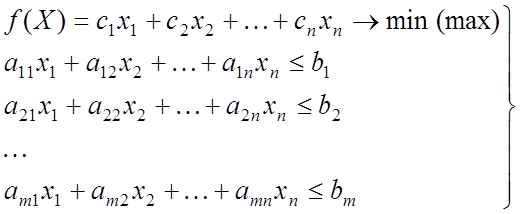где   n, m     -   число переменных и ограничений соответственно,

а для задач нелинейного программирования в виде

,

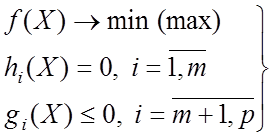где m, p       -   число ограничений-равенств и общее число ограничений соответственно.

2. Реализация математической записи задачи в ячейках рабочего листа

3. Построение задачи оптимизации с помощью инструмента “Поиск решения”.

4. Выполнение процедуры оптимизации и сохранение полученных результатов.

Реализация метода. На рис. 2.7 приведено содержание ячеек рабочего листа, реализующих математическую запись задачи линейного программирования вида

,

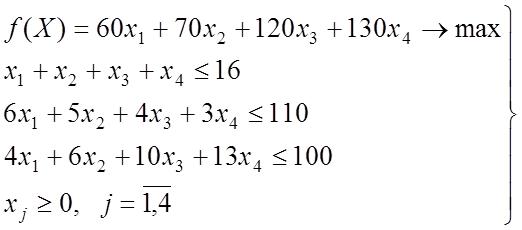Рис. 2.7. Содержание ячеек при реализации задачи
линейного программирования

а на рис. 2.8 – содержание ячеек при реализации задачи нелинейного программирования вида

.

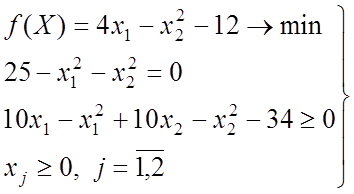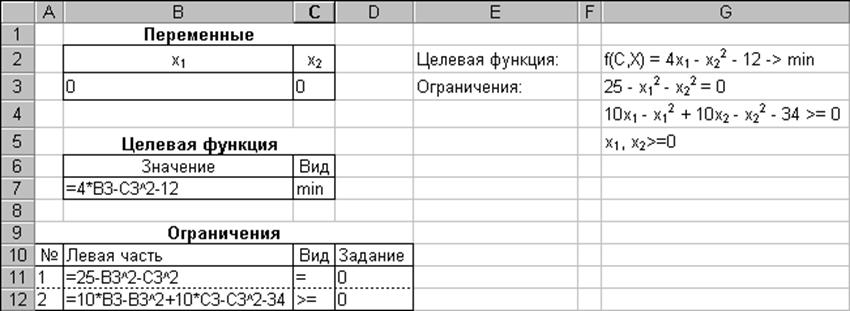
Рис. 2.8. Содержание ячеек при реализации задачи
нелинейного программирования

На рис. 2.9, 2.10 показаны построение задач оптимизации и полученные результаты для приведенных выше задач.


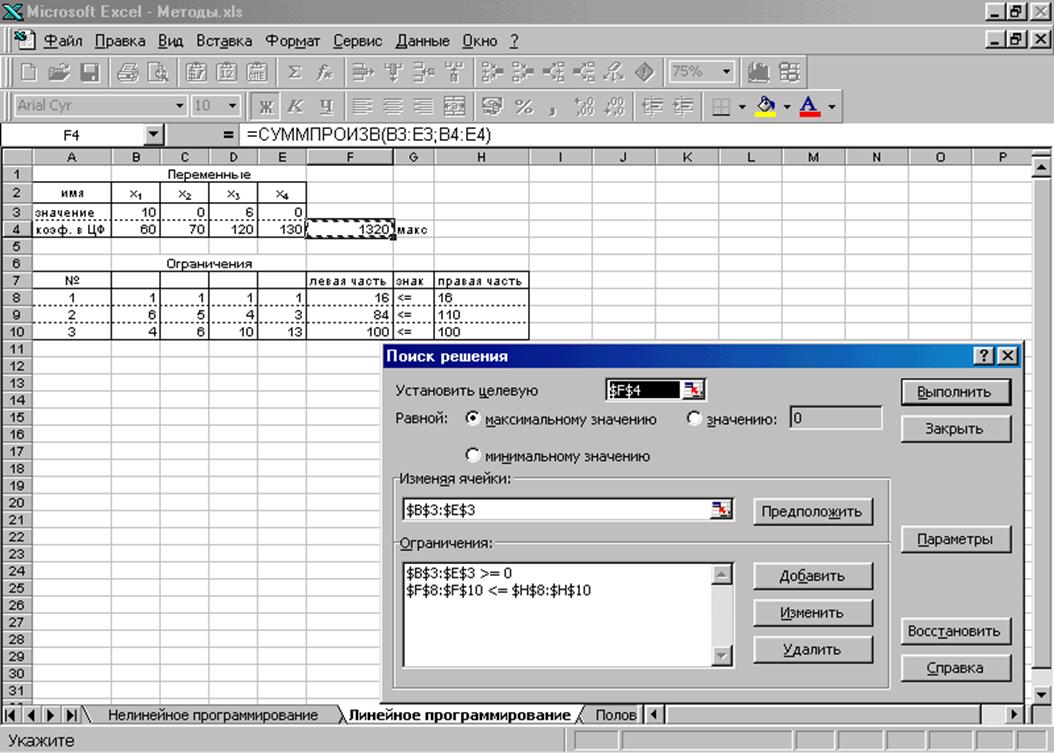
Рис. 2.9. Линейное программирование. Построение задачи оптимизации и полученные решения

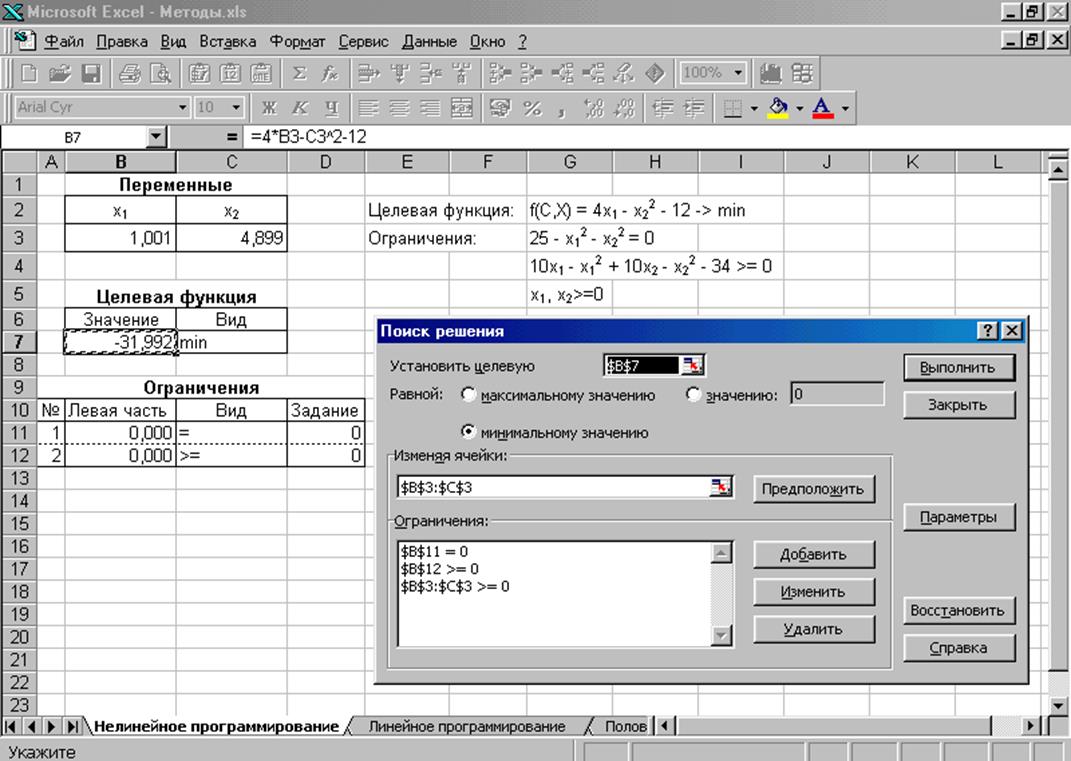
Рис. 2.10. Нелинейное программирование. Построение задачи оптимизации и полученные решения


3. Варианты заданий для выполнения практических занятий

В таблице 3.1 приведены варианты заданий для выполнения первого занятия по решению задач одномерной оптимизации с применением стандартных средств табличного процессора Excel.

Таблица 3.1

Варианты заданий первого занятия

№

Вид функции f(x)

Наименование метода

1

x2 - 2x + 1

золотое сечение

2

x2 + 3x - 7

золотое сечение

3

5x2 + x - 1

золотое сечение

4

3x2 + 2x - 1

золотое сечение

5

2x2 - x + 5

золотое сечение

6

9x2 + 5x - 3

золотое сечение

7

3x2 + 8x + 2

золотое сечение

8

x2 - 2x + 1

локализация оптимума

9

x2 + 3x - 7

локализация оптимума

10

5x2 + x - 1

локализация оптимума

11

3x2 + 2x - 1

локализация оптимума

12

2x2 - x + 5

локализация оптимума

13

9x2 + 5x - 3

локализация оптимума

14

3x2 + 8x + 2

локализация оптимума

15

x2 - 2x + 1

Фибоначчи

16

x2 + 3x - 7

Фибоначчи

17

5x2 + x - 1

Фибоначчи

18

3x2 + 2x - 1

Фибоначчи

19

2x2 - x + 5

Фибоначчи

20

9x2 + 5x - 3

Фибоначчи

21

3x2 + 8x + 2

Фибоначчи

22

x2 - 2x + 1

Обратного переменного шага

23

x2 + 3x - 7

Обратного переменного шага

24

5x2 + x - 1

Обратного переменного шага

25

3x2 + 2x - 1

Обратного переменного шага
Скачать файл