Логические функции. Словесное, табличное, алгебраическое, схемное, графическое представление логических функций, страница 2

((A→B)B)→A

F₄. Запрет по X₁ (отрицание импликации, рис.1.19). Обозначается «D».

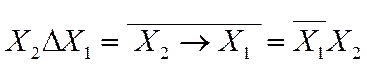F₆. Сложение по модулю 2 (исключающее ИЛИ, неравнозначность). Обозначается «Å».

Высказывание F=X₁Å X₂истинно тогда и только тогда, когда истинно или X₁или X₂.

В общем случае: Функция F (X₁, X₂,…, X _n) равна единице, если равен единице только один аргумент (рис. 1.3.10, 1.3.11).

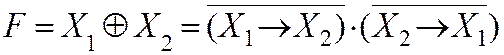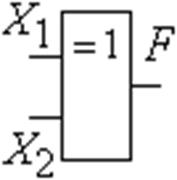
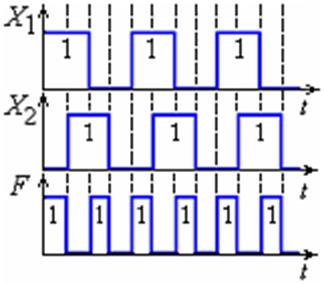
Рис. 1.3.10 Временные диаграммы операции сложение по модулю 2

Рис. 1.3.11 Обозначение операции сложение

по модулю 2. Элемент М2

F₇. Логическая связка, соответствующая союзу «или», называется дизъюнкцией (операция «ИЛИ», логическое сложение). Она обозначается «Ú», или « + », или «È».

Высказывание F =X₁+X₂истинно тогда и только тогда, когда истинно, по крайней мере, одно из высказываний X₁ или X₂ (рис.1.3.12 -1.3.15).

В общем случае: Функция F (X₁, X₂,…, X _n) равна единице, если равен единице хотя бы один аргумент (равна нулю, если равны нулю все аргументы).

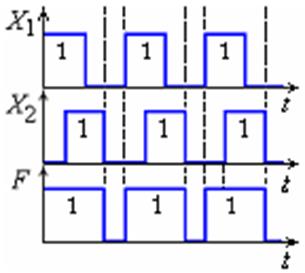
Рис. 1.3.12 Временные диаграммы операции ИЛИ

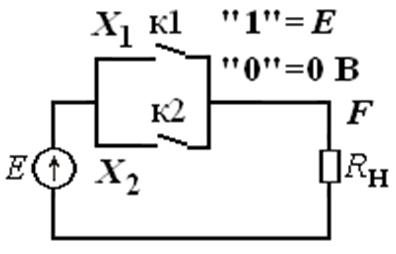
Рис. 1.3.13 Реализация операции ИЛИ на нормально разомкнутых контактах К1 и К2 двух реле. При включении реле (1) контакт замыкается (1), и наоборот

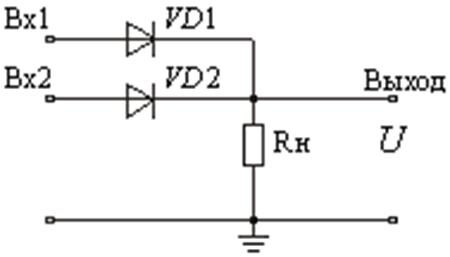
Рис. 1.3.14 Реализация элемента 2 ИЛИ. При подаче на оба входа сигналов логического нуля диоды VD1, VD2 закрыты. На выходе потенциал U, равный нулю. Если хотя бы на один вход подать потенциал логической единицы, то соответствующий диод откроется и логическая единица появится на выходе.

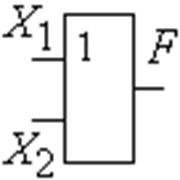
Рис.1.3.15 Обозначение операции ИЛИ.

Элемент 2ИЛИ,

где 2 - число входов

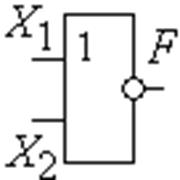F₈. Стрелка Пирса (отрицание дизъюнкции, операция ИЛИ-НЕ).

Обозначается «↓».

Функция F = X₁ ↓ X₂истинна тогда и только тогда, когда значения

всех переменных ложны (рис.1.3.16).

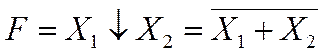Рис. 1.3.16 Обозначение операции стрелка Пирса. Элемент 2ИЛИ-НЕ, где 2 - число входов

F₉. Эквивалентность. Обозначается «~», или «º».

Высказывание X₁~X₂истинно тогда и только тогда, когда высказывания X₁ и X₂или одновременно истинны, или одновременно ложны (рис. 1.3.17).

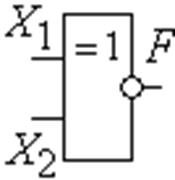Иначе: функция F = X₁~ X₂истинна, когда истинность X₁

влечет истинность X₂и обратно, истинность X₂влечет

истинность X₁ (справедливы высказывания X₁→X₂ и X₂→X₁).

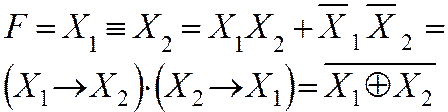Рис. 1.3.17 Обозначение операции и элемента эквивалентность

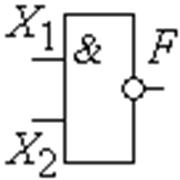F₁₄. Штрих Шеффера (отрицание конъюнкции, операция И-НЕ):

Обозначается «/».

Функция F = X₁ / X₂истинна тогда и только тогда, когда

истинны все переменные (рис.1.3.18).

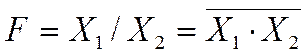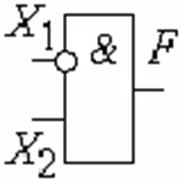
Рис. 1.3.18 Обозначение операции штрих Шеффера. Элемент 2И-НЕ

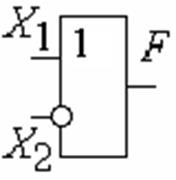
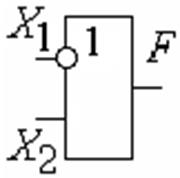
Элемент запрет по X₁: Элементы ЕСЛИ, ТО:

Рис. 1.3.19 Обозначение операции запрет по X₁. Элемент НЕТ

Рис. 1.3.20 Обозначение операции импликация.

Элементы ЕСЛИ, ТО

F₀, F₁₅. Константы 0 и 1. Специальных элементов для их генерации нет.

F₃,F₅. Повторители переменных X₁ и X₂ (рис. 1.3.1).

F₁₀, F₁₂. Отрицание X₁ и X₂(рис. 1.3.2).

Из таблицы 1.3.2 следует:

- Каждая функция с номером, изменяющимся от 0 до 7, является инверсной для функции с номером, изменяющимся от 15 до 8. Например, F₀, F₁₅ – константы 0 и 1 соответственно, являются инверсными друг другу. Те же соотношения между конъюнкцией F₁ и штрихом Шеффера F₁₄.

- Инверсия значений переменных ведет к инверсии функций.

- для получения одних функций могут использоваться другие.

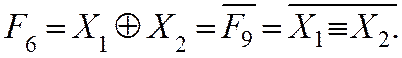Пример: реализовать функцию исключающее ИЛИ на элементах инверсии и эквивалентности (рис.1.3.21):

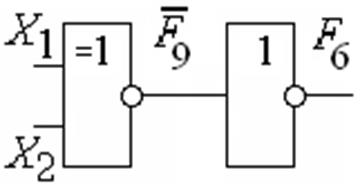
Рис. 1.3.21 Схема реализации функции исключающее ИЛИ

на элементах инверсии и эквивалентности

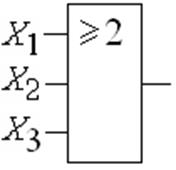
Среди операций многих переменных чаще всего упоминается функция мажор (обозначается символом #). Мажоритарные логические элементы используются для повышения надежности и помехоустойчивости цифровых устройств (рис. 1.3.22). Они имеют нечетное количество входов n, больше двух, и выход, состояние которого определяется по значению логических сигналов на большинстве входов (если больше единиц, то 1, если нулей – то 0):

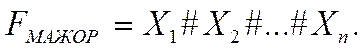Рис.1.3.22 Обозначение

операции мажор (n= 3)

Пример:

Составить логическое выражение и таблицу истинности для словесной формы задания логической функции:

Имеет ли яблоко красный цвет, если оно спелое и известно, что, если яблоко красное, то оно спелое?

Обозначение: A: яблоко красное; B – яблоко спелое. Результат: F.

Первая посылка: если яблоко красное A, то оно спелое B.

Вторая посылка: яблоко спелое B.

Следствие: яблоко красное A.

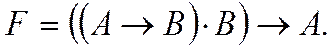С помощью данного выражения составлена таблица истинности (Табл. 1.3.3).

Таблица истинности Таблица 1.3.3

1 2

Скачать файл