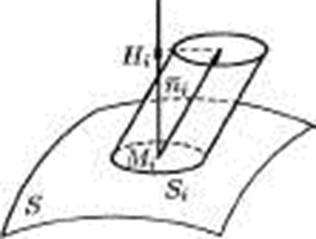
Рисунок 4.3
Приблизно вважатимемо кожний майданчик плоским, а вектор а постійним
і однаково
направленим в кожній точці майданчика. Тоді за одиницю часу через Si протікає
кількість рідини, що приблизно дорівнює Ki ![]() Hi
Hi ![]() S
S![]() , де
, де ![]() S
S![]() -площа і-го майданчика, Hi-висота i-го
циліндра зі створюючою а(Mi). Але Hi є проекцією вектора а(Mi)) на нормаль п
-площа і-го майданчика, Hi-висота i-го
циліндра зі створюючою а(Mi). Але Hi є проекцією вектора а(Mi)) на нормаль п![]() : Hi = а(Mi) , де п
: Hi = а(Mi) , де п![]() — одиничний вектор
нормалі до поверхні в точці Mj. Отже, загальна кількість рідини, що протікає
через всю поверхню S за одиницю часу, знайдемо, обчисливши суму
— одиничний вектор
нормалі до поверхні в точці Mj. Отже, загальна кількість рідини, що протікає
через всю поверхню S за одиницю часу, знайдемо, обчисливши суму
К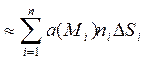 .
.
Точне значення шуканої кількості рідини набудемо, взявши межу знайденої суми при необмеженому збільшенні числа елементарних майданчиків і наближенні до нуля їх розмірів (діаметрів di майданчиків):
K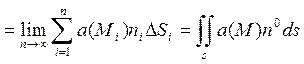
Незалежно від фізичного тлумачення поля а(М) одержаний інтеграл називають потоком векторного поля.
Потоком вектора ![]() через поверхню S називається
поверхневий інтеграл 1-го роду по поверхні S від скалярного добутку вектора
через поверхню S називається
поверхневий інтеграл 1-го роду по поверхні S від скалярного добутку вектора ![]() на одиничний вектор
нормалі до поверхні
на одиничний вектор
нормалі до поверхні ![]() .
.
![]() .
.
Обчислити потік вектора – це обчислити поверхневий інтеграл 1-го роду.
Властивості потоку
1) Потік вектора величина скалярна.
2) Потік змінює
знак на протилежний зі зміною орієнтації поверхні (тобто зі зміною орієнтації
нормалі ![]() до поверхні S):
до поверхні S):
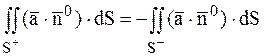 ,
,
де ![]() - сторона поверхні S, на якій вибрана нормаль
- сторона поверхні S, на якій вибрана нормаль ![]() ,
, ![]() - сторона поверхні S, на якій нормаль
- сторона поверхні S, на якій нормаль ![]() .
.
3) Властивість лінійності:
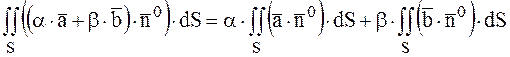 ,
,
де ![]() і
і ![]() - числа.
- числа.
4) Властивість адитивності:
якщо поверхня S складається з декількох
гладких частин ![]() ,
, ![]() , ...
, ... ![]() , то потік векторного поля
вектора
, то потік векторного поля
вектора ![]() через S дорівнює сумі потоків вектора
через S дорівнює сумі потоків вектора ![]() через поверхні
через поверхні ![]() ,
, ![]() , ...
, ... ![]() :
:
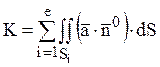 .
.
Нехай поверхня S замкнена і обмежує деяку область ![]() . Візьмемо зовнішню нормаль і
розглянемо потік зсередини поверхні S.
. Візьмемо зовнішню нормаль і
розглянемо потік зсередини поверхні S.
Коли векторне
поле ![]() представляє поле швидкостей рідини,
величина потоку дає різницю між кількістю рідини, що витікає з області
представляє поле швидкостей рідини,
величина потоку дає різницю між кількістю рідини, що витікає з області ![]() , і кількістю рідини, яка
впадає в цю область. Якщо К=0, то в область
, і кількістю рідини, яка
впадає в цю область. Якщо К=0, то в область ![]() втікає стільки ж рідині, скільки і
витікає. Так буде для будь-якої області, розташованої в потоці води.
втікає стільки ж рідині, скільки і
витікає. Так буде для будь-якої області, розташованої в потоці води.
Якщо К>0, то
витікає рідині більше, ніж втікає, тобто в області ![]() є джерела, що живлять потік
рідини.
є джерела, що живлять потік
рідини.
Якщо К<0, то витікає рідині менше ніж втікає, тоді в області є стоки, де рідина видаляється з потоку.
Приклад 4.4Знайти потік векторного поля ![]() через трикутник, вирізаний з площини
Р координатними площинами, в тому напрямку нормалі до площини, який утворює з
віссю oz тупий кут. Рівняння площини
Р: 2x-y+5z-10=0
через трикутник, вирізаний з площини
Р координатними площинами, в тому напрямку нормалі до площини, який утворює з
віссю oz тупий кут. Рівняння площини
Р: 2x-y+5z-10=0
Рішення.
Знайдемо орт
нормалі ![]() до площини Р:
до площини Р:
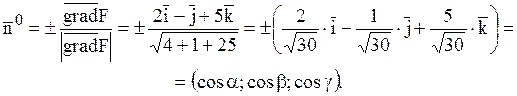
Оскільки за
умовою задачі кут між ![]() і віссю oz тупий, то
і віссю oz тупий, то ![]() <0, тому вибираємо знак «-»
<0, тому вибираємо знак «-»
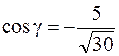 , тоді
, тоді 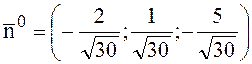 .
.
Знайдемо ![]() :
:
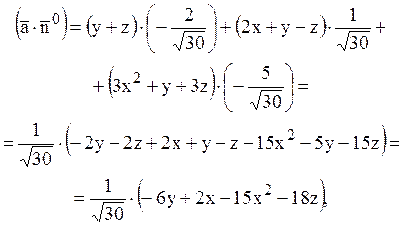
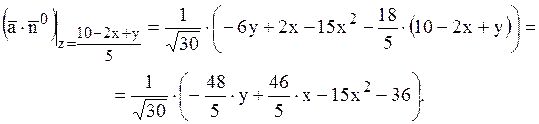
Тоді,
оскільки 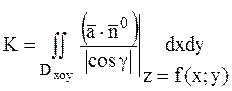 , то
, то
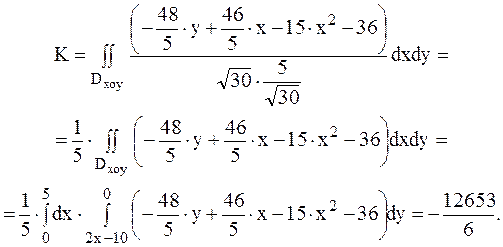
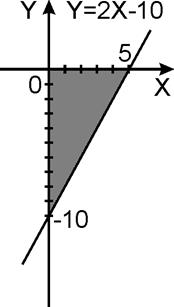
Рисунок 4.4
4.3.3 Формула Остроградського – Гауса
Якщо в деякій
області D простору координати вектора ![]() безперервні і мають
безперервні частинні похідні
безперервні і мають
безперервні частинні похідні ![]() ,
, ![]() ,
, ![]() , то потік вектора
, то потік вектора ![]() через будь-яку замкнену
поверхню S, розташовану в області D, дорівнює потрійному інтегралу від
через будь-яку замкнену
поверхню S, розташовану в області D, дорівнює потрійному інтегралу від ![]() по області V, обмеженої поверхнею S, тобто
по області V, обмеженої поверхнею S, тобто
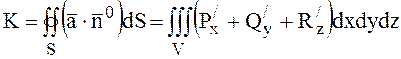 .
.
Обчислення потоку за формулою Остроградського – Гауса значно полегшує знаходження потоку, коли поверхня S замкнена.
Приклад 4.5 Знайти потік вектора ![]() через зовнішню сторону
поверхні, що розташована в першому октанті й складається з параболоїда
обертання z=x
через зовнішню сторону
поверхні, що розташована в першому октанті й складається з параболоїда
обертання z=x![]() +y
+y![]() , циліндра x
, циліндра x![]() +y
+y![]() =1 та координатних площин якщо
=1 та координатних площин якщо
![]() (див. рис. 4.5)
(див. рис. 4.5)
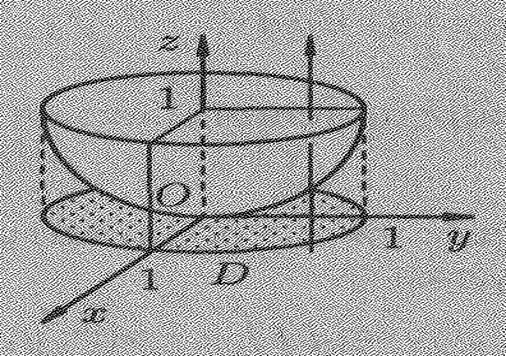
Рисунок 4.5
Рішення. Оскільки P(x,y,z)=xz, Q(x,y,z)=x![]() y, R(x,y,z)=y
y, R(x,y,z)=y![]() z,
z,
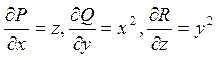 , то
, то
К = ![]() (z + x
(z + x![]() + y
+ y![]() )dx, dy.dz.
)dx, dy.dz.
Для обчислення потрійного інтеграла перейдемо до циліндричних координат: x=![]() . Якобіан відображення
дорівнює
. Якобіан відображення
дорівнює ![]() , тому
, тому
К=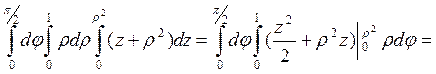
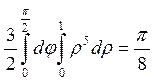
4.3.4 Дивергенція та ротор векторного поля
Візьмемо деяку
точку Р векторного поля ![]() , оточимо її замкненою поверхнею S, яка повністю знаходиться в полі.
Обчислимо потік вектора
, оточимо її замкненою поверхнею S, яка повністю знаходиться в полі.
Обчислимо потік вектора ![]() через поверхню S і розглянемо відношення цього потоку
до об'єму V області
через поверхню S і розглянемо відношення цього потоку
до об'єму V області ![]() , обмеженої поверхнею S
, обмеженої поверхнею S
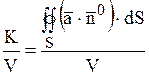 .
.
Знайдемо тепер межу відношення
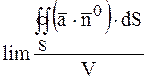 за умови, що область
за умови, що область ![]() стягується в точку Р, тобто що об'єм
стягується в точку Р, тобто що об'єм ![]() .
.
Дивергенцією
векторного поля ![]() в точці Р називається межа
відношення потоку вектора через поверхню, що оточує крапку Р, до об'єму,
обмеженого цією поверхнею, за умови, що вся поверхня стягується в точку Р.
в точці Р називається межа
відношення потоку вектора через поверхню, що оточує крапку Р, до об'єму,
обмеженого цією поверхнею, за умови, що вся поверхня стягується в точку Р.
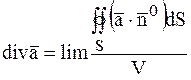 .
.
Теорема. Дивергенція векторного поля ![]() в точці Р виражається формулою
в точці Р виражається формулою ![]() , де частинні похідні
беруться в точці Р.
, де частинні похідні
беруться в точці Р.
Доведення. За формулою
Остроградського-Гауса 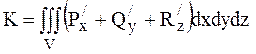 . Згідно теореми про середнє
потрійний інтеграл дорівнює добутку об'єму V на значення підінтегральної функції в
деякій точці
. Згідно теореми про середнє
потрійний інтеграл дорівнює добутку об'єму V на значення підінтегральної функції в
деякій точці ![]() області
області ![]() , тобто
, тобто
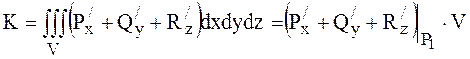 .
.
Якщо область ![]() стягується в точку Р, то точка
стягується в точку Р, то точка ![]() прямує до точки Р і тоді
прямує до точки Р і тоді
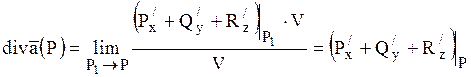 .
.
З визначення
дивергенції виходить, що якщо ![]() , то в точці Р – джерело, а якщо
, то в точці Р – джерело, а якщо ![]() , то в точці Р – стік.
, то в точці Р – стік.
Ротором векторного поля
![]() називається вектор
називається вектор
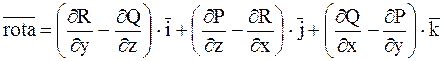 .
.
Для зручності
запам'ятовування ![]() зручно записувати в символічній
формі:
зручно записувати в символічній
формі:
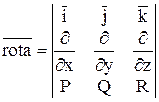 .
.
Цей визначник
розкривається за елементами першого рядка, при цьому операції множення
елементів другого рядка на елементи третього рядка розуміються як операції
диференціювання, наприклад 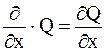 .
.
Приклад 4.5 Знайти ротор векторного поля
![]() .
.
Рішення.
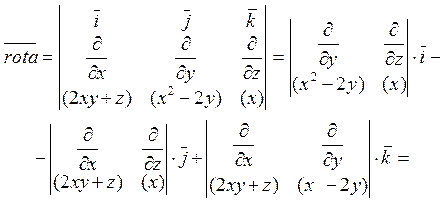
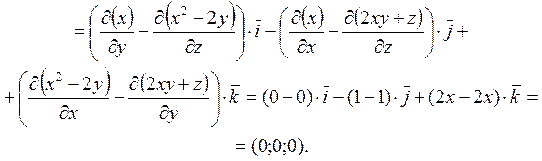
.
4.3.5 Потенціальне поле
Векторне
поле ![]() називається потенціальним, якщо
існує така функція
називається потенціальним, якщо
існує така функція ![]() , що у всіх точках, де поле задано,
виконується рівність:
, що у всіх точках, де поле задано,
виконується рівність:
![]() або
або ![]() ,
, 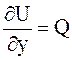 ,
, 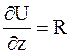 .
.
Функція U називається потенціалом векторного поля .
Для того, щоб
векторне поле, задане в однозв'язній області V вектором ![]() , було потенціальним,
необхідно і достатньо, щоб в кожній точці області, де задано поле, виконувалася
умова
, було потенціальним,
необхідно і достатньо, щоб в кожній точці області, де задано поле, виконувалася
умова ![]() .
.
Інакше кажучи, поле потенціальне, якщо виконуються рівності
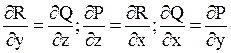 .
.
Якщо векторне
поле плоске, тобто ![]() , то воно потенціальне, якщо
, то воно потенціальне, якщо 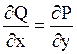 , оскільки в цьому випадку
, оскільки в цьому випадку 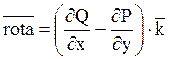 .
.
Якщо поле потенціальне, то криволінійні інтеграли, обчислювані вздовж кривих, що знаходяться в області, де задано це поле, не залежать від шляху інтеграції, а залежать тільки від початку і кінця руху по кривій. Це відбувається, оскільки умова потенціальності поля співпадає з умовою незалежності криволінійного інтеграла від шляху інтеграції.
Потенціал знаходимо за формулою
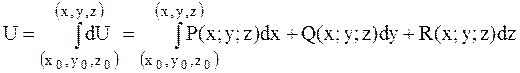 .
.
Потенціал поля
визначається неоднозначно, з точністю до постійного доданку, оскільки точка ![]() вибирається довільно.
Частіше в якості
вибирається довільно.
Частіше в якості ![]() беруть (0;0;0), якщо це точка, в
якій полі вектора
беруть (0;0;0), якщо це точка, в
якій полі вектора ![]() задано.
задано.
Приклад 4.6 Показати, що поле вектора ![]() потенціальне і знайти його
потенціал.
потенціальне і знайти його
потенціал.
Рішення.
Поле вектора ![]() буде потенціальним, якщо
буде потенціальним, якщо ![]() =0.
=0.
Знайдемо ![]() .
.
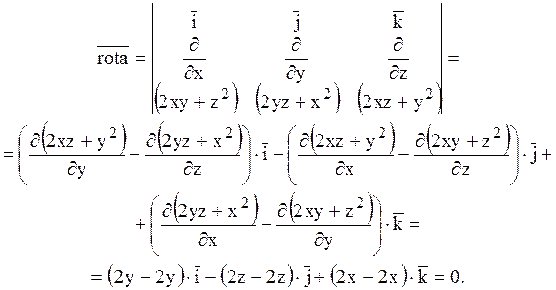
Оскільки ![]() =0, те поле вектора
=0, те поле вектора ![]() потенціальне. Знайдемо
потенціал
потенціальне. Знайдемо
потенціал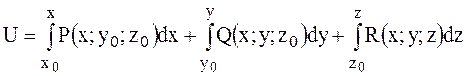 .
.
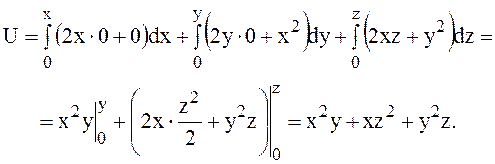
4.3.6 Циркуляція векторного поля
Циркуляцією вектора ![]() вздовж замкнутого контура L називається криволінійний інтеграл по
цьому контуру від скалярного добутку вектора
вздовж замкнутого контура L називається криволінійний інтеграл по
цьому контуру від скалярного добутку вектора ![]() на вектор
на вектор ![]() дотичної до контура:
дотичної до контура:
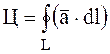 ,
,
якщо ![]() і
і ![]() , то
, то
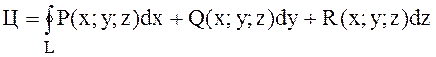
Додатним напрямом обходу замкненої кривої L вважають напрям, при якому область, обмежена цією кривою, залишатиметься зліва.
В силовому полі вищенаведена формула задає роботу при переміщенні матеріальної точки вздовж лінії L.
Приклад 4.7 Знайти циркуляцію векторного
поля ![]() уздовж кола x
уздовж кола x![]() +y
+y![]() =ax
=ax
Рішення.
Рівняння кола зведемо до параметричного вигляду з центром у точці (![]() ), тобто
), тобто
x=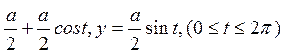 ;
;
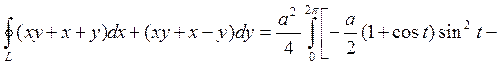
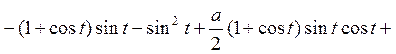
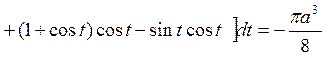 .
.
Формула Стокса. Нехай координати вектора ![]() безперервні і мають безперервні
частинні похідні, тоді циркуляцію вектора
безперервні і мають безперервні
частинні похідні, тоді циркуляцію вектора ![]() по замкненому контуру L зручно обчислити за формулою Стокса.
по замкненому контуру L зручно обчислити за формулою Стокса.
Теорема. Циркуляція вектора ![]() вздовж замкненого контура L дорівнює потоку ротора цього вектора
через будь-яку поверхню S, натягнуту на контур L.
вздовж замкненого контура L дорівнює потоку ротора цього вектора
через будь-яку поверхню S, натягнуту на контур L.
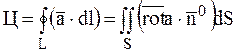 .
.
Передбачається,
що орієнтація нормалі ![]() до поверхні S злагоджена з орієнтацією контура L так, щоб з кінця нормалі
обхід контура у вибраному напрямі був видний таким, що скоюється проти
годинникової стрілки.
до поверхні S злагоджена з орієнтацією контура L так, щоб з кінця нормалі
обхід контура у вибраному напрямі був видний таким, що скоюється проти
годинникової стрілки.
З теореми виходить формула Стокса:
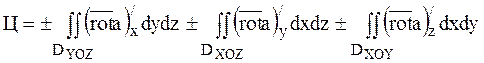 ,
,
де ![]() - проекції поверхні S на площині YOZ, XOZ, XOY.
- проекції поверхні S на площині YOZ, XOZ, XOY.
Окремим випадком
формули Стокса, коли поле вектора ![]() пласке, буде формула Гріна.
пласке, буде формула Гріна.
Якщо поле вектора
![]() плоске, то
плоске, то
![]() ,
,
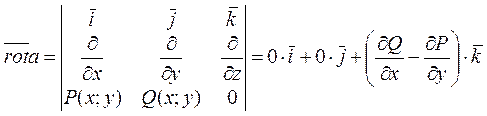 ,
,
оскільки ![]() =0 і
=0 і ![]() =0.
=0.
Тоді у формулі
Стокса ![]() =0 і
=0 і ![]() =0 і
=0 і
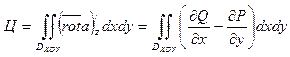 .
.
Приклад 4.8
Знайти циркуляцію вектора а =(5x+4y; 10x+3y) вздовж контура прямокутника, обмеженого лініями: x=0; y=0;x=2;y=3.
Рішення
Обчислимо інтеграл
Ц=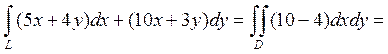
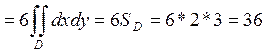 .
.
4.4 Оператор Гамільтона
Багато операцій векторного аналізу можуть бутизаписані в скороченій і зручній для розрахунків формі за допомогою символічного оператора Гамільтона «набла».
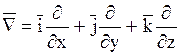 .
.
В цьому операторі
сполучені диференціальні і векторні властивості. Формальне множення ![]() на функцію U(x;y;z) розуміють як частинне
диференціювання
на функцію U(x;y;z) розуміють як частинне
диференціювання ![]() .
.
Правила дії з оператором «набла» такі:
1) Добуток набла – вектора ![]() на скалярну функцію U(x;y;z) дає градієнт цій функції:
на скалярну функцію U(x;y;z) дає градієнт цій функції:
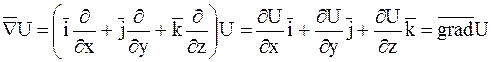 .
.
2) Скалярний добуток
набла - вектора ![]() на векторну функцію
на векторну функцію ![]() дає дивергенцію цієї
функції:
дає дивергенцію цієї
функції:
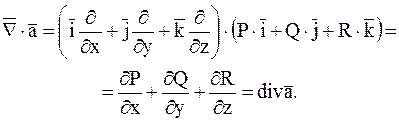
3) Векторний добуток
набла – вектора ![]() на векторну функцію
на векторну функцію ![]() дає ротор цієї функції:
дає ротор цієї функції:
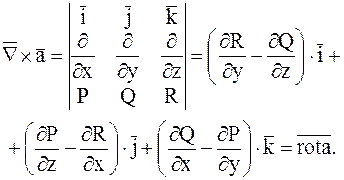
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.