Прямая задача теории погрешностей

Прямая задача теории погрешностей

Пусть  - дифференцируемая функция  аргументов, которые являются приближенными числами, абсолютная погрешность которых  достаточно мала. Прямая задача теории погрешностей заключается в вычислении предельной абсолютной и относительной погрешностей функции  при известной погрешности аргументов . Если  достаточно малы, то для вычисления погрешности справедливы формулы:    (1.6)                                           (1.7)

Следствие 1: Если , то из (6) следует, что за предельную абсолютную погрешность можно взять сумму абсолютных погрешностей слагаемых  (1.8)Следствие 2: Если все слагаемые одного знака, то из (7) следует, что – где  – максимальная из относительных погрешностей слагаемых. Следствие 3: Если , то из (7) следует, что за предельную относительную погрешность произведения можно взять сумму относительных погрешностей слагаемых:

            (1.9) Следствие 4: Если , то из (6) и (7) следует и .Замечание: Пусть , где  - близкие числа. Тогда  и для относительной погрешности получим . Так как знаменатель достаточно малое число, то относительная погрешность может резко возрасти, что приведет к потере точности. Поэтому следует избегать вычитания близких чисел. Обратная задача теории погрешностей Пусть нам нужно вычислить , где  - дифференцируемая функция аргументов . Обратная задача заключается в том, чтобы вычислить допустимые погрешности аргументов , с тем, чтобы погрешность вычисления функции  не превышала заданную величину. Для того, чтобы задача была математически определена необходимо наложить ограничения на поведение погрешностей аргументов.

1.  Принцип равных влияний. Пусть погрешности распределены так, что       выполняется условие       для любых  и . Из (6) получим

         ,    .           Откуда следует 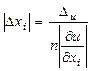                                                                                      (1.10)

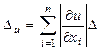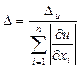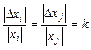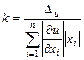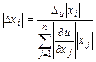2. Принцип равных абсолютных погрешностей. Пусть все аргументы имеют одинаковую абсолютную погрешность:  для любых  и . Тогда из (6) следует  и                                                     (1.11) 3. Принцип равных относительных погрешностей. Пусть  для любых  и . Тогда из (6) получим  ,                    откуда  и, следовательно, .                                             (1.12)

При решении обратной задачи все постоянные, которые не могут быть заданы точно, должны рассматриваться как приближенные.