М1 (х1, у2) і М2(х2, у2).
у = у0 + к (х – х0) (9) – рівняння прямої, яка проходить через точку М0(х0, у0) і має кутовий коефіцієнт к.
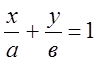 (10)
– рівняння прямої у відрізках на осях координат, де А(а, 0) і В(0, в)
– різні точки перетину прямої L з осями координат.
(10)
– рівняння прямої у відрізках на осях координат, де А(а, 0) і В(0, в)
– різні точки перетину прямої L з осями координат.
![]() (11)
– нормальне рівняння прямої, в якому р – довжина перпендикуляра до
прямої, опущеного з початку координат, a-
кут між цим перпендикуляром і віссю ОХ.
(11)
– нормальне рівняння прямої, в якому р – довжина перпендикуляра до
прямої, опущеного з початку координат, a-
кут між цим перпендикуляром і віссю ОХ.
Умови паралельності прямих (L1 || L2):
1) 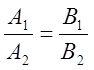 , де
, де ![]() ,
,
![]() вектори, перпендикулярні до прямих (L1 || L2).
вектори, перпендикулярні до прямих (L1 || L2).
2) 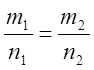 , де
, де ![]() ,
,
![]() - векторі, паралельні до прямих (L1 || L2).
- векторі, паралельні до прямих (L1 || L2).
3) к1 = к2, де к1 і к2 – кутові коефіцієнти прямих (L1 || L2).
Умови перпендикулярності прямих ![]() :
:
1) А1А2 + В1В2 = 0 ![]()
2) m1m2
+ n1n2 = 0 ![]()
3) ![]()
![]()
1) 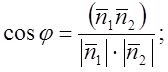 2)
2) 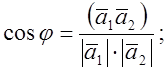 3)
3)
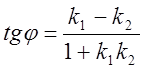
Відстань d від точки М*(х*, у*) до прямої, загальне рівняння якої (4) Ах + Ву + С = 0, можна знайти за формулою:
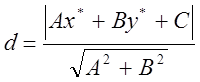 (11)
(11)
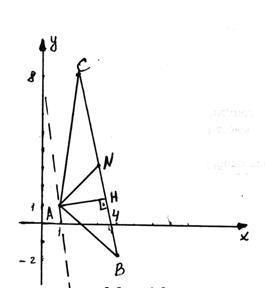
Приклади. Дано три вершини трикутника АВС А(1, 1), В(4, -2) і С(2, 8). (рис. 16)
1. Побудувати трикутник АВС в декартовій системі координат на площині ОХУ.
2. Знайти загальне рівняння прямої, на якої лежить медіана АN.
Розв’язання.
 Знайдемо
координати точки N– середини відрізка ВС за формулами
Знайдемо
координати точки N– середини відрізка ВС за формулами
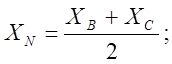
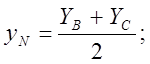 тобто
тобто
|
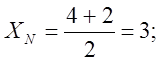
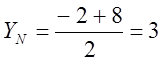 .
.
Таким чином, N(3, 3).
За двома точками знайдемо рівняння прямої АN:
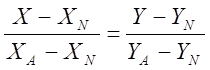 ,
,
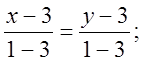 х = у, або
х = у, або
L1
![]() AN: х – у = 0.
AN: х – у = 0.
3. Знайти загальне рівняння прямої, на якої лежить сторона ВС трикутника АВС.
Розв’язання.
Знайдемо напрямний вектор ![]() прямої
ВС, тобто
прямої
ВС, тобто ![]() ,
, ![]() та
запишемо рівняння прямої у вигляді:
та
запишемо рівняння прямої у вигляді:
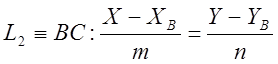 ,
, 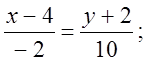
-5(х - 4) = у + 2, -5х – у + 18 = 0
![]()
4. Знайти рівняння прямої, на якої лежить висота АН трикутника АВС.
Розв’язання.
![]() - вектор
перпендикулярний до висоти трикутника АВС, проведеної через вершину А,
тобто
- вектор
перпендикулярний до висоти трикутника АВС, проведеної через вершину А,
тобто ![]() , тому
, тому
![]() -2х + 10у - 8 = 0
-2х + 10у - 8 = 0
![]()
5. Знайти рівняння прямої, яка проходить через точку А і паралельна до прямої ВС.
Розв’язання.
Оскільки напрямний вектор прямої ВС є вектор ![]() , то рівняння прямої L4можна записати у
вигляді:
, то рівняння прямої L4можна записати у
вигляді:
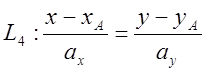 , або
, або 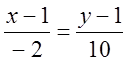
-5(х - 1) = у – 1
L4: 5x + у – 6 = 0
6. Знайти проекцію точки А на пряму ВС (координати точки Н).
Розв’язання.
Цією точкою є точка Н, яка знаходиться як точка перетину двох взаємно перпендикулярних прямих ВС і АН, тобто
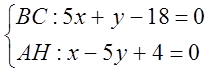
Розв’яжемо цю систему лінійних рівнянь за формулами Крамера.
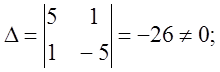
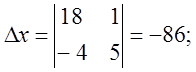
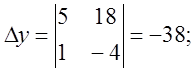
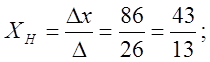
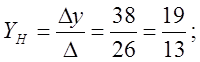
Одержимо, що проекція точки А на пряму ВС
є точка ![]() .
.
7. Знайти відстань точки А від прямої ВС.
Розв’язання.
Відстань точки d = АН знайдемо за формулою
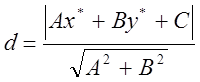 , тобто
, тобто
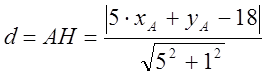 , оскільки рівняння прямої, на якої
лежать сторона ВС є рівняння
, оскільки рівняння прямої, на якої
лежать сторона ВС є рівняння
![]()
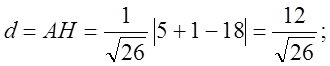
![]()
8. Знайти довжину висоти АН, як відстань між двома точками А і Н.
Розв’язання.
Відстань між двома точками d = АН знаходиться за формулою:
![]() , або
, або
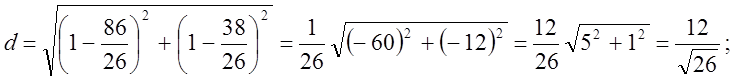
d = АН » 2,4
9. Знайти кут між прямими AN і АН.
Розв’язання.
Маємо ![]() - пряма, яка має
нормальний вектор
- пряма, яка має
нормальний вектор ![]() ,
,
![]() пряма, яка має
пряма, яка має ![]() .
.
Таким чином, 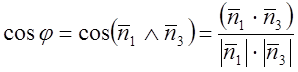 , або
, або
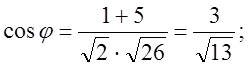
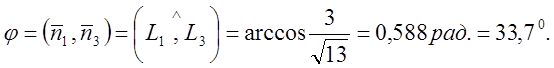
4.6 Криві другого порядку
Загальне рівняння кривої другого порядку в декартовій системі координат на площині ОХУ має вигляд:
Ах2 + Ву2 + Сху + Dх + Еу + F = 0 (1),
Де хоча б один з коефіцієнтів А, В, С відмінний від нуля, тобто використовується умова
А2 + В2 + С2 ¹ 0
Не обмежуючи спільності, можна вважати, що загальний вид рівняння другого степеня з двома змінними має п’ять членів, тобто С = 0. Розглянемо такі випадки:
1. ![]() - однакові знаки. Крива буде
еліпсом.
- однакові знаки. Крива буде
еліпсом.
2. ![]() - протилежні знаки. Крива буде
гіперболою.
- протилежні знаки. Крива буде
гіперболою.
3. ![]() , але А2 + В2
¹ 0. Крива є парабола.
, але А2 + В2
¹ 0. Крива є парабола.
В інших випадках рівняння (1) описує пару прямих (можливо таких, які збігаються), або уявну криву.
Наприклад, х2 + у2 = 0, х2 - у2 = 0.
Означення 1. Еліпсом називається геометричне місце точок площини, сума відстаней яких від двох фіксованих точок F1 і F2площини, що називаються фокусами, є величина стала, тобто
F1M + F2M = 2а (1),
де М – довільна точка еліпсу, а = const (див. рис. 17.)
Введемо на площині декартову систему координат так, щоб координати фокусів еліпса відносно цієї системи були F1(-с, 0) і F2(с, 0). Позначивши довільну точку еліпса через М(х, у), можна одержати канонічне рівняння еліпса:
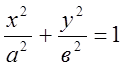 , де
, де ![]() (2)
(2)
Означення 2. Ексцентриситетом еліпса називається відношення відстані між фокусами цього еліпса до довжини його більшої осі (2а), тобто
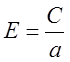 (3)
(3)
Оскільки с < а, то Е < 1. У випадку кола в = а, Е = 0 (х2 + у2 = а2)
Таким чином, ![]() і характеризує форму
еліпса.
і характеризує форму
еліпса.
Означення 3. Директрисами називаються дві прямі, перпендикулярні
до більшої осі еліпса і розташовані симетрично відносно центра на відстані ![]() від нього.
від нього.
Рівняння їх у вибраній системі координат мають вигляд
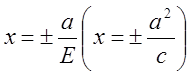 (4)
(4)
Означення 4. Гіперболою називається геометричне місце точок площини, для яких абсолютна величина різниці відстаней до двох фіксованих точок F1 і F2 площини, що називаються фокусами, є величина стала, тобто
![]() (5) (див. рис.
18)
(5) (див. рис.
18)
Канонічне рівняння гіперболи в декартовій системі координат ОХУ має вигляд
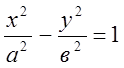 , де
, де ![]() (6)
(6)
Ексцентриситет гіперболи також характеризує форму її та знаходиться за формулою
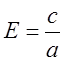 .
.
У цьому випадку стала величина 2а називається
дійсною віссю гіперболи. Оскільки ![]() , то
, то ![]() .
.
У випадку равностороньої гіперболи а = в, ![]()
Означення 5. Асимптотами гіперболи називаються дві прямі, до яких
прямують вітки гіперболи при ![]() . Вони є діагоналями
прямокутника, сторони якого дорівнюють 2а і 2в, тобто мають рівняння
. Вони є діагоналями
прямокутника, сторони якого дорівнюють 2а і 2в, тобто мають рівняння
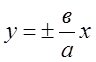 (8)
(8)
Означення 6. Директрисами гіперболи називаються дві прямі,
перпендикулярні до дійсної осі гіперболи (яка її перетинає) і розташовані
симетрично відносно центра на відстані ![]() від
нього.
від
нього.
Рівняння їх мають вигляд:
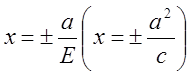 (9)
(9)
Гіпербола має вигляд кривої, зображеної на рис. 19.
Означення 7. Параболою називається геометричне місце точок площини, рівновіддалених від фіксованої точки F, що називається фокусом, і фіксованої прямої, яка називається директрисою.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.