Розробка плану вибіркового контролю якості виробів РЕА та МЕА по кількісним характеристикам, страница 3

Из анализа приведенных формул нетрудно заметить, что вследствие асимметрии распределения при α_i ≠ 0 и изменившегося рассеивания k_i ≠ 1 планы контроля для верхней и нижней границы отличаются как по объему выборки, так и по оперативным характеристикам. Объемы выборок вычисляются по формулам[2]:

для верхней границы

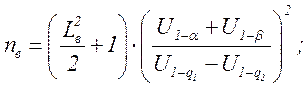                                                (3.15)

для нижней границы

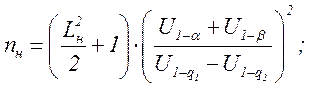                                                (3.16)

Для построения оперативных характеристик предварительно вычисляют для каждой границы отдельно[2]:

для верхней

                                                            (3.17)

для нижней

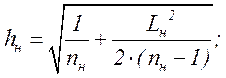                                                            (3.18)

Вычисленные характеристики позволят для каждой границы допуска отдельно построить оперативные характеристики, рассчитать предельные отклонения контролируемых параметров и сопоставить их и критериями приемки. Для односторонних допусков строят одну оперативную характеристику и используют один соответствующий критерий приемки.

4 РАСЧЕТ ПОКАЗАТЕДЕЙ ПРИЕМОЧНОГО КОНТРОЛЯ

Задание.

Рассчитать оперативные характеристики и планы приемочного контроля для партии напыленных на ситалловую подложку резисторов с омическим сопротивлением 10 Ом  ± 10%. Принять решение о приемке или забраковании партии резисторов.

Задание выполняется в следующем порядке:

1. Вариант задания устанавливается преподавателем по Таблице П.2 приложения вариант № 19.

2. В соответствии с заданным вариантом планы контроля должны удовлетворять следующим требованиям:  q₁ = 0,005; q₂ = 0,05; α = 0,15; β = 0,15. По данным технических условий для контролируемой партии изделий устанавливаем следующие характеристики:

а) номинал исследуемого параметра N(y) = 10 Ом;

б) верхняя граница допуска  y_в = 11 Ом;

в) нижняя граница допуска y _н= 9 Ом;

г) среднеквадратическое отклонение σ(y)_ту = 0,33 Ом.

3. Рассчитываем приемочный критерий Т по формуле (3.1):

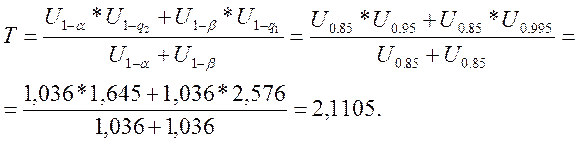
4. Находим объем выборки по формуле (3.2):

.

Таким образом, объем выборки – 16.

5. Для расчета координат точек оперативной характеристики вычисляем величину   по формуле (3.3):

.

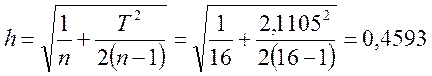Последующие расчеты, необходимые для построения оперативной характеристики, вводим в таблицу 4.1.

Таблица 4.1

№	Р	Up	h*Up	Kq = T – h∙Up	Pт	q = 1- Pт
1	0,95	-1,645	-0,756	2,867	0,9979	0,0021
2	0,85	-1,036	-0,476	2,587	0,9951	0,0049
3	0,68	-0,468	-0,215	2,326	0,99	0,01
4	0,5	0	0	2,1105	0,9821	0,0179
5	0,3	0,524	0,241	1,870	0,9692	0,0308
6	0,15	1,036	0,476	1,635	0,9489	0,0511
7	0,1	1,282	0,589	1,522	0,9358	0,0642

При заполнении таблицы 4.1 в столбце 5 используется линейная интерполяция, так как в данном случае оправдано допущение о пропорциональности приращения функции при изменении аргумента. Если заданное значение аргумента ( в нашем случае K_q = U_p) лежит между помещенными в табл. П.3[2] значениями U_p0  и U_p1 = U_p0 + l, которым соответствуют значения функции Р₀ = f(U_p) и Р₁ = f(U_p1) = Р₀ + Δ, то при линейной интерполяции принимают вид[2]:

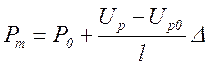,                                                      (4.1)

где Р_т – искомая вероятность, соответствующая аргументу  K_q = U_p ;

      Р₀  -  ближайшее меньшее по сравнению с искомым значением  Р_т значение вероятности, взятое из табл. П.3[2];

U_p – принимается равной K_q , взятой из столбца 4 табл. 4.1;

 U_p0 – ближайшее меньшее по сравнению с U_p значение аргумента, взятое из табл. П.3[2];

     l – разность между ближайшим большим U_p1 и меньшим U_p0  значениями аргумента, между которыми заключено значение K_q = U_p , т.е.  l = U_p1 - U_p0 ; Δ – разность между ближайшим большим Р₁ и  меньшим Р₀ значениями функции, между которыми заключено искомое значение Р_т , т. е. Δ = Р₁ -  Р_0.

В нашем примере первому значению K_q = 2,867, взятому из табл. 4.1, соответствует ближайшее значение из графы U_p табл. П.3[2], U_p0 = 2,807 и

U_p1 = 2,878 откуда l = 0,071. Соответствующие им значения функции принимают вид: Р₀ = 0,9975 и Р₁ = 0,9980, что соответствует Δ = 0,0005.

Таким образом, искомое значение Р_т  находим после подстановки соответствующих величин в формулу (4.1):

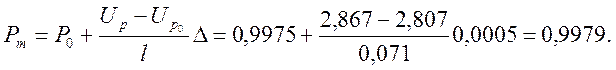
По данным таблицы 4.1 строятся оперативные характеристики 100%-ного и выборочного контроля. График оперативной характеристики представлен на рис. 4.1(см. с. 15).

6. Максимальную дисперсию σ_max рассчитываем по формуле[2]:

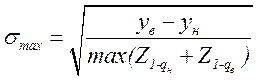,                                            (4.2)

где q_н = q_в = q_к = 0,0179 (из таблицы 4.1 для Р = 0,5);

  (из табл. П.3[2], графа для  при значении

Р = 1 - q_к=0,9821).

Подставляя эти данные и требования ТУ в последнюю формулу(4.2), получаем:

.

7. По результатам обработки статистических данных вносим в отчет по данной работе основные характеристики эмпирического распределения:

а) среднее значение контролируемого параметра  = 10,285 Ом;

б) среднеквадратическое отклонение от среднего s(y) = 0,298 Ом;