Векторне поле називають потенціальним ![]() (М)
в області V ,якщо існує
така однозначна скалярна функція
(М)
в області V ,якщо існує
така однозначна скалярна функція![]() , задана вV ,
що в усіх точках цієї області
, задана вV ,
що в усіх точках цієї області
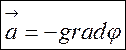 .
(3.1)
.
(3.1)
Функцію ![]() називають
скалярним потенціалом векторного поля
називають
скалярним потенціалом векторного поля![]() (М)
. Потрібно відзначити , що векторний потенціал визначається з точністю до
деякої сталої, в цьому можна переконатися, розглянувши скалярний потенціал
(М)
. Потрібно відзначити , що векторний потенціал визначається з точністю до
деякої сталої, в цьому можна переконатися, розглянувши скалярний потенціал ![]() підставити його у формулу (3.1).
підставити його у формулу (3.1).
Критерій потенціальності поля
Необхідною і достатньою умовою того, щоб в
однозв’язній області векторне поле ![]() було
потенціальним, є виконання в усіх точках області рівності
було
потенціальним, є виконання в усіх точках області рівності
![]() =0.
(3.2)
=0.
(3.2)
В необхідності умови (3.2) легко переконатися
безпосереднім обчисленням. Справді, якщо поле ![]() потенціальне,
то за означенням
потенціальне,
то за означенням ![]() і
і
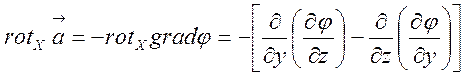 .
.
Аналогічно переконуємось, що ![]() і
і ![]() .
.
Достатність умови можна встановити так. Якщо облась V поля однозв’язна і C– довільний замкнений контур у полі, то завжди можна „натягнути” на контур Cдеяку поверхню Sтак, щоб вона цілком лежала в області V. В такому разі для довільного замкнутого контура C і обмеженої ним поверхні S за формулою Стокса () та з умови (3.2) випливає, що
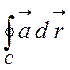 =0,
=0,
тобто циркуляція вектора поля по довільному замкненому контуру C в однозв’язній області V дорівнює нулю.
Соленоїдальне (трубчасте) векторне поле
Векторне поле ![]() (М)
називають соленоїдальним в області V, якщо існує інше таке векторне поле
(М)
називають соленоїдальним в області V, якщо існує інше таке векторне поле ![]() , задане в області V, в усіх точках якої
, задане в області V, в усіх точках якої
![]() =
=![]() .
(3.3)
.
(3.3)
Функцію ![]() називають
векторним потенціалом поля
називають
векторним потенціалом поля ![]() . Векторний
потенціал поля визначається з точністю до градієнта, в чому можна переконатися
безпосереднім обчисленням.
. Векторний
потенціал поля визначається з точністю до градієнта, в чому можна переконатися
безпосереднім обчисленням.
Необхідною і достатньою умовою соленоїдальності поля є рівність нулю його дивергенції, тобто виконання в усіх точках області умови
![]() =0.
(3.4)
=0.
(3.4)
Необхідність умови перевіряється безпосередньо.
На основі (3.3) і (3.4) маємо:
![]() =
=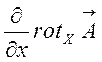 +
+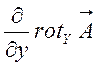 +
+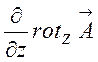 =
=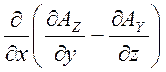 +
+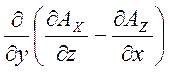 +
+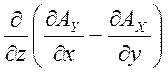 ==0,
==0,
бо всі похідні взаємно знищуються.
Достатність умови (3.4) обґрунтовується
безпосередньою побудовою векторного потенціалу ![]() .
.
Лапласівське (гармонічне) векторне поле
Векторне поле ![]() називають
лапласівським, якщо в кожній точці області справджуються рівності
називають
лапласівським, якщо в кожній точці області справджуються рівності
![]()
![]() ,
(3.5)
,
(3.5)
![]() .
(3.6)
.
(3.6)
Отже, лапласівське поле є водночас потенціальним і соленоїдальним.
З умови (3.5) випливає, що існує скалярний потенціал ![]() поля, тобто
поля, тобто
![]() .
.
Підстановка цього виразу для ![]() в (3.6) дає
в (3.6) дає
![]() ,
,
або
![]() .
(3.7)
.
(3.7)
Отже, лапласівське поле в однозв’язній області цілком визначається скалярним потенціалом ![]() ,
який задовольняє рівняння (3.7).
,
який задовольняє рівняння (3.7).
Основна задача векторного аналізу
Основна задача векторного анлізу формулюється
так: знайти в певній області поле ![]() ,якщо в ній задано
,якщо в ній задано
![]() і
і ![]() .
.
Точніше, вважається, що в кожній точці Р певної області V справджуються рівності
![]()
![]() =
=![]() ,
,
![]() =
=![]() .
(4.1)
.
(4.1)
Тут ![]() і
і ![]() - задані в області V і неперервні в ній функції (крім того функція
- задані в області V і неперервні в ній функції (крім того функція ![]() повинна
задовольняти умову
повинна
задовольняти умову ![]() , тому що
, тому що ![]() ).
).
В курсі диференціальних рівнянь доводиться, що система (4.1) має частинний розв’язок такого вигляду:
![]() =
=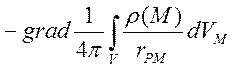 +
+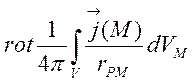 ,
(4.2)
,
(4.2)
де М – біжуча точка області V; Р – точка, в якій визначаємо вектор поля; rPM – віддаль між точками Р і М; dVM – елемент об’єму в точці М ; ![]() і
і ![]() -
значення функції в точці М .
-
значення функції в точці М .
Загальний розв’язок системи (4.1) матимемо, коли до частинного розв’язку (4.2) додамо загальний розв’язок однорідної системи
![]()
![]() ,
,
![]() .
(4.3)
.
(4.3)
Було показано, що система (4.3) визначає гармонічне (лапласівське) поле. Отже, загальний розв’язок неоднорідної системи (4.1) дістанемо, додавши до (4.2) довільне гармонічне поле
![]() =
=![]() +
+![]() ,
(4.4)
,
(4.4)
де ![]() - частиний розв’язок
(4.2), а
- частиний розв’язок
(4.2), а ![]() - довільне гармонічне поле.
- довільне гармонічне поле.
У фізичних застосуваннях найчастіше буває,
коли шукане поле ![]() розглядається в усьому
просторі і до того ж воно рівномірно спадає до нуля при необмеженому віддаленні
точки Р в нескінченність. Щодо функцій
розглядається в усьому
просторі і до того ж воно рівномірно спадає до нуля при необмеженому віддаленні
точки Р в нескінченність. Щодо функцій ![]() і
і
![]() , то вони повинні бути відміні від
нуля тільки в скінченній частині простору. За цих умов гармонічне поле
, то вони повинні бути відміні від
нуля тільки в скінченній частині простору. За цих умов гармонічне поле ![]() , як виявляється, тотожно дорівнює
нулю і тому відповідний єдиний розв’язок задачі подається тільки формулою
(4.2).
, як виявляється, тотожно дорівнює
нулю і тому відповідний єдиний розв’язок задачі подається тільки формулою
(4.2).
Отже, в звичайних фізичних застосуваннях:
1)
векторне поле ![]() однозначно визначається в усьому
просторі за формулою
однозначно визначається в усьому
просторі за формулою
![]() =
=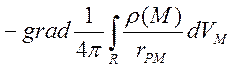 +
+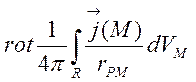 ,
(4.5)
,
(4.5)
деR – весь
простір, а функції ![]() і
і ![]() відмінні від нуля лише в скінченній частині простору
(тут
відмінні від нуля лише в скінченній частині простору
(тут ![]() ,
, ![]() );
);
2)
якщо поле ![]() має джерела
має джерела ![]() ,
тоді як густина циркуляції
,
тоді як густина циркуляції ![]() рівна нулю, то
рівна нулю, то ![]() визначається
за формулою
визначається
за формулою
![]() =
=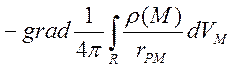 ,
(4.6)
,
(4.6)
отже, в цьому випадку поле потенціальне; його цого скалярний потенціал дорівнює
![]() =
= ;
(4.7)
;
(4.7)
3)
якщо густина циркуляції ![]() відміна від нуля, а густина джерел
відміна від нуля, а густина джерел ![]() дорівнює нулю, то з (4.5) знаходимо
дорівнює нулю, то з (4.5) знаходимо
![]() =
=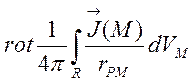 ,
(4.8)
,
(4.8)
тобто поле вектора ![]() соленоїдальне;
його векторний потенціал дорівнює
соленоїдальне;
його векторний потенціал дорівнює
![]() =
=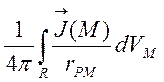 .
(4.9)
.
(4.9)
Диференціальні операції другого порядку
Розглянемо диференціальні операції, які
дістають двократним застосуванням оператора ![]() .
Можна утворити тільки п’ять таких диференціальних операцій другого
порядку:
.
Можна утворити тільки п’ять таких диференціальних операцій другого
порядку:
|
Операції першого порядку |
|
|
|
||
|
Операції другого порядку |
|
|
|
|
|
Дві з них, як раніше було з’ясовано, дають тотожний нуль:
1. ![]() =0
(потенціальне поле безвихрове);
=0
(потенціальне поле безвихрове);
2. ![]() =0 (вихрове
поле соленоїдальне).
=0 (вихрове
поле соленоїдальне).
Вираз ![]() є
вже відомий оператор Лапласа (1.18)
є
вже відомий оператор Лапласа (1.18) ![]() .
.
Обчислимо ![]() =
=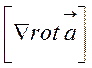 =
=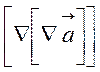 .
.
Використовуючи формулу векторної алгебри для
подвоєного векторного добутку 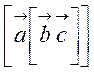 =
=![]() -
-![]() ,
знайдемо
,
знайдемо
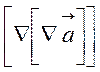 =
=![]() -
-![]() .
.
Тому маємо
![]() =
=![]() -
-![]() =
=![]()
![]() -
- ![]() .
.
Остаточно знаходимо
![]() =
=![]() -
-
![]() . (5.1)
. (5.1)
де ![]() - оператор
Лапласа.
- оператор
Лапласа.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.