|
|
|
|
|
Позначимо |
і знайдемо
При рішенні прикладів 1 і 2 суму арксинусів можна виразити не тільки через арксинус, а і через будь-яку іншу зворотну тригоно-
|
|
|
|
|
|
|
Звідси |
|
Позначимо |
|
і знайдемо |
|
|
|
|
метричну функцію. Дійсно, при відповідно маємо
|
|
|
|
|
|
|
|
|
|
|
|
|
, виходить, |
|
Оскільки |
|
Тому що |
Звідси знаходимо
Тоді
або
одержуємо
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
або |
|
Отже, |
|
2. Знайти суму |
|
і знайдемо |
|
Позначимо |
|
при |
|
|
Звідси
|
|
|
виходить, |
|
|
|
|
Оскільки
З огляду на цю умову, при п = I (інші значення не удовлетвори-ют умові) знаходимо
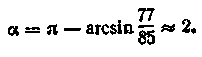
По цій формулі в прикладі
а в прикладі 2
Аналогічно, для суми
з огляду на, що
|
|
і позначаючи
|
відкіля |
або
1 одержуємо
одержуємо
|
|
Застосовуючи формулу (15.4) до лівої частини цієї рівності, знаходимо
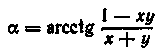
або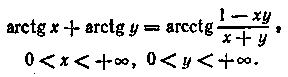
3. Знайти суму![]()
Використовуючи попередню формулу, записуємо
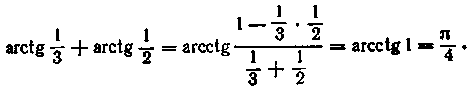
4. Знайти різниця arccos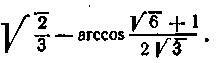
Позначимо
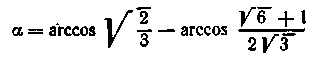
і знайдемо
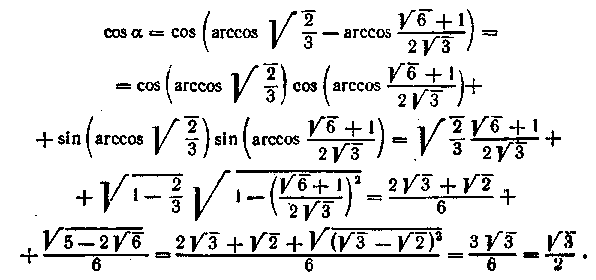
Виходить,
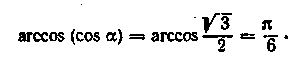 'Ч
'Ч
І- І Оскільки 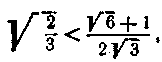 те і
те і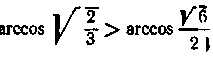
Тоді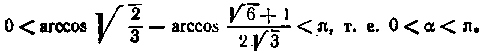
Застосовуючи до лівої частини рівності (1) формулу (15.2), одержуємо а = -
IIIIИ
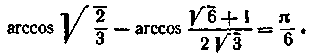
б.
Обчислити![]() ho формулі (15.11) з обліком того, що
ho формулі (15.11) з обліком того, що![]() одержуємо
одержуємо
;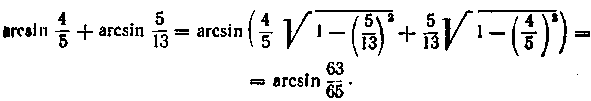
Аналогічно складаємо
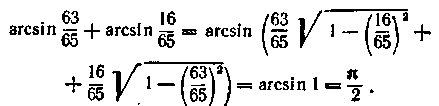
6.
Довести,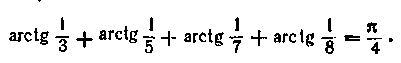 що По формулі (15.15) з обліком того, що
що По формулі (15.15) з обліком того, що ![]() знаходимо суму
знаходимо суму
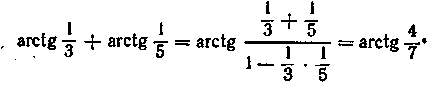
Аналогічно складаємо
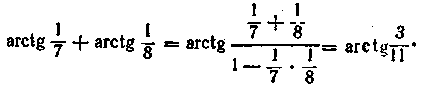
З огляду на, що 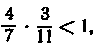 одержуємо
одержуємо
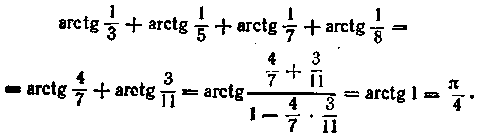
15.5. Формули подвоєння зворотних тригонометричних функцій і розподілу їх на два
Приведемо формули подвоєння зворотних тригонометричних функцій:
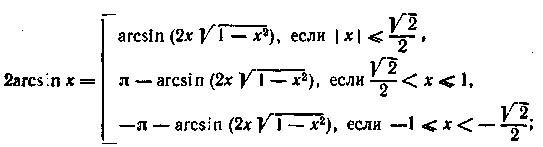 (15.17)
(15.17)
![]() (15.18)
(15.18) 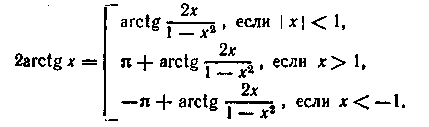 (15.19)
(15.19)
Формули розподілу зворотних тригонометричних функцій на два мають вигляд
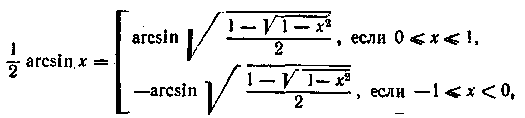 (15.20)
(15.20)
![]() (15.21)
(15.21) 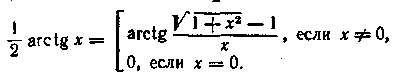 (15.22)
(15.22)
Розглянемо приклади.
1. Обчислити![]()
По формулі (15.17) з
обліком того, що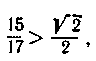 знаходимо
знаходимо
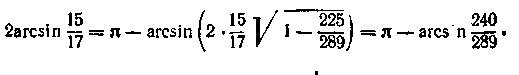
2. Обчислити![]()
По формулі (15.19) з обліком того, що —2<—1, знаходимо
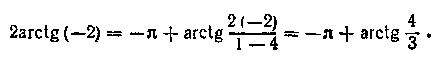 !
!
З огляду на,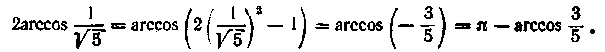 що
що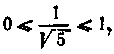 по формулі
(15.18) одержуємо
по формулі
(15.18) одержуємо
Тоді
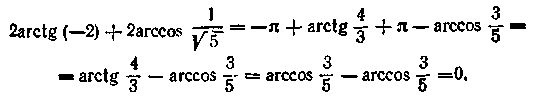
3. Обчислити![]() Застосовуючи
формулу (15.19), знаходимо
Застосовуючи
формулу (15.19), знаходимо
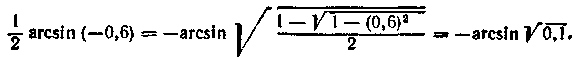
15.6. Тотожні перетворення
с зворотними тригонометричними функціями
Приведемо приклади виконання тотожних перетворень виражень, що містять зворотні тригонометричні функції.
1. Обчислити
Знайдемо![]()
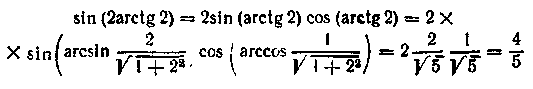 /
/
і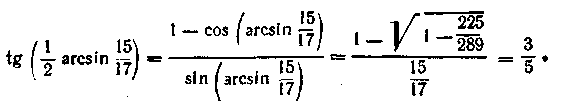
Тоді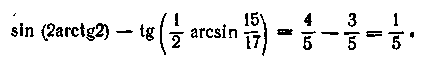
2. Обчислити
Виконаємо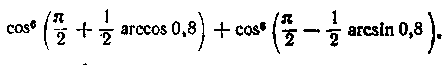 перетворення:
перетворення:
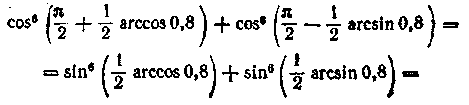
|
|
|
|
|
|
|
|
|
а права |
|
те рівняння може |
|
З огляду на, що |
|
Тоді рівняння мо- |
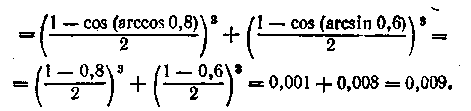
3. Довести,
що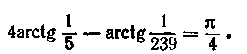
По формулі (15.17) знаходимо
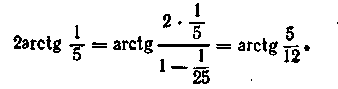
Аналогічно
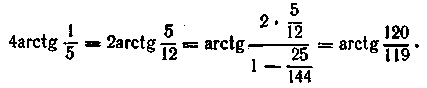
За допомогою формули (15.16) знаходимо
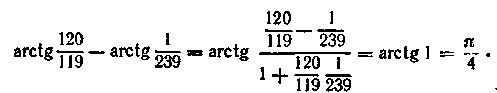
4. Довести, що
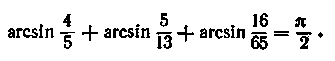
По формулі (15.11) знаходимо
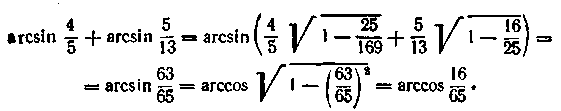
Використовуючи тотожність (15.9), одержуємо
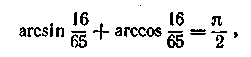
т. е,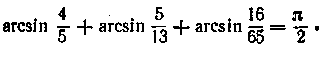
15.7. Рішення рівнянь і нерівностей, що містять зворотні тригонометричні функції
Приведемо приклади рішення рівнянь і нерівностей зі зворотними тригонометричними функціями.
1, Вирішити рівняння ![]() І
І
|
|
Оскільки дане рівняння визначене при
частина його обмежена:
|
|
мати рішення, що належать інтервалові
|
|
Якщо аргументи рівні, то синуси їх також рівні, т. е,
|
|
відкіля одержуємо
|
|
Вирішуючи це рівняння, знаходимо
|
|
2. Вирішити рівняння
Якщо аргументи рівні, то і їхніх тангенсах рівні:
![]()
З цього вираження одержуємо
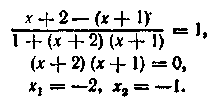
|
|
3. Вирішити рівняння
|
|
|
|
|
одержуємо |
|
жет мати рішення, якщо |
|
|
|
Виходить, |
|
|
|
або |
|
|
|
По формулі (15.5) одержуємо |
Рівняння визначене при
З огляду на, що рішенням рівняння може бути тільки негативне \ значення х, знаходимо
![]()
або
![]()
відкіля
![]()
Узявши косинус від обох частин рівняння, одержимо
![]()
або![]()
Після зведення обох частин рівняння в квадрат і спрощень знаходимо
![]()
отже,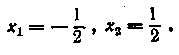 Значення
Значення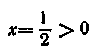 не є
не є
рішенням рівняння. Тому
![]()
4.
Вирішити рівняння і Представимо рівняння![]() у виді
у виді
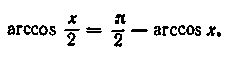
Застосовуючи до правої частини цього рівняння формулу (15.9), одержуємо
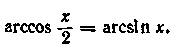
Тому що ![]() те рішеннями можуть бути тільки ті значення х,
те рішеннями можуть бути тільки ті значення х,
при яких ![]() Тоді по формулі
(15,5)
Тоді по формулі
(15,5)
приведене рівняння можна записати у виді
![]()
^відкіля випливає,
що![]()
Ііосле зведення обох частин цього рівняння в квадрат одержуємо
![]()
або
![]()
ґ Значення![]() не є
рішенням рівняння. Тому
не є
рішенням рівняння. Тому
^год![]()
5. Вирішити нерівність![]()
Застосовуючи формулу (15.9), одержуємо
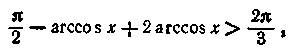
відкіля випливає, що![]() або
або
![]()
Узявши косинус від обох частин подвійної нерівності і
врахувавши, що cos* на розглянутому інтервалі убуває, знайдемо або![]()
![]()
6. Вирішити неравенствоДанное нерівність
визначена при умовах![]()
або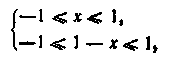
![]()
Звідси знаходимо![]()
Оскільки арксинус — функція зростаюча, та дана нерівність рівносильна нерівності
![]()
|
|
|
|
|
З урахуванням області визначення знаходимо |
Виходить,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.