Вирази та їх перетворення, страница 32

Безсумнівно, що вчителю корисно бути ознайомленим з різними побудовами шкільного вчення про дійсні числа, які в деякій мірі висвітлюють ідеї, що лежать в основі відповідних наукових побудов  теорії дійсних чисел.

Вводити дійсні числа можна за відомою учням схемою. Числа натуральні, нуль і протилежні натуральним становлять множину цілих чисел. Числа цілі і дробові становлять множину раціональних чисел. Аналогічно: числа раціональні і ірраціональні становлять множину дійсних чисел. Сказане бажано ілюструвати конкретними прикладами і за допомогою схеми:

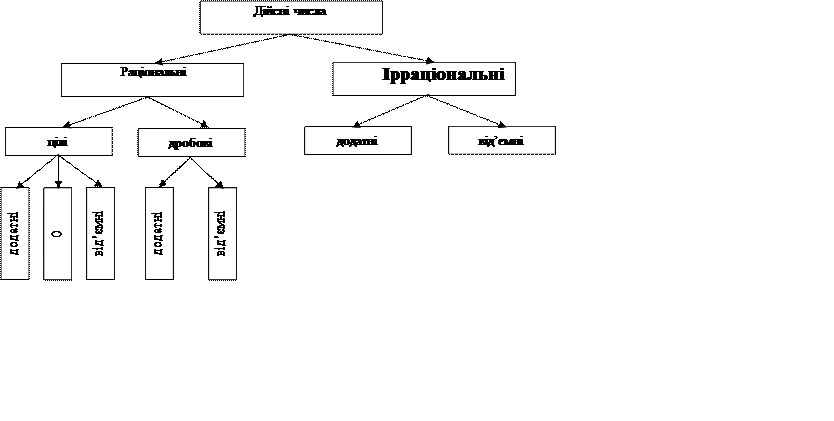
Отже, якщо множину раціональних чисел доповнити числами ірраціональними, то одержана розширена множина називається множиною дійсних чисел і позначається буквою . У множині дійсних чисел виявилась можливою дія добування коренів з раціональних чисел і деякі інші математичні операції . оскільки дійсні числа записуються у вигляді нескінчених десяткових дробів (періодичних, або неперіодичних), то їх можна порівняти за тими ж  самими правилами, що й десяткові дроби.

Введення раціональних чисел показало, що на  координатній прямій є точки, яким не відповідає жодне раціональне число. Після введення раціональних чисел  і утворення множини  дійсних чисел виконується взаємно означена відповідність між множиною точок координатної прямої і множиною дійсних чисел. Це означає, що кожній точці координатної прямої відповідає дійсне число (її координата), і навпаки, кожному дійсному числу відповідає точка на координатній прямій.

Як уже зазначалося, строга теорія дійсних чисел досить складна. Тому учням 8 класу дають лише спрощені уявлення про цю множину. Щодо виконання чотирьох арифметичних дій над дійсними числами, то учням досить сказати, що в цій множині виконуються всі арифметичні дії, крім ділення на нуль. В результаті діставатимемо  кожного разу дійсні числа. Тільки коли хоча б одне з чисел є ірраціональним, виконують дії над їхніми наближеними значеннями, взявши попередньо ці наближення з однаковою кількістю десяткових знаків. Наприклад, якщо треба додати  і , пишуть:

Аналогічно можна знайти наближене значення різниці, добутку, частки даних чисел з якою завгодно точністю. Для цього треба мати наближені значення компонентів з достатньою точністю.

Корисно звернути увагу учнів, що в окремих випадках сума (різниця, добуток частка) двох ірраціональних чисел може бути число раціональним. Але якщо одне число раціональне, а друге ірраціональне, то їх сума і різниця завжди ірраціональні. Переконатись у цьому можна методом від супротивного, враховуючи, що ніяке ірраціональне число не дорівнює раціональному.

Зрозуміло, що такий вигляд розглядуваної теми далекий від строгого. Але строга теорія дійсних чисел  досить складна; не входить в програму середньої школи.

 Практичне заняття

Тема: Вирази та їх перетворення.

План

       1.Вивчення тотожних перетворень цілих виразів

2. Тотожні перетворення раціональних виразів

3. Тотожні перетворення ірраціональних виразів

1.Вивчення тотожних перетворень цілих виразів.

Перетворення в курсі алгебри розподіляються на два класи: 1) тотожні перетворення – перетворення виразів; 2) рівносильні перетворення – перетворення формул. У випадку, коли виникає потреба у спрощені однієї частини формули, в ній виділяється вираз, який перетворюється (використовується певне тотожне перетворення). Наприклад ; .

Шкільна практика свідчить про те, що при вивченні різних видів тотожних перетворень доцільним виявляється алгоритмічний підхід. Це означає, що вивчення кожного з видів перетворень має завершуватись (або починатись) формулюванням правила (алгоритму) перетворення.

Основна мета виконання тотожних перетворень цілих виразів, як уже зазначалося, полягає у поданні їх у вигляді одночлена чи многочлена стандартного вигляду. Мотивується це перетворення потребою спрощення одночлена, одержаного при множенні, утворенні добутку двох одночленів. Дана цільова установка має бути усвідомлена учнями, що надасть їх діяльності осмисленості і цілеспрямованості. У зв’язку з цим необхідно забезпечити сформованість у школярів понять одночлена і многочлена та їх стандартного вигляду. Можливо при цьому підкреслити теоретичну основу виконання:  у разі зведення одночлена до стандартного вигляду використовується переставний, сполучний закони множення і правило множення степенів з однаковою основою.

Практика показує, що немає потреби формулювати строге означення одночлена та його стандартного вигляду. Зміст цих понять, як і поняття многочлена стандартного вигляду, повно і однозначно розкривається на конкретних прикладах описово. Многочлени, природно, означають як суму одночленів. Але алгоритм виконання таких перетворень, як зведення одночлена чи многочлена до стандартного вигляду повинен бути чітко сформульований. Зокрема, щоб привести одночлен до стандартного вигляду, треба перемножити числові множники і степені змінних з однією основою; одержане число поставити в добутку на першому місці. Щоб звести до стандартного вигляду многочлен, треба усі одночлени, з яких він складається, подати у стандартному вигляді і звести подібні члени. Паралельно із зведенням одночлена до стандартного вигляду розглядається важливе поняття коефіцієнта. Поняття це на перший погляд досить просте, але практика свідчить, що учні досить часто неправильно визначають коефіцієнти у випадках, коли вони дорівнюють 1 та –1, що призводить до грубих помилок при виконанні тотожних перетворень, розв’язуванні рівнянь тощо. Хоч перші відомості про коефіцієнт учні дістали у попередньому класі, про те саме тут, при зведенні одночленів до стандартного вигляду, є сприятливі можливості для попередження подібних помилок. При цьому мало обмежитися лише виглядом вправ виду: назвіть коефіцієнти в одночленах  ,  та ін. Корисно, щоб учні побачили ці коефіцієнти в процесі їх утворення. Ефективними  у зв’язку з цим виявляються вправи такого змісту : визначте коефіцієнти у виразах:

; ; .

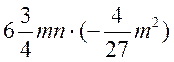Зведення одночлена до стандартного вигляду лежить в основі дії множення одночленів.